2013-2014 Bahar
ULUDAĞ ÜNİVERSİTESİ
MÜHENDİSLİK FAKÜLTESİ
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ
ELN2104 Elektrik Devreleri Laboratuarı II –2013-2014 Bahar
DENEY 1
İşlemsel Kuvvetlendiricili (OP-AMP)
Devrelerin AC Uygulamaları
Deneyi Yapanın
Adı – Soyadı
Numarası
Deney Grubu
Deney Tarihi
İmza
Değerlendirme
:
Ön Hazırlık ve Deney Bilgisi
(20 / 100)
:
/ 100
Deney Düzeneği Kurulumu
(15 / 100)
:
/ 100
Ölçü Aletlerinin Kullanımı
(20 / 100)
:
/ 100
Deney Sonuçları
(30 / 100)
:
/ 100
Zamanında Tamamlama
(15 / 100)
:
/ 100
DENEY NOTU
(100 / 100)
:
/ 100
Sonuçların Yorumlanması
(90 / 100)
:
/ 100
Rapor Düzeni
(10 / 100)
:
/ 100
RAPOR NOTU
(100 / 100)
:
/ 100
:
:
:
:
Değerlendiren :
Doç. Dr. Figen ERTAŞ
2013-2014 Bahar
Deney 1: İşlemsel Kuvvetlendiricili (OP-AMP) Devrelerin AC Uygulamaları
AMAÇLAR
1. Op-amplı devrelerde besleme gerilimi ve yük direncinin çıkış gerilimine etkisinin incelenmesi
2. Op-amplı devrelerin giriş ve çıkış işaretleri arasındaki kazanç ve faz farklarının ölçülmesi
3. İstenilen değerde kazanç ve faz farkına sahip op-amplı devre tasarımının yapılması
ÖNBİLGİ
1. Op-amp bacak (pin) bağlantıları
1
8
VCC
2
Vref
_
Vin
3
Ro
7
6
A
+
1
Vo
Vref
4
Vin
VEE
VEE
2
7
_
A
3
6
+
4
VCC
Vo
5
(a)
Vref
Vin
VEE
+
2
7
A.Vi
Ri
3
8
6
Vi
_
4
(b)
VCC
Vo
5
(c)
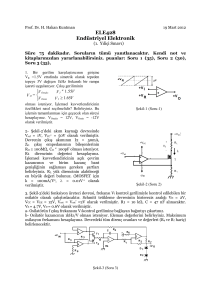
Şekil 1. LM741 tümdevresinin bacak bağlantıları
2. Çıkış gerilimi maksimum değerinin sınırlanması
Op-amplı bir devrenin girişine sinüzoidal bir işaret uygulandığında çıkış gerilimi de VEE<V0<VCC
şartını sağlayacak şekilde sinüzoidal bir işaret olur (Şekil 2a). Eğer giriş gerilimi tepe değeri (V2)’nin
kazançla çarpılmasıyla elde edilen çıkış gerilimi tepe değeri (K·V2) yukarıda belirtilen şartı
sağlamazsa, çıkış işaretinde kırpılma meydana gelir (Şekil 2b).
Vin
Vo
K.V1
V1
Vin
Vo
VCC
V2
Vo
K.V2
p-p
t
t
t
t
VEE
(a)
(b)
Şekil 2. Evirmeyen kuvvetlendiricide a) kırpılmasız b) kırpılmalı durumda giriş ve çıkış işaretlerinin
değişimi
Şekil 1c’deki op-amp eşdeğeri göz önüne alınırsa, op-amplı devrenin çıkışına bir yük direnci
bağlanarak op-amptan akım çekildiğinde, çıkış direnci (R0) üzerinde bir gerilim düşümü meydana
gelir. Bu durumda çıkış gerilimi maksimum değeri VEE+VRo<V0<VCC-VRo şartıyla sınırlanır. Bu
nedenle kırpılmasız durumda elde edilebilecek maksimum “tepeden tepeye çıkış gerilimi ( V0( p p ) )”
değeri küçülür. Vp-p (p-p: peak to peak, tepeden tepeye) değeri, işaretin maksimum ve minimum
değerleri arasındaki farktır.
Tarih ve İmza:
1
Doç. Dr. Figen ERTAŞ
2013-2014 Bahar
Şekil 3b’de evirmeyen bir kuvvetlendiriciye ait çıkış geriliminin, giriş gerilimi ile değişimini ifade
eden grafik görülmektedir. Bu grafik, osiloskobun XY modunda ölçüm yapılarak elde edilebilir.
R2
Vo <VCC
Vo
max
VCC
R1
_
Vin
Vo
Vin
+
+
VEE
Vo >VEE
min
(a)
(b)
Şekil 3. Evirmeyen kuvvetlendiricide çıkış işaretinin giriş işareti ile değişimi
XY modunda çalışan osiloskopta CH1 (kanal 1) girişine uygulanan işaret düşey (y) ekseni, CH2 (kanal
2) girişine uygulanan işaret ise yatay (x) ekseni tarar. Bu sayede çıkış işaretinin giriş işaretine göre
değişimi ekranda görüntülenir.
3. Op-amplı fazör devreler
Şekil 4’de op-amplı eviren ve evirmeyen kuvvetlendirici devreleri ve transfer fonksiyonları
görülmektedir. Devreler Z1 ve Z2 empedanslarını içermektedir. Burada Vin ve Vo ifadeleri, sinüzoidal
giriş ve çıkış gerilimlerinin fazör gösterimleridir.
Z2
Z2
VCC
VCC
Vin
_
Z1
_
Z1
Vo
+
Vo
Vin
Vo
Z
2
Vin
Z1
VEE
+
Vo
Z
1 2
Vin
Z1
VEE
(a)
(b)
Şekil 4. Op-amplı a) eviren b) evirmeyen kuvvetlendirici devreleri
4. Op-amplı türev alıcı devre
Şekil 4a’da görülen eviren kuvvetlendirici devresinde Z1 empedansı bir C kondansatöründen ve Z2
empedansı bir R direncinden oluştuğunda, devre bir türev alıcı olarak davranır (Şekil 5a).
R
R
VCC
C
Rs
_
Vin
Vin
C
VCC
_
Vo
Vo
+
+
VEE
VEE
(a)
(b)
Şekil 5. a) Basit bir türev alıcı devre b) seri direnç eklenmiş türev alıcı devre
Tarih ve İmza:
2
Doç. Dr. Figen ERTAŞ
2013-2014 Bahar
Basit bir türev alıcı devrede karşılaşılan en temel problem, artan frekansla kapasitif reaktansın
azalması ve bunun da devrenin kazancının artmasına neden olmasıdır. Reaktanstaki bu değişiklikten
dolayı devre yüksek frekans gürültülerine karşı çok hassastır. Bu durumda yüksek frekans kazancına
bir limit koymak için Şekil 5b’deki gibi kondansatöre seri bir direnç (Rs) eklenir. Rs direncinin
eklenmesi, kazanç ve faz farkının değişmesine neden olur.
5. Op-amplı integral alıcı devre
Şekil 4a’da görülen eviren kuvvetlendirici devresinde Z1 empedansı bir R direncinden ve Z2
empedansı bir C kondansatöründen oluştuğunda devre bir integral alıcı olarak davranır (Şekil 6a).
C
C
R
Vin
Rp
VCC
_
VCC
R
_
Vin
Vo
Vo
+
+
VEE
VEE
(a)
(b)
Şekil 6. a) Basit bir integral alıcı devre b) paralel direnç eklenmiş integral alıcı devre
Türev alıcıdakine benzer bir problem, integral alıcı devre için de geçerlidir. Kondansatörün reaktansı
azalan frekansla birlikte artar ve dolayısıyla DC kazancı aşırı derecede yüksek olur. DC kazancı
sınırlamak için Şekil 6b’de görüldüğü gibi, C kondansatörüne paralel olarak bir direnç (Rp)
yerleştirilir. Devre, DC’de (sıfır frekans) eviren kuvvetlendirici gibi davranır. R p direncinin eklenmesi,
kazanç ve faz farkının değişmesine neden olur.
6. İki işaret arasındaki faz farkının ölçümü
İki işaret arasındaki faz farkı, osiloskop kullanılarak iki farklı yöntemle ölçülebilir. Osiloskop normal
tarama modunda çalıştırılırken, her iki işaretin zamana bağlı değişimi ekranda gözlenir. İşaretlerin
sıfırdan geçiş anları arasındaki zaman farkı, işaretlerin periyotlarına oranlanarak faz farkı bulunur.
(Şekil 7a). Diğer yöntemde ise osiloskobun XY modunda ölçüm yapılır. Şekil 7b’de görülen eğri
yardımıyla sin = B/A formülünden faz farkı hesaplanır. Düşey ve yatay eksenlerin belirlenebilmesi
için kanallardan biri kapatılarak, tek bir kanalın ekranı taraması sağlanır.
y
V
B
t1
y
A
t
t
1
360 T
T
B
A
x
sin (180 -) B / A
sin B / A
(a)
x
(b)
Şekil 7. İki işaret arasındaki faz farkının a) normal tarama modunda b) XY modunda ölçümü
Tarih ve İmza:
3
Doç. Dr. Figen ERTAŞ
2013-2014 Bahar
ÖN HAZIRLIK
1. Şekil 4a ve 4b’deki devrelerde Z1 = R1 + jX1 ve Z2 = R2 + jX2 olarak alıp her bir devre için Vo/Vin
ifadelerini en sade biçimde (a+jb formunda) bulunuz.
Şekil 4a:
Vo
Vin
Şekil 4b:
Vo
Vin
2. Ön hazırlık 1'de bulduğunuz V0/Vin ifadelerini kullanarak Şekil 5a, 5b, 6a ve 6b’deki devrelere ait
V0/Vin ifadelerinin fazör gösterimlerini (genlik ve faz farkı biçiminde) bulunuz.
Ör: Şekil 5a: R1=0
X1= 1 wC
R2=R
X2=0
V0
R wC
j
jwRC wRC 90
Vin
1 w2C 2
Şekil 5b:
R1 =
X1=
R2 =
X2=
R1 =
X1=
R2 =
X2=
R1 =
X1=
R2 =
X2=
V0
Vin
Şekil 6a:
V0
Vin
Şekil 6b:
V0
Vin
3. Şekil 6b’deki devrenin girişine Vin (t ) sin(2 1000t ) işareti uygulandığında çıkış işaretinin
V0 (t ) 3,1 sin(2 1000t 121 ) olması için gerekli olan R ve Rp değerlerini ön hazırlık 2'de
bulduğunuz formüller yardımıyla hesaplayınız (C=22nF alınız).
4. Ön hazırlık 3'de incelediğiniz devrede Rp direnci kaldırıldığında elde edilecek V0(t) işaretini
bulunuz.
Tarih ve İmza:
4
Doç. Dr. Figen ERTAŞ
2013-2014 Bahar
Öneri: Deneyde kullanılacak devreleri laboratuvar öncesinde kurarak (Workbench veya laboratuvar
ortamında) çalıştırmanız, deney sırasında hızlı ve doğru sonuçlar elde etmenize yardımcı olabilir.
DENEYDE KULLANILACAKLAR
Çift kanallı osiloskop (osiloskobun tanıtım dokümanını fotokopiden alabilirsiniz),
Sinyal jeneratörü, BNC konnektör,
LM741 op-amp tümdevresi,
Kondansatör: 22nF,
Dirençler: 330, 2k 10k, 12k270k
DENEYİN YAPILIŞI
1. Op-amplı evirmeyen kuvvetlendiricide kırpılmasız maksimum çıkış geriliminin ölçümü
1.1. Şekil 8’deki op-amplı evirmeyen kuvvetlendirici devresini kurunuz.
Şekil 8. Op-amplı evirmeyen kuvvetlendirici devresi
1.2. Sinyal jeneratörünü kullanarak devrenin girişine (sinyal jeneratörünün 50 ’luk çıkışından
Board’un BNC girişine) 1kHz frekansında sinüzoidal işaret uygulayınız. Çift kanallı osiloskop
yardımıyla giriş ve çıkış (Vin ve V0) işaretlerini aynı anda gözleyiniz.
1.3. Giriş işaretinin genliğini, çıkış işaretinin negatif veya pozitif tepe değerinde kırpılmanın
oluşmaya başladığı değere ayarlayınız.
1.4. Çıkış işaretinde kırpılma olmadan (sinüzoidal formu bozulmadan) elde edilebilecek maksimum
“tepeden tepeye çıkış gerilimi ( V0( p p ) )” değerini osiloskoptan okuyunuz. VCC ve VEE değerlerini
de voltmetre yardımıyla ölçerek Tablo 1’e kaydediniz (yük direnci yok).
VCC
VEE
Tablo 1. Maksimum çıkış gerilimi ölçümü
VCC - VEE
V0( p p ) (max), yük direnci yok V0( p p ) (max), Ry = 330
1.5. Devrenin çıkışına (V0 ile toprak arasına) bir Ry = 330 yük direnci bağlayıp, ölçümleri
tekrarlayarak, bulduğunuz V0( p p ) (max) değerlerini Tablo 1’e kaydediniz.
Yorum 1: Yük direnci yok iken V0( p p ) (max) neden VCC-VEE’den küçük çıkmıştır?
Yorum 2: Yük direncinin eklenmesi V0( p p ) (max)’ı neden düşürmüştür?
Tarih ve İmza:
5
Doç. Dr. Figen ERTAŞ
2013-2014 Bahar
2. Op-amplı evirmeyen kuvvetlendiricide gerilim kazancı ölçümü ve giriş-çıkış grafiğinin elde
edilmesi
2.1. Şekil 8’deki devrede (yük direnci yok iken) girişe Vin( p p ) 0.4V ve f=1kHz değerinde sinüzoidal
işaret uygulayınız. Çıkış işaretinin genliğini ölçerek devrenin kazancını hesaplayınız ve elde
ettiğiniz değerleri Tablo 2’ye kaydediniz.
V0( p p )
Tablo 2. Gerilim kazancı ölçümleri
R
V
(ölçülen) V0( p p ) (ölçülen) Av 0 (ölçülen) A v 1 2 (hesaplanan)
R1
Vin
0.4V
28
Yorum 3: Kullandığınız dirençlerin toleranslarını göz önünde bulundurarak en büyük ve en küçük
kazanç değerinin ne olarak ölçülebileceğini hesaplayınız. Ölçtüğünüz değer bu aralıkta mı?
2.2. Osiloskobu XY modunda çalıştırarak giriş ve çıkış işaretlerinin birbirlerine bağlı değişimini
ifade eden grafiği elde ediniz. Düşey eksenin çıkış, yatay eksenin ise giriş işareti ile taranıyor
olmasına dikkat ediniz. Giriş işaretinin genliğini değiştirerek kırpılma öncesi ve sonrası durum
için elde edilen grafikleri Şekil 9’da gösteriniz.
CH1=
V/div
CH2=
a) Kırpılmasız durum
CH1=
V/div
V/div
CH2=
V/div
b) Kırpılmalı durum
Şekil 9. XY modu dalga şekilleri
Yorum 4: Şekil 9’da elde ettiğiniz grafikleri yorumlayınız. Bu grafiklerden hangi bilgiler elde
edilebilir?
Tarih ve İmza:
6
Doç. Dr. Figen ERTAŞ
2013-2014 Bahar
3. Op-amplı eviren kuvvetlendiricide gerilim kazancı ölçümü ve giriş-çıkış grafiğinin elde
edilmesi
Şekil 10. Op-amplı eviren kuvvetlendirici devresi
3.1. Şekil 10’daki devrede girişe Vin( p p ) 0.4V ve f=1kHz değerinde işaret uygulayınız. Çıkış
işaretinin genliğini ölçerek devrenin kazancını hesaplayınız ve elde ettiğiniz değerleri
Tablo 3’e kaydediniz.
Vin ( p p ) (ölçülen)
Tablo 3. Gerilim kazancı ölçümleri
R
V
A v 2 (hesaplanan)
V0( p p ) (ölçülen)
Av 0 (ölçülen)
R1
Vin
0.4V
-27
3.2. Osiloskobu XY modunda çalıştırarak giriş ve çıkış işaretlerinin birbirlerine bağlı değişimini
ifade eden grafiği elde ediniz. Düşey eksenin çıkış, yatay eksenin ise giriş işareti ile taranıyor
olmasına dikkat ediniz. Giriş işaretinin genliğini değiştirerek kırpılma öncesi ve sonrası
durum için elde edilen grafikleri Şekil 11’de gösteriniz.
CH1=
V/div
CH2=
V/div
CH1=
V/div
CH2=
V/div
a) Kırpılmasız durum
b) Kırpılmalı durum
Şekil 11. XY modu dalga şekilleri
Yorum 5: Şekil 11'de elde ettiğiniz grafikleri yorumlayınız.
Tarih ve İmza:
ERTAŞ
7
Doç. Dr. Figen
2013-2014 Bahar
4. Op-amplı integral alıcı devresinin giriş ve çıkış işaretleri arasındaki ilişkinin (kazanç ve faz
farkının) incelenmesi
4.1. Ön hazırlık 3'te bulduğunuz R=2k, Rp=12k ve C=22nF değerlerini kullanarak
Şekil 12'deki devreyi kurunuz.
C
Rp
R
Vin
VCC
_
Vo
+
VEE
Şekil 12. Paralel direnç eklenmiş integral alıcı devre
4.2. Devrenin girişine Vin( p p ) 1V ve f=1kHz değerinde sinüzoidal işaret uygulayınız.
4.3. Rp'nin devrede bulunduğu ve bulunmadığı durumlara ait kazanç ve faz farkı değerlerini bulup
Tablo 5'e kaydediniz.
Vin p p
Tablo 5. İntegral alıcı devre için kazanç ve faz farkı ölçümleri
V0
Faz eğrisinden ölçülen
V0 p p Av p p
Av
B
180 sin 1
Vin p p
(ön hazırlık)
A
A değeri
B değeri
(ön hazırlık)
(ölçülen)
Rp
var
Rp
yok
1V
3,1
121º
1V
3,6
90º
Yorum 6: Rp direncinin bulunduğu ve bulunmadığı durumlar için, hangi devrenin gerçek integral
alıcı devre olduğunu nedeni ile belirtiniz.
Yorum 7: Yaptığınız deneylerde, ölçümlerle teorik sonuçlar arasında oluşan farka aşağıda
verilenlerden hangileri neden olabilir? Her birinin önemini belirtiniz.
Kullanılan elemanların (direnç ve kondansatörün) toleransları
Op-amp çıkış direncinin çıkış gerilimini sınırlaması
Besleme geriliminin tam olarak verilememesi
Kullanılan bağlantı tellerinin dirençleri
Op-ampın girişinden akım çekmesi
Tarih ve İmza:
ERTAŞ
8
Doç. Dr. Figen