AC (ALTERNATİF AKIM)
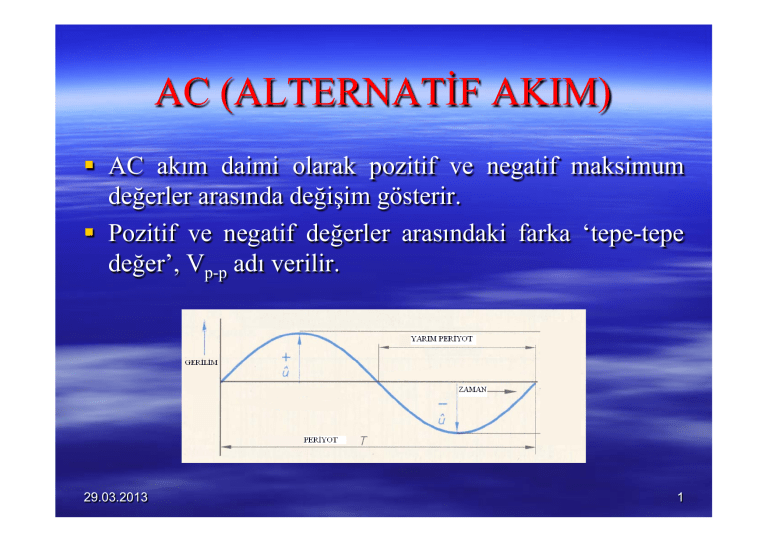
§ AC akım daimi olarak pozitif ve negatif maksimum
değerler arasında değişim gösterir.
§ Pozitif ve negatif değerler arasındaki farka ‘tepe-tepe
değer’, Vp-p adı verilir.
29.03.2013
1
AC (ALTERNATİF AKIM)
§ Sinyalin bir periyot süresinde ulaştığı maksimum
değere ‘Amplitud’ adı verilir.
§ Sinyalin başlangıç değerine ulaşması için geçen süreye
ise ‘periyot’ (tam devir) adı verilir.
29.03.2013
2
AC (ALTERNATİF AKIM)
§ AC devrelerde sinüzoidal gerilim üretilir.
∧
u = u* sin α
u: anlık değer
û: maksimum değer
sin α: dönüş açısının sinüs değeri
w = 2* π*f w: dairesel frekans 2*π =
360°
29.03.2013
3
AC AKIMIN ORTALAMADEĞERİ
§ Alternatif akımda ortalama değer bir periyottaki ani
değerlerin ortalamasıdır.
U or
u1 + u 2 + u 3 + ...u n
=
n
Uor : gerilimin ortalama değeri (volt)
Un : gerilimin ani değeri (volt)
N : ani değer sayısı
AC akımda pozitif ani değer sayısı negatif ani değer
sayısına eşittir!
Ortalama değer sıfıra eşittir.
29.03.2013
4
AC AKIMIN ORTALAMA DEĞERİ
§ Hesaplarda ani değer sayısının
fazla olması sonucun gerçek
değere daha yakın olmasını
sağlar.
§ Bir periyodunun ortalama
değeri sıfır olan akımlara
alternatif akım (AC) denir.
§ Ortalama değerin hesaplanması
için yarım periyot kullanılır.
I or
0.1736 + 0.5 + 0.766 + 0.9397 + 1 + 0.9397 + 0.766 + 0.5 + 0.1736
=
9
I or = 0.6398 * I m
29.03.2013
5
AC AKIMIN ORTALAMA DEĞERİ
T /2
U or
U or
U or
U or
29.03.2013
1
=
U m * sin wt
∫
T /2 0
2
1
T /2
= U m * − cos wt 0
T
w
2 T
2π T
= Um *
* −(cos
* − cos 0)
T 2π
T 2
2
= Um
π
6
AC AKIMIN ETKİN (EFEKTİF)
DEĞERİ
§ Etkin değer doğru akımın (DC) yaptığı işe eşit iş yapan
AC’nin doğru akıma eş olan değeridir.
V
W
=
t
§ Doğru akımın yaptığı iş:
R
§ Alternatif akımın yaptığı iş ani değerlerin karesi ile
orantılıdır.
2
2
2
2
2
U ef
u1 + u 2 + u 3 + ....u n
=
n
Uef : gerilimin etkin değeri (volt)
un : gerilimin ani değeri (volt)
n : ani değer sayısı
29.03.2013
7
AC AKIMIN ETKİN (EFEKTİF)
DEĞERİ
§ Etkin değer hesabında
ani değerlerin karelerinin
toplamı alındığı için
negatif ani değerlerin
toplamı da pozitif olur.
I ef
0.1736 2 + 0.5 2 + 0.766 2 + 0.9397 2 + 12 + 0.9397 2 + 0.766 2 + 0.5 2 + 0.1736 2
=
9
I ef = 0.7072 * I m
29.03.2013
8
AC AKIMIN ETKİN (EFEKTİF)
DEĞERİ
T
U ef
1
=
* ∫ (U m sin wt ) 2
T 0
T
U ef = U m
1 1 − cos 2 wt
*∫
T 0
2
U ef = U m
1 t sin 2 wt T
( −
)0
T 2
4w
U ef = U m
1 T
*
T 2
U ef =
29.03.2013
1 − cos 2α
sin α =
2
2
Um
2
9
AC AKIMDA DEVRE ELEMANLARI
§ ETKİN DİRENÇ:
§ Bir direnç, AC gerilim altında DC
gerilimdeki özelliklere sahipse etkin
direnç olarak adlandırılır. (ısıtıcı
ocaklar, akkor telli ampul,..)
Etkin direnç kullanıldığında akım ve gerilim aynı faz
açısına sahiptir. Direnç üzerinde elektrik enerjisi ısı
29.03.2013
10
enerjisine dönüşür.
AC AKIMDA DEVRE ELEMANLARI
§ ENDÜKTİF REAKTANS
§ Endüktif reaktans bobinin üzerinde oluşan
endüktans sonucu meydana gelir. (ters yönde
gerilim oluşur!)
§ Bobinin endüktif reaktansı, gerilimin
frekansına ve bobinin endüktansına bağlı
olarak değişir.
§ Endüktif
devrede akım
gerilimi 90°
geriden takip
eder.
29.03.2013
11
AC AKIMDA DEVRE ELEMANLARI
u = U m sin wt
di
dt
e L = −u
eL − L
di
dt
di U m sin wt
=
dt
L
−Um
i=
cos wt
Lw
U
π
i = m sin( wt − )
Lw
2
U m = I m * Lw
− cos wt = sin( wt −
π
2
)
u=L
XL : endüktif reaktans (Ω)
w : dairesel frekans
L: endüktans (H)
X L = wL
29.03.2013
12
AC AKIMDA DEVRE ELEMANLARI
§ KAPASİTİF REAKTANS
§ Gerilim akımı 90° geriden takip eder.
§ Kapasitenin reaktansı, uygulanan
gerilimin frekansına ve kapasiteye bağlı
olarak ters yönde değişim gösterir.
29.03.2013
13
AC AKIMDA DEVRE ELEMANLARI
u = U m sin wt
du
i=C
dt
i = CwU m sin( wt +
CwU m = I m
i = I m sin( wt +
π
2
)
π
2
)
Xc : kapasitif reaktans (Ω)
w : dairesel frekans
C: kapasite (F)
1
Im
wC
1
Xc =
wC
Um =
29.03.2013
14
ETKİN DİRENÇ, KAPASİTİF VE
ENDÜKTİF REAKTANSIN SERİ
BAĞLANMASI
§ Seri bağlantılarda kapasitif ve
endüktif reaktanslar zıt yönde etki
ederler. (kapasitede akım 90° önde,
bobinde ise 90° geridedir.
§ Vektörel gösterimde toplam
gerilim, gerilimlerin geometrik
toplamına eşittir.
U: toplam gerilim
Uw: etkin gerilim
U bL : reaktif gerilim (endüktif)
U bC : reaktif gerilim (kapasitif)
29.03.2013
15
ETKİN DİRENÇ, KAPASİTİF VE
ENDÜKTİF REAKTANSIN SERİ
BAĞLANMASI
2
2
U = U w + (U bL − U bC ) 2
Z 2 = R 2 + ( X L − X C )2
Z = R2 + ( X L − X C )2
Z=
29.03.2013
U
I
U = U 2 w + (U bL − U bC ) 2
Z: empedans (Ω)
R: etkin direnç
XL : endüktif reaktans
XC : kapasitif reaktans
I: toplam akım (A)
U: toplam gerilim (V)
16
ETKİN DİRENÇ, KAPASİTİF VE
ENDÜKTİF REAKTANSIN PARALEL
BAĞLANMASI
§ Paralel bağlantılarda, bobinden
geçen akım gerilimin
90°
gerisinde, kapasiteden geçen
akım ise 90° ilerisindedir.
§ Kapasitif ve endüktif reaktif
akım aynı doğru üzerinde ancak
zıt yönlerdedir. Toplam akım,
etkin ve reaktif akımların
geometrik toplamına eşittir.
29.03.2013
17
ETKİN DİRENÇ, KAPASİTİF VE
ENDÜKTİF REAKTANSIN PARALEL
BAĞLANMASI
2
I 2 = I w + ( I bC − I bL ) 2
I = I 2 w + ( I bC − I bL ) 2
Y 2 = G 2 + ( BC − BL ) 2
Y = G 2 + ( BC − BL ) 2
29.03.2013
I : toplam akım
Iw : etkin akım
IbL : reaktif akım (endüktif)
IbC : reaktif akım (kapasitif)
Y : toplam iletkenlik
G : etkin iletkenlik
BC : kapasitif iletkenlik
BL : endüktif iletkenlik
18
