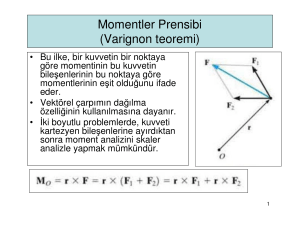
Momentler Prensibi (Varignon teoremi)

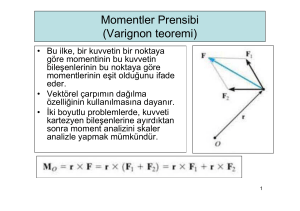
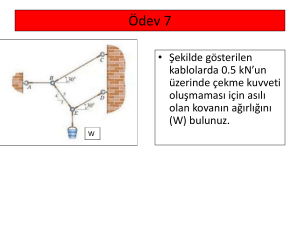
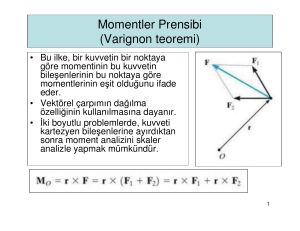
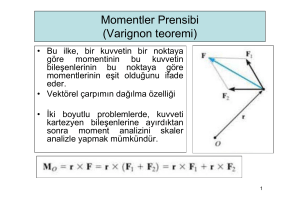
Momentler Prensibi
(Varignon teoremi)
• Bu ilke, bir kuvvetin bir noktaya
göre momentinin bu kuvvetin
bileşenlerinin bu noktaya göre
momentlerinin eşit olduğunu ifade
eder.
• Vektörel çarpımın dağılma
özelliğinin kullanılmasına dayanır.
• İki boyutlu problemlerde, kuvveti
kartezyen bileşenlerine ayırdıktan
sonra moment analizini skaler
analizle yapmak mümkündür.
1
Momentler Prensibi
(Varignon teoremi)
F kuvvetine dik mesafeyi (d)
bulmaya gerek kalmadan,
bileşenlerine ayırmak daha
pratik !
2
Örnek 25
• O noktasında oluşan
momenti belirleyiniz.
ÇÖZÜM 1
3
ÇÖZÜM 2
4
ÇÖZÜM 3
5
Örnek 26
F kuvveti şekildeki desteğin
köşesinde etki etmektedir. Kuvvetin
O noktasına göre momentini
belirleyiniz (skaler ve vektörel
çözüm ile).
Çözüm 1- skaler analiz
6
Çözüm 2- vektörel analiz
7
Örnek 27
6m
• Sokak lambasını
kaldırmak için F
kuvvetinin A
noktasında 2250 Nm
saatin tersi yönünde
moment oluşturması
gerekmektedir. Bu
durumda F kuvvetinin
şiddeti ne olmalıdır?
3m
8
1.yol: A noktasına dik mesafeyi (d) bulalım.
5.802  4.552  7.37m

F
3m
75°
6xcos75=1.55m
  23.15

6m
.
d
105°
sin 105 sin 

7.37
3.0
sin   (3 sin 105) / 7.37
6xsin75=5.80m
A
d  6  sin 23.15  2.36 m
M A  Fd ( skaler)
2250  F  2.36  F  953.39 N
6m
3m
9
2.yol: F kuvveti bileşenlerine ayrılır. B noktasına etkiyen F kuvveti
bileşenlerinin A’da yaratmış oldukları moment toplamını 2250 Nm yapan
kuvvet bulunur.
Fx
6m
 105°
3m
=23.15°
B

 Fy
=51.85°
5.80m
Fx=F.cos 51.85
A
1.55m
Fy=F.sin 51.85
MA=2250 = Fx(5.80) – Fy(1.55)
2250 = F cos (5.80) – F sin (1.55)
F=953.39 N
10
Bir kuvvetin bir eksene göre momenti
• Bir kuvvetin bir noktaya göre momenti hesaplanırken,
moment ve moment ekseninin, kuvvet ve moment kolunu
içeren düzleme daima dik olduğu unutulmamalıdır. Bazen
bu momentin, söz konusu noktadan geçen belirli bir eksen
üzerindeki bileşenini bulmak gerekebilir. Skaler veya
vektörel analiz kullanılabilir.
Örn:
Bulonu gevşetebilecek
moment y ekseni
etrafındaki My momentidir.
x ekseni etrafında oluşan
momentin bulonu
gevşetmeye bir etkisi
yoktur.
11
Skaler hesap
• F kuvvetinin y ekseni etrafında moment yaratan
moment kolu: “dy=dcos” olduğuna göre,
M= Fdy = F(dcos)
olarak bulunur.
12
Vektörel hesap
• Şekilde gösterilen F
kuvvetinin y eksenine
göre momentini bulmak
için önce, F kuvvetinin y
ekseni üzerinde herhangi
bir nokta “O”ya göre
momenti bulunur.
Mo momentinin y eksenine göre izdüşümü olan My bileşeni (y ekseni
etrafındaki moment) ise skaler çarpım kullanılarak bulunur.
(sonuç skaler)
y eksenindeki birim vektör
13
HATıRLATMA !- SKALER ÇARPıM –
BÖLÜM2’DEN
Bir vektörün bir doğruya paralel ve dik bileşenlerinin
bulunması:
Aa: a-a doğrultusundaki A vektörünün bileşeni. A’nın izdüşümü de denir.
a-a’nın doğrultusu ua birim vektörüyle belirlenmişse, Aa vektörünün şiddeti
skaler çarpımla bulunabilir.
 
Aa  A  ua
(ua  1)
 Au a cos   A cos 
 
Aa  A  ua şeklinde bulunur .
14
Genelleştirince:
  
M a  ua ( r  F )
Bu çarpıma skaler üçlü çarpım denir.
Vektörler kartezyen formda ifade edilirse;
Skaler üçlü çarpım determinant formda da yazılabilir:
15
1. Satır
2. Satır
3. Satır
1.satır: a-a' ekseninin yönünü belirleyen birim vektörün kartezyen bileşenleri
2.satır: a-a ekseninin herhangi bir yerinden, F kuvvetinin etki çizgisinin
herhangi bir yerine olan pozisyon vektörünün kartezyen bileşenleri
3. satır: F kuvvetinin kartezyen bileşenleri
Ma belirlendiğinde Ma’yı kartezyen vektör şeklinde ifade edebiliriz :
Ma negatif çıkarsa


M a  M a ua
 
M a u a ‘nın tersi yönündedir.
16
Örnek 28
•
F kuvvetinin OA borusunun
doğrultusundan geçen eksene göre
oluşan momentin şiddetini bulunuz.
Kartezyen vektör cinsinden ifade
ediniz.
17
Örnek 29
Şekildeki dikdörtgen levha A ve B dirsekleri ve CD kablosu ile yz-düzlemindeki bir
duvara bağlanmıştır. CD kablosunun taşıdığı kuvvet 200 N’dur. D’nin koordinatları:
.
D(0, 360, 120)
mm’dir. Buna göre tel tarafından C noktasına uygulanan bu kuvvetin;
a)A noktasına göre momentini
b)AE eksenine göre momentini bulunuz
Çözümü sınıfta yapılacaktır.
Kuvvet Çiftleri
• Kuvvet çifti, aralarındaki dik uzaklık d olan,
aynı büyüklükte ve zıt yöndeki paralel iki
kuvvet olarak tanımlanır.
• Bileşke kuvvet sıfır olduğundan, kuvvet
çiftinin tek etkisi dönme eğilimi yaratmaktır.
Kuvvet çifti ile üretilen moment, bir
O noktasında oluşan iki kuvvetin
momentleri toplamına eşittir.
   


 
M  rB  F  rA  ( F )  (rB  rA )  F
     
rB  rA  r r  rB  rA
  
M  r F
Momentin, rA, rB konum vektörlerine
değil, sadece kuvvetler arasındaki
konum vektörüne bağlı olması
nedeniyle, kuvvet çiftinin momentinin
bir serbest vektör olduğu, herhangi 21
bir
noktada etki edebileceği söylenebilir.
Skaler Formülasyon
Kuvvet çiftinin momenti:
M  Fd
F= kuvvetlerden birinin büyüklüğü
d= kuvvetler arasındaki dik uzaklık (moment kolu)
Kuvvet çifti momentinin doğrultu ve yönü sağ el
kuralı ile belirlenir.
Vektörel Formülasyon
Kuvvet çiftinin momenti vektörel
(çapraz) çarpımla:
  
M  r F
22
Eşdeğer (Denk) Kuvvet Çiftleri
• İki farklı kuvvet çifti, aynı şiddet ve yöne sahip moment etkisi
yaratıyorsa, bu iki kuvvet çiftine “eşdeğer kuvvet çifti” denir.
M= 30 N (0.4 m) = 40 N (0.3 m) = 12 Nm
23
Bileşke Moment
• Kuvvet çifti momentleri, serbest
vektörler olduğundan vektörel
olarak toplanabilirler.



M  M1  M 2

 
MR  r  F
• Cismin üzerine ikiden fazla
kuvvet çifti momenti etki ediyorsa
bu kavram genelleştirilebilir.
24
Örnek 30
• Üç farklı kuvvet çiftinin
cisim üzerinde yarattığı
bileşke momenti skaler
hesapla bulunuz.
MR  M
 M R   F1d1  F2 d 2  F3d 3
 (200 N )(0.4 m)  (450 N )(0.3 m)  (300 N )(0.5 m)
 95 Nm  95 Nm
25
Örnek 31
Boruya etkiyen iki kuvvet çiftinin yaratmış
olduğu momentin bileşkesini bulunuz.
26
Örnek 32
Boruya etkiyen kuvvet çiftinin
momentini belirleyiniz.
27
Vektörel çözüm
25 N
25 N
25 N
25 N
Skaler çözüm
Kuvvet ve Kuvvet Çifti Sistemlerinin Basitleştirilmesi
•
Bazen bir kuvvet ve moment sistemini daha basit ve eşdeğer başka bir
kuvvet sistemine indirgemek gerekebilir. Bu eşdeğer sistem belli bir noktaya
etkiyen bileşke kuvvet ve momentten oluşmalıdır. Bu yeni sistem, orijinal
sistemle aynı dış etkileri yaratıyorsa, yeni kuvvet sistemine “eşdeğer kuvvet
sistemi” denir.
•
Dış etkiler,
– Eğer cisim herhangi bir yere bağlı değilse ötelenme ve dönme etkileridir
– Eğer cisim mesnetli ise (bağlı) yarattığı mesnet tepkileridir
30
Kuvvet ve kuvvet çifti sisteminin bileşkesi
•
Bir rijit cisme kuvvetler ve kuvvet çifti momentlerinden
oluşan bir sistem etkiyorsa, cisim üzerindeki dış etkileri,
kuvvet ve kuvvet çifti momenti bileşkelerini kullanarak
incelemek daha basittir.
•
M kuvvet çifti momenti, bir serbest vektör olduğundan,
doğrudan O noktasına taşınır.
F1 ve F2 kayan vektörlerdir ve O noktası bu kuvvetlerin etki
çizgisi üzerinde olmadığından moment oluşturur. Oluşan
momentler de O noktasına taşınmalıdır.
•

 
M 1  r1  F1

 
FR  F1  F2

 
M 2  r2  F2

 

M R  M  M1  M 2


 FR  Fi 

M RO   M O   M
31
• Eğer kuvvet sistemi x-y
düzleminde ise, ve momentler de
bu düzleme dik (z ekseni
doğrultusunda) ise, yukarıdaki
vektör formülasyon, skaler
formülasyon halini alır.
FRx   Fx
FRy   Fy
M RO   M O ,i   M j
32
Örnek 33
Etkiyen kuvvetleri O noktasında eşdeğer
kuvvet ve moment sistemine indirgeyin.
Kuvvet Toplamı
33
Moment Toplamı
34
Örnek 34
Soru: Etkiyen kuvvetleri ve momenti O
noktasında eşdeğer bileşke kuvvet ve
moment sistemine indirgeyin.
Problem 3 boyutlu olduğu için vektörel
analizle daha kolay çözülebilir, bunun
yanısıra skaler çözüm de yapmak
mümkündür.
35
VEKTÖREL ANALİZ
Kuvvet Toplamı
36
Moment Toplamı
37
Kuvvet Sistemlerinin Daha da Basitleştirilmesi
• Bir kuvvet sistemi, aynı noktaya etkir veya aynı
düzlemde bulunur ya da paralelse, tek bir P noktasında
etkiyen bir tek bileşke kuvvete indirgenebilir. Çünkü bu
hallerin herbirinde FR ve MRO kuvvet sistemi, herhangi bir
O noktasında basitleştirildiğinde daima birbirine dik olur.
38
Bir noktadan geçen kuvvet sistemleri
• Bütün kuvvetlerin etki çizgileri O noktasından geçiyorsa, kuvvet
sistemi moment oluşturmaz. Eşdeğer kuvvet sistemi kuvvetlerin
vektörel toplamıyla bulunur:


FR   Fi
39
Düzlemsel Kuvvet Sistemleri
Kuvvetlerin bulunduğu düzleme dik doğrutulu kuvvet çifti momentleri içerebilen
düzlemsel kuvvet sistemleri tek bir bileşke kuvvete indirgenebilir.
Kuvvetlerin bileşkesi :


FR   F olarak hesaplanır ve yine aynı düzlemdedir.
Kuvvetlerin oluşturduğu moment ekseni bu düzleme diktir. Dolayısıyla kuvvetlerin
bileşkesi FR O noktasına göre aynı momenti yaratacak şekilde, O’dan d kadar
mesafede konumlandırılabilir.


 
M RO   M   r  F
40
Paralel kuvvet sistemleri
• Bu sistem z eksenine paralel kuvvetlerden oluşmaktadır.
Bu durumda, O noktasındaki bileşke kuvvet de z
eksenine paralel olmak zorundadır.


FR   Fi
41
• Her bir kuvvet x-y düzlemindeki bir O noktasına taşındığında, bileşke
kuvvet sadece x ve y eksenlerine göre bileşenlere sahip olan bir kuvvet
çifti momenti üretir. Buna göre, oluşan bileşke momenti, FR bileşke
kuvvetine diktir. Bu nedenle kuvvet sistemi daha da basitleştirilerek tek
bir FR kuvvetine indirgenebilir. “d” mesafesi şu şekilde bulunur:
42
WR  W1  W2
W1d1  W2 d 2
d
WR
43
Örnek 35
• Kirişe etkiyen
kuvvet ve moment
sistemini eşdeğer
tek bir kuvvete
indirgeyiniz ve kirişi
kestiği yeri
bulunuz.
44
Kuvvet Toplamı
45
Moment Toplamı
46
Örnek 36
Şekildeki vince etkiyen kuvvetleri
eşdeğer tek bir kuvvete
indirgeyin ve bu kuvvetin etki
çizgisinin AB kolonunu ve BC
kirişini kestiği yerleri belirleyiniz.
175 N
Kuvvet Toplamı
260
47
Moment Toplamı
=
=
175 N
48
Veya;
=
x0
 y  2.29 m
y  11m  x  10.9 m
175 N
49
Örnek 37
Şekilde gösterilen döşeme
birbirine paralel dört kuvvetin
etkisi altındadır. Eşdeğer tekil
kuvvetin yönünü ve yerini
bulunuz.
50
KUVVET TOPLAMI
MOMENT TOPLAMI
Örnek 38
Şekilde gösterilen kuvvetlere ait eşdeğer kuvvetin O noktasından
geçmesi için gerekli FA ve FB kuvvetlerinin şiddetlerini bulunuz.
53
 Mx  0
R  0  FB  0.75  6  0.65  FA  0.6  8  0.70  0
0.75 FB  0.60 FA  1.7 kNm
1
 My  0
R  0  FA  0.15  6  0.10  FB  0.15  8  0.10  0
FB  FA  1.333kNm
0.75 FB  0.60 FA  1.7kNm
FB  FA  1.333kNm
2
0.75FB  0.6 FA  1.7
 0.75FB  0.75FA  1
FA  18kN
FB  16.67kN
Örnek 39
300 N
200 N
15 cm
60°
y
10 cm
O
x
15 cm
400 N
100 N
10 cm
80 Nm
10 cm
20 cm
25 cm
Şekilde verilen kuvvetler sistemini tek bir kuvvete indirgeyip bu kuvvetin
doğrultusunun x eksenini kestiği noktanın koordinatını hesaplayınız.
300 N
200 N
15 cm
60°
y
10 cm
O
x
15 cm
400 N
100 N
10 cm
80 Nm
10 cm
20 cm
25 cm
Mo  80  400  0,3  200  cos 60  0,1  300  0,25  200  sin 60  0,3  100  0,15
Mo  68.04 Nm

Rx    Fx  300  100  200. cos 60  100 N 
Ry     Fy  400  200. sin 60  226.79 N 
R  100 2  226.79 2  247.8 N
x
Mo 68.4

 0,3m  30cm
Ry 226.8
Ry=226.8 N
Rx=100N

R=247.8N
tan  
226.79
   66.2
100