YER MAĞNETİK ALANI ve
Manyetik Ölçü Aletleri
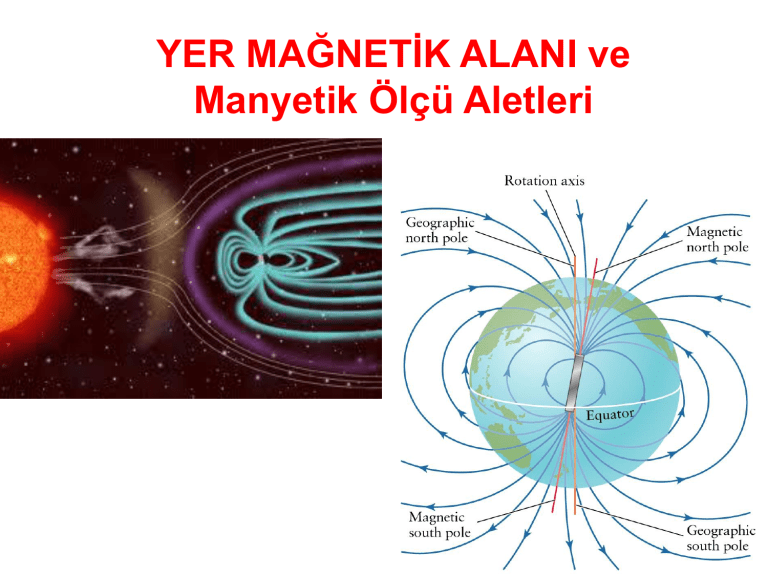
Gezegenimiz bir MANYETİK ALAN tarafından sarılmaktadır.
Bunun kanıtı pusula iğnesinin ibresinin
manyetik kuzeyinin kuzey kutbunu göstermesidir.
Dünya üzerinde bir noktada yer manyetik alanının ölçülmesi sonucunda elde edilen
değerler farklı kökenlere dayanan bileşenler içermektedir.
1. Jeodinamo mekanizması ile çalıştığı
düşünülen yerin dış sıvı çekirdeğinden
oluşan yer manyetik alanı
2. Yer kabuğunda mıknatıslanan kayaçlar
tarafından oluşan “KABUKSAL ALAN”.
3.İyonosferde akan elektrik akımları ve manyetosfer
tarafından meydana gelen dış manyetik alan
4. Elektromanyetik indüksiyon sonucu meydana
gelen manyetik alan. Bu alan kabuk ve üst mantoda
indüklenen elektrik alanlarından oluşmaktadır.
Sebebi; dış manyetik alanın zamana bağlı
değişimleridir.
MANYETİK ALAN
Uzayın herhangi bir noktasında bir
mıknatıs veya içinden akım geçen tele
etkiyen kuvvet alandır.
Manyetik alan
Elektrik akımdan kaynaklanabilir. Bunun
için I akımı geçene bir telin etrafında bir
manyetik alanın meydana gelmektedir.
Bir çubuk mıknatısta mıknatısı oluşturan
maddenin atom çekirdeklerinin etrafında
dönen elektronların meydana getirdikleri
elektrik akımından doğar.
MANYETİK ALAN VEKTÖREL BİR BÜYÜKLÜKTÜR.
Herhangi bir noktada manyetik alan bir doğrultu ve büyüklüğe sahiptir.
Oersted : bir telden geçen akım bir
manyetik alan oluşturur. Böylece
manyetik pusula telden geçen akıma
bağlı olarak yönelir. Akım içeri doğru ise
manyetik alan sağ yönlü, akım dışarı
doğru ise manyetik alan sol yönlüdür.
Eğer bir telden geçen akım bir mıknatıs üzerinde kuvvet
uygulayabiliyorsa, tersi durumda bir mıknatıs da bir tel üzerinde bir
kuvvet uygulayabilir.
Hareket etmeyen K-G yönlü bir mıknatıs göz önüne alalım. Bu mıknatıs
içerisinden K-G’e doğru bir manyetik alan meydana gelmektedir. K-G
kutuplar arasında bir iletken tel koyup içerisinden akım geçirelim.
Buna göre K-G mıknatıstan dolayı tel yukarı doğru bir kuvvete maruz kalır ( =
=iletken
tel üzerindeki kuvvet herzaman manyetik alan ile akımın vektörel çarpım yönündedir).
Elektrik alan kuvveti için
Fakat manyetik alan için herzaman çift
kutup olduğu için benzer eşitlik manyetik
alan kuvveti için yazılamaz.
Bir elektrik yükü olan ’’q’’ bir ’’v’’ hızıyla hareket ediyorsa
ayrıca
ve
q bağlıdır.
Lorentz kuvveti olarak ifade edilir.
Manyetik alan kuvvetinin birimi
NxCxm=1 Tesla (SI)
1 Gauss=10-4Tesla (Yer manyetik alanı
0.5 Gauss).
Oersted; Durağan akım durağan bir
manyetik alan meydana getirir.
Faraday; Durağan manyetik alan durağan
akım meydana getirir.
1. selenoide 2. Bir loop konuldu, 1.den
akım geçince 2. selenoid’de akım
geçmiyor. Durağan manyetik alan 2.
selenoid’deki bir akım meydana
getirmemiştir.
Değişen manyetik alan elektrik akımı meydana getirmektedir.
İletken teli bir mıknatısla birleştirelim. Eğer teli
hareket eden mıknatıs ile yakınlaştırırsak teldeki
akım mıknatısın meydana getirdiği alanı azaltacak
şekilde bir alan meydana getirir. Bu ’’LENZ
KANUNU’’ olarak bilinir
Telin içerisine bir mıknatıs koyup çıkardığımızda
ampermetrede
ne
kadar
akım
geçtiğini
görebilmekteyiz. Akım sadece mıknatısı hızlı bir
şekilde sokup çıkardığımızda olur. Indüklem akım
hareket eden bir kuvvetin sonucunda oluşur.
Eind.=Iind.R OHM KANUNU
Klasik Ölçü Aletleri
Sapma Açısı Ölçeri: Düşey bir eksen etrafında yermanyetik alan dışında
herhangi başka bir etki olmaksızın dönebilen ve manyetik momenti yatay
düzlemde olan bir mıknatısdan oluşmaktadır.
Jeologların kullandıkları pusula bir tür sapma açısı ölçerdir.
Sapma açısı ölçerde kullanılan mıknatısın şekli pusulada olduğu gibi iki ucu sivri
mekik biçiminde ya da askılı türde olduğu gibi silindir veya prizma şeklindedir.
Düşey eksen OO’, mıknatısın KG manyetik ekseni manyetik
Alanın yatay bileşeni ile çakışık olacak şekildedir. Manyetik
Alanın yatay bileşeni herhangi bir nedenle döndüğünde
mıknatıs Çubuk ve manyetik momenti de yatay bileşeni
izleyecektir.
Bu alette manyetik momentin yerinin belirlenmesi önemlidir.
askılı sapma açısı ölçerlerde mıknatısın KG uçlarına düzlem
ayna Yapıştırılır ve nokta izleme yöntemi ile mıknatısın yerinin
değişimi izlenir.
Eğim Açısı Ölçeri: Eğim açısı kütle merkezinden geçen ve yatay bir eksen
Etrafında dönen bir mıknatıs iğnesi ile ölçülür. Dönme ekseni manyetik alanın
yatay Bileşenine dik olan düşey mıknatıs yardımcı pusula ile döndürüldükten sonra
yardımcı Pusula kaldırılır ve düşey mıknatıs serbest salınıma bırakılır. Düşey
yöndeki mıknatıs yermanyetik alanın toplam bileşeninin etkisi ile onun
doğrultusuna yönelecektir. Bu konumu almış olan mıknatısın yataydan olan sapması
yermanyetik alanın eğim açısını vermektedir.
Gauss Yöntemi ile Manyetik Alanın yatay bileşeninin Ölçümü
Gauss yönteminde kullanılan mıknatısın manyetik momenti M, ve ölçü yerinde
yermanyetik Alanın yatay bileşeni H’dır. Yöntemde MH ve M/H büyüklükleri elde
edilmektedir.
a)MH’nın elde edilmesi (Salınım yöntemi): Mıknatıs askılı sapma açısı ölçerde
olduğu gibi bir tele asılır ve H alanında salınıma bırakılır.
Salınımın peryodu
T=2√I/MH ile verilir.
I= salınım yapan mıknatısın, mıknatısı tutan ve salınan parçanın tümünün atalet
momenti.T periyodu ölçülerek I hesaplanır ve bağıntıdan MH değeri elde edilir.
b) M/H nın saptanması: Yardımcı bir sapma açısı ölçer kullanılır. Buna göre küçük
mıknatıs H yatay bileşeni ile çakışmıştır. Momenti M olan ve KG mıknatısı
saptırma mıknatısı olarak kullanılır. Bunun için KG mıknatıs yatay düzlemde O’dan
geçen her eksen etrafında dönebilen bir çubuğa bağlıdır. Çubuk üzerinde KG
mıknatıs uygun bir OO’=R uzaklığına getirilir. Küçük mıknatıs ile büyük mıknatıs
belli bir açıyla birbirlerine dik olacak şekilde yönlendirilir.
Sin =h/H ve 1. Gauss durumundan M/H= Sin R3/2 buradan H hesaplanır.
Kuvars Yatay Bileşen Manyetometresi
Isı iletkenliği ve burulma katsayısı çok küçük olan kuvars tel, bakırdan yapılmış
bir tüpe asılmış bir mıknatıs kullanılmaktadır. Mıknatısa dik olarak
yerleştirilmiş bir ayna bulunmaktadır.
D dürbünü yaklaşık güneye çevrilir ve manyetometre düşey eksen etrafında
döndürülür ve dürbün ekseni ayna normali ile çakıştırılır. Bundan sonra M
manyetometre düşey eksen etrafında 2+ kadar döndürülür. Ve H=K1/sin
bağıntısından manyetik alan hesaplanır.
Arazide kullanılan klasik Ölçü Aletleri
Schmidt Düşey Bileşen Manyetometre
Yermanyetik alanın H ve Z bileşenleri ölçülür. Bu ölçüler
Bağıl ölçülerdir. Her iki ölçüm için mıknatısın konumlandırılması farklıdır.
Düşey Bileşen Ölçümü:
Manyetometre iki mıknatıstan oluşmaktadır.
KG mıknatısları üçgen prizma şeklinde C kuvars
parçasıyla bağlıdır. Üçgen prizmanın kenarları
CC’ silindirik çubuk üzerine oturmuştur. Bu
şekilde minimum sürtünmeye sahip salınım
yapmaktadır. Vida, somon mıknatısların ağırlık
merkezleri O orta noktası yerine d kadar altta
ve a kadar G kutba kaymış durumdadır. Bu
sistem bir terazi gibi çalışır.
CC’ekseni pusula yardımıyla düşey eksen
etrafında döndürülerek manyetik kuzeye
çakıştırılır. Yermanyetik alanın Z bileşeni
mıknatıslara
±PZ
kuvvet
çiftini
etkilemektedir. PZ manyetik kuvvet çiftidir.
Bu etki düşey alanın bir Zo değeri için yatay
duruma getirilmiş teraziyi yatay durumdan
ayıracak ve K uçları eğilecektir. Manyetik
kuvvet çifti yerçekimi tarafından kaynaklanan
karşıt bir kuvvet etkisi ile dengelenmektedir.
Ölçü yeri değiştirildiğinde teraziye farklı bir Z
alan etki eder. Manyetik kuvvet çifti değişerek
yerçekimi etkisi aynı kalır. Bu nedenle terazi
dengesi yeniden bozulur. Z nin değerine göre
terazi bir yöne sapar.
Modern Ölçü Aletleri
Fluxgate Manyetometresi: Güç kaynağından bobinlere bir elektrik akım
gönderildiğinde büyük manyetik geçirgenliğe sahip çekirdekler eksenleri
boyunca zıt yönde mıknatıslanma kazanırlar. Çünkü bobinler birbirine göre zıt
yönde sarılmışlar.
Birincil
bobinde
alternatif
akım
uygulandığında herbir çekirdek birbirine
göre zıt yönde mıknatıslanır. Birincil
bobinleri saran ikincil bir bobin manyetik
akıdaki bu değişimi kayıt eder. Bu
manyetik
akı
değişimi
çekirdekler
doygunluğa erişir erişmez 0 olur. Dış
manyetik alanın olmadığı bir ortamda güç
kaynağı vasıtasıyla birincil bobine akım
uygulandığında her iki birincil bobinin
ürettiği manyetik alan birbirini yok
edeceğinden
ikincil
bobinde
hiçbir
indüklenmiş akım oluşmaz.
Eğer sensörün ekseni yer manyetik alan doğrultusuna getirilirse, her 0.0005
saniye aralıklarla çekirdeklerden biri diğer çekirdeğe göredaha önce doygunluğa
ulaşır.
Bu durumda çekirdeklerdeki manyetik akının fazları birbirinden farklıdır.
Akı değişimi artık bu iki çekirdekteki gibi eşit ve zıt yönde değildir.
Böylece ikincil bobinde sensörün ekseni boyunca olan yermanyetik alan
bileşeninin kuvveti ile orantılı bir çıkış voltajı elde edilir.
Dış alan ne kadar şiddetli ise, sinyalin genliği o kadar büyük olur.
PROTON
MAĞNETOMETRESİ
silindirik bir kontainer içerisinde
etilalkol ve etrafı bobin ile sarılıdır.
Eğer düğme kapalı tutulduğunda bir doğru akım bobin geçerek
sıvı dolu silindirde güçlü bir mağnetik alan üretmektedir.
Hidrojen atomları uygulanan alan yönüne dizilirler.
Düğmeyi açtığımızda, güç bobinden kesilmektedir. Hidrojen
atomları Yer mağnetik alanın toplam bileşeni yönüne
dizilmektedir.
Proton elektronunun kuvvetli manyetik alanda topaç (prezisyon) hareketi yaptığı
bilinmektedir. Hidrojen atomun kütlesine sahip bir proton, zayıf bir manyetik alan
karşısındaki davranışı uzun eksen etrafında dönme hareketi yapan bir çubuk
mıknatıs hareketine benzemektedir. Proton bir taraftan mıknatıs
özelliğinedeniyle bulunduğu yermanyetik alan vektörünün doğrultusunu almaya
çalışırken, kendi ekseni etrafında yaptığı dönme hareketi nedeniyle istediği
yönelmeyi hemen sağlayamaz. Bu nedenle protonun manyetik momenti protonun
bulunduğu noktadaki manyetik alan vektörü etrafında topaç hareketi yapmaya
başlar.
Proton manyetometresinde sözü edilen topaç hareketinin frekansı ölçülür. Topaç
hareketin frekansı ise protonun içinde yer aldığı manyetik alanın şiddeti ile doğru
orantılıdır. Manyetik alan ne kadar şiddetli ise, topaç hareketinin frekansı o
kadar büyük olur.
F=H/2a ; f=Larmor frekansı ; /a=protun manyetik momenti
Protonun manyetik momentinin protonun kinetik momentine oranı
p=Gyromanyetik oran olup=0.267513 (-saniye)-1’dir.
Böylece bağıntıda
F= pH/2 buradan hareketinin açısal frekansı w= pH olarak elde edilir. Bu ise
protonun içinde bulunduğu manyetik alan şiddeeti ile doğru orantılıdır.
Yer manyetik alanın şiddeti İstanbul’da H=0.466 Oe 46600 nT olduğuna göre
proton manyetometresinin ölçtüğü frekans 1984 Hz olmalıdır.
Çalışma Prensibi
Aletin algılayıcıs manyetik olmayan malzemeden yapılmıştır. İçi etilalkol ,
metanol gibi hidrojen bakımından zengin bir sıvı ile doldurulmuştur. Silindirik
kabın dışına ince telden bir bobin sarılmıştır. Bu bobine doğru akım
uygulandığında bobinin oluşturduğu manyetik alan bobin ekseni doğrultusunda
olur. Şekilde gösterildiği gibi yer manyetik alan olmasına rağmen kap içindeki
protonların herbirinin manyetik momenti gelişigüzel.
Algılayıcı bobin etrafındaki bobine doğru akım verildiğinde algılayıcı bobin
etrafındaki sarım sayısı 4.5 voltluk pil bile kullanılsa, birkaç saniye bobinin
eksen doğrultusunda 50-100 Oe lik manyetik alan meydana gelmektedir.
Bobinin uyguladığı bu manyetik alan ölçülmek istenen yermanyetik alanın birkaç
yüz katıdır. Bu yüzden algılayıcı içindeki bütün protonlar manyetik
momentlerini bobin ekseni doğrultusuna yönlendirirler.
Algılayıcı etrafındaki bobine uygulanan doğru akım kesildiğinde iki değişiklik
olur.
a) Algılayıcı kap etrafına sarılı olan bobin görev değiştirerek frekans sayma
devresinin bir elemanı haline dönüşür.
b) Birkaç salise önce manyetik momentlerini algılayıcı bobin ekseni etrafında
yönlendirmiş olan protonlar kuvvetli dış alan kalktığında manyetik
momentlerini ortamda var olan zayıf yer manyetik alan vektörü yönünde
yönlendirmek ister. Bu durum 1 sn. gibi kısa bie zamanda topaç hareketi
yapmasına dayanmaktadır.
Optik Pompaj Manyetometresi (Sezyum Rubidyum Buhar Manyetometresi)
Optik pompaj radyasyon veya radyo frekansındaki EM dalgalar yardımı ile bir
elementin bazı elektronlarının belli bir enerji düzeyine getirilmesi veya
yükseltilmesidir. Optik pompaj manyetometresi proton manyetometresinde
olduğu gibi içinde bulunduğu manyetik alanın şiddetini ölçer. Manyetik alan
vektörünün yönü hakkında bilgi vermez.
Proton manyetometresinde protonların yaptıkları topaç hareketinin frekansı
ölçülürken, optik pompaj manyetometresinde elektronların topaç hareketine ait
frekans ölçülür.
Her elementin bünyesinde bulunan elektronların topaç hareketinin frekansını
ölçmek mümkün değildir. Bunun için en uygun element Sezyum ve Rubidyumdır.
Şekilde Sezyum buhar manyetometresi görülmektedir.Flamanı sezyumdan
yapılmış ampulden çıkan ışık bir ince kenarlı mercek ve onu izleyen polarizörden
geçtikten sonra sezyum buharı ile dolu bir hacme girmekte ve buradan çıkan
ışık ince kenarlı mercekten geçerek ışık şiddetindeki değişimlere karşı duyarlı
olan fotoelektrik tüpe ulaşmaktadır. Fotoelektrik tüp değişik frekanslarda
alternatif akım üreten bir üreteç ile bağlantılı olup, bu üreteç tarafından
istenilen frekansda üretebilen AA, sezyum buharı ile dolu hacim etrafıan
sarılmış bobin vasıtasıyla ortamda belli frekansda manyetik alan
oluşturabilmektedir.
Sezyum buharını oluşturan atomların valans elektronları sahip oldukları
enerji düzeyine göre farklı yörüngeler işgal eder. Şekilde en küçük
enerjiye sahip valans elektronu A2 yörüngesini en büyük enerjiye sahip
olan valans elektronu B1 yörüngesini işgal etmektedir.
Düşük enerji yörüngesinde bulunan bir elektron ortamdan geçmekte olan sezyum
ışığı fotonlarını absorbe ederek sahip olduğu enerjiyi giderek arttırır.
Ve enerjisini belli bir düzeye yükselttiğinde üst valans yörüngesine kaçabilir.
Elektronların sıçrayabileceği yörüngeler önceden bellidir. Örneğin A2 ve A1
yörüngelerini işgal etmekte olan iki elektron yeterli miktarda enerji
aldıklarında sırası ile B2 ve B1 yörüngelerine yükselebilir. Optik pompajın bu
aşamada sezyum ışığı fotonları ortamdaki elektronlar tarafından adsorbe
edildiğinden sezyum buharını geçip fotoelektrik tüpe ulaşan ışığın parlaklılığı
bir miktar azalır.
Sezyum buharını oluşturan atomların
A1 yörüngesinde bulunan
elektronların hepsi B1 yörüngesine geçtiğinde ortamdan geçmekte olan
sezyum ışığı fotonları adsorbe edilemez ve fotoelektrik tüpe ulaşan
ışığın parlaklığı artar.
Fotoelektrik tüp bu değişikliği algıladığında alternatif akım üreteci
çalışmaya başlar. Böylece sezyum buharının bulunduğu hacme, frekansı
zaman içinde değişen manyetik alan uygulamaya başlar. Alternatif akım
üreteci ürettiği akımın frekansını, elektronun topaç hareketinin
frekansını yakalayıncaya kadar değiştirir. Bu kritik frekans değerine
ulaştığında A2 yörüngesinde bulunan elektronlar A1 yörüngesindeki boş
pozisyonları işgal ederler.
A1 valans yörüngesine çıkan elektron anında ışığı absorbe edecek ve sezyum
buharı tüpünden geçip foto elektrik tüpe ulaşan ışığın şiddeti azalacaktır.
Alet bu ikinci ışık azalmasına neden olana alternatif manyetik alanın
frekansını kaydeder.
Manyetik alan şiddeti T= 2/e )v ile hesaplanır.
Arzmanyetik Alanın Esas veya Ortalama
Alan Bileşeni
Arzmağnetik alanı arz yüzeyine dağılmış mağnetik gözlemevlerinde sürekli
olarak ölçülmektedir. Şekil’de arz yüzeyindeki yaklaşık konumları görülen bu
gözlemevlerinde, mağnetik alanın genellikle {X, Y, Z} veya {D, H, Z} bileşenleri
variyometreler ile sürekli olarak kaydedilmekte ve birçoğunun da alanın
toplam bileşeninin mutlak değeri, son yıllarda geliştirilen proton
magnetometreleri ile çok kısa aralıklarla sayısal olarak elde edilmektedir.
Gözlemevlerinin arz yüzeyindeki dağılımı
Şekil’de ise, bu gözlemevlerinden birinde kayıt edilen
magnetogram’a örnek gösterilmiştir.
ORTALAMA ALAN
Mağnetik gözlemevlerinde sürekli kayıt edilen arzmağnetik
alanının herhangi bir bileşenini ele alıp, örneğin alanın toplam
bileşenini, bu bileşenin saatlik değerlerinden yararlanarak,
bağıntısı ile toplam bileşen için günlük ortalama değerini bulabiliriz.
Bir ay içindeki günlük ortalama değerlerden,
bağıntısıyla aylık ortalama değeri ve
bağıntısıyla da alanın ele aldığımız toplam bileşeni için yıllık ortalama
değerine ulaşabiliriz.
Bu değere ulaşılırken, gerek ulaşılan değerin mertebesinden ve
gerekse de gözlemevinin yeri seçilirken öngörülen şartların (magnetik
anomali verecek yerlerden uzak olma gibi) yerine getirilmelidir.
Ancak, herhangi bir gözlemevinde , alanın yıllık ortalama değeri uzun bir
süreçte izlendiği zaman,
bu değerin
Yıllara göre sabit olmadığı,
Periyodu uzun sayılabilecek bir değişimin katkısı da içerdiği görülebilir
(Şekil).
Şekil 5.3 a’dan izlendiği gibi t1 den
tn yıla doğru alanın sözü edilen yıllık
ortalama değerinde sürekli bir
artış görülmektedir. Bunun yanı sıra,
bu değişime uyabilecek uygun bir
fonksiyon (doğrusal veya eğrisel)
geçirildiği zaman, bu fonksiyonla,
gözlenen değişim arasındaki farkın ,
yıllara göre periyodik bir değişim
gösterdiği de dikkati çeker
(Şekil5.3b).Bu periyodik
değişiminde, güneş faaliyetlerinin
bir göstergesi olan ve R ile
gösterilen güneş leke sayılarının
değişimi ile yakın bir ilişki içinde
olduğu da görülür.
Bu nedenle, t1 ile tn arasında, alanın herhangi bir tr yılındaki değeri
ele alınmak istendiğinde, yukarıda sözünü ettiğimi değişimlerin
etkilerinin tr yılındaki değerden arındırılması istenir. Bu değere de;
Ftr = (Ftr-4 + … + Ftr-1 + Ftr + Ftr+1 + … + Ftr+5 )/10
(5.4)
bağıntısıyla ulaşılır. Doğrusu, tr yılındaki mağnetik alan değeri
alınmak üzere (örneğimizde toplam bileşen), bu yıldan 4 yıl öncesi
ve 5 yıl sonrası değerleri toplanıp 10’a bölünmek suretiyle,
arzmağnetik alanının tr yılındaki değeri bulunur.
Bu değere arzmağnetik alanının o gözlemevi için ortalama veya normal
alan değeri denilir. Bu değer yalnızca arz içince geçen olaylara bağlı
olarak değişir. Bu nedenle, esas alan adı da verilmektedir.
Eğer, mağnetik gözlemevimizde birkaç yıllık (10 yıldan az) ortalama
değerimiz var ise, bu halde, önce yıllık ortalama değerler, zamanın
fonksiyon olarak grafiklenir (Şekil 5.4).
Manyetik Değerlerin Belirli Bir Zamana İndirgenmesi
Anlaşılacağı üzere, esas veya ortalama alanı bir yerde saptamak için,
orada, hiç olmaz ise, belli bir sürede alan ölçüsü almak
gerekmektedir. Ancak, bunun için her zaman, ele alınan yerde
mağnetik bir gözlem yeri de gerekli değildir. Genellikle değişik
gözlem yerlerinden gelen kayıtlar (magnetogramlar) incelendiği
zaman, görülür ki aralarındaki uzaklık yüz kilometre civarında olan
yerlerdeki mağnetik değişimler arasındaki farklar yok sayılacak
derecede azdır. Bu ilkeye dayanarak; bir gözlem yerinde herhangi
bir t anında toplam bileşen F nin değeri
olarak yazılabilir. Fy , t anından önceki 10 yıllık döneme ait ortalama
alan değeri ve ∆Ft de Ft ve Fy arasındaki farktır. Gözlem yerine
yakın, bir diğer yerde ise aynı t anındaki değerler , aynı şekilde
şeklinde ifade edilebilir. ∆ Ft ≈ ∆Ft’
olduğundan
bağıntısına, (yukarıda verilen bağıntılardan geçilebilir. Bu bağıntı
ile bir diğer gözlem yerinde t anında Ft’ değerini ölçmekle alanın
ortalama değerine geçmek mümkündür. Bu işleme indirgeme adı
verilir.
ORTALAMA ALANIN UZUN SÜRELİ
DEĞİŞİMİ
Ortalama veya esas alan zamanla sürekli
gelişme gösterir. Arzmağnetik alanının
seküler değişimi adını alan bu gelişme
önemli bir olaydır. Kaynağı arzın içinde
olan
bu
değişimi,
ayrıntıları
ile
anlayabilmek için, mümkün olduğu ölçüde
dünyanın her yöresinden sağlanmış, çok
sayıda ve uzun süreli mağnetik ölçüm
sonuçlarına gereksinim vardır. Şekil de
Paris
ve
Londra’daki
kayıtlardan
yararlanarak mağnetik alanın sapma ve
eğim açılarının değişimi 16. yüzyıl
ortalarından bu yana görüntülenmiştir.
Paris ve Londradaki sapma ve eğim açılarının değişimi
Şekil de ise, İstanbul’da sapma açısının, 1600 yılından
günümüze, değişik yıllarada ölçülmüş değerlerinden çıkarılan
değişimi gösterilmiştir (Özdoğan ve diğerleri, 1981).
Istanbuldaki sapma açısının 1600 yılından bu yana
değişimi
Şekli izlediğimizde, sapma açısı 16001750 yılları arasında, artan değerlerle,
batıya yöneliktir. 1750 yılından günümüze
kadar da, sürekli doğuya doğru gelişim
göstermiştir.
Alanın uzun süreli bu
değişimini,
diğer
bileşenler üzerinde de
izlemek
olanaklıdır.
Örneğin,
Şekil’de
,
Japonya’daki
Kakioka
gözlemevinde, 1900-1950
süresinde, alanın X, Y ve
Z bileşenlerinin değişimi
görülmektedir.
Kakioka gözlemevindeki arzmağnetik alanın X, Y, Z
bileşenlerinin yıllara göre değişimi
Şekil’de ise, İstanbul’da, 1911-1947 yılları arası ölçülmüş,
manyetik alanın H ve Z bileşen değerlerinin değişimi
görüntülenmiştir.
Bu şekilde birçok manyetik gözlemevleri için de elde edilen seküler
değişim eğrilerinden, değişimin şekli hakkında bir sonuç çıkarılması
arzu edilir. Ayrıca değişimin şekli hakkında ileriye dönük tahminler
yapılması amaçlanır. Bu da belirli bir süre aralığı için elde edilen
değişimin genel davranışının, aynı uzunluktaki diğer bir süre aralığı
için beklenmesi olasılığına dayanırsa da, gerçek buna uymayabilir.
Seküler Değişim
Yerin
herhangi
bir
noktasında
jeomanyetik alan zamana göre sabit
değildir. Zamana göre alandaki bu
değişimlere
seküler
değişim
denilmektedir. Bu değişimler hem dipol
hem dipol olmayan alanda görülmektedir.
Ortalama Alanın Arz Yüzeyinde İncelenmesi
Daha önce değinildiği gibi, arzmanyetik alanı yalnız zaman göre
değil yere göre de farklılıklar gösterir. Bu durumda herhangi bir
dönem için elde ettiğimiz ortalama alanın arz’ın değişik yerlerinde
değişik özellikler göstermesini beklemek doğal olacaktır. Alanın arz
yüzeyindeki dağılımının incelenebilinmesi, şüphesis aynı bir tarihe
indirgenmiş manyetik alan değerlerini ( alanın herhangi bir
bileşeninin) uygun ölçekli bir haritaya geçirip, eşdeğer noktalarının
arasını sürekli bir eğri ile birleştirerek yapılır. Bu şekilde hazırlanan
haritalara manyetik haritalara denir. Burada, mağnetik haritaların
elde edilip, incelenmesi
Memleket ölçüsünde
Dünya ölçüsünde olmak üzere iki grupta yapılacaktır.
MEMLEKET MANYETİK HARİTALARI
TREND ANALİZİ
Memleket Manyetik Haritaları
Milli sınırlar içerisinde kalmak üzere, bölgesel (rejyonal) ölçekli
haritalardır. Bu haritaların yapımı söz konusu olduğu zaman, ölçü
noktaları, diğer adı ile, istasyon aralıkları en fazla 10-20 km arasında
olmak üzere seçilir. Yalnız istasyon seçimi özel bir dikkat ister,
seçilecek ölçü yeri yakınında, yüksek gerilim hatları, beton bina ve
benzerleri olmamalıdır. Ölçü yerleri tren yolu veya ana yoldan oldukça
uzak seçilmeli ve ölçü alınan yerler, manyetik anomali verecek
kütlelerden uzak seçilmelidir. Eğer bozucu bölge bulunur ve bu bölge
geniş bir alana yayılmış ise, bu bölgeden eşdeğer eğriler geçirilirken, bu
eğriler sürekli değil kesikli veya noktalı eğriler şeklinde geçirilir.
Genellikle arazide (D,H,Z) veya (X,Y,Z) bileşenleri ölçülür. Bu
değerler belirli bir tarihe indirilir. Bu işlem alanın dış kaynaklı
bileşeninin etkisini yok etmek anlamını da taşır. İndirilen değerler uygun
ölçekli bir haritaya geçirilir. Böylece, eşdeğer noktaların
birleştirilmesiyle, ölçülen bileşen için indirilen tarihin manyetik haritası
yapılmış olunur.
Memleket ölçüsündeki bu ölçüler, belirli aralıklar ile yenilenir. Bu 5,
10 veya 20 yılda bir olmak üzere yapılabilir. Her dönem için ölçü
değerleri yine belirli bir tarihe indirilir. Yalnız ölçüler yenilenirken, bu
kez ölçü noktaları10-20 km değil, daha fazla alınır.
Bu haritalar hazırlandıktan sonra, memleket sınırları içinde esas
alanın dağılımını bilmek gerekir. Bu dağılımın belirli aralılarla bilinmesi,
şüphesiz bize esas alanın bölgesel ölçekte zamanla değişimini
inceleyebilme olanağı vermesinin örtesinde, belli bir epok için esas
alanın dağılımının bilinmesi, memleket ölçüsünde veya bölgesel ölçekte
anomali haritalarının yapılabilmesini de sağlar.
Memleket ölçüsünde esas alanın dağılımını bulmak için her bir ölçülen
bileşen için enlem ve boylama bağlı olarak değişen, birinci veya
genellikle ikinci dereceden bir denklem yazılır. Birinci veya ikinci
dereceden olabilecek bu denklemler;
F = b 0 + b 1 . x 1 + b2 . x 2
(5.10)
F = b0 + b1 . x1 + b2 . x2 + b3 . x12 + b4 . x22 +b5 . x1 . x2
(5.11)
ile ifade edilir. Bağıntılarda b0 , b1 ,……., b5 saptanması gereken katsayılar, x1 ve
x2 her nokta için ölçü noktalarının enlem ve boylamını belirlerler. Bu katsayılar;
her nokta için ölçü nokta için ölçülen mağnetik alan bileşenleri (X,Y,Z,H,F) ve bu
noktaların enlem (x1) ve boylamı (x2) bilindiğine göre, en küçük kareler yöntemi
(E.K.K.Y.) ile bulunur. Daha sonra, (5.10) veya (5.11)’e göre her nokta için esas
alan değeri belirlenir. Bu işlem, istatistikte Trend analizi olarak da bilinir.
Lineer doğrudan olan farklar
Şekil’de bağımsız değişken sayısına göre y ve x (bir veya birden çok)
nin belirlediği dağılıma uyabilecek doğrusal ve eğrisel trend
fonksiyonları ile, doğrusal veya eğrisel trend yüzeyleri
görüntülenmiştir.
Hemen dikkat edilecek olursa, tek bağımsız değişken olduğu zaman
1. veya 2. dereceden bir polinom, iki bağımsız değişken olması halinde 1.
veya 2. dereceden bir polinom yüzeyine dönüşmektedir. Buradan
bağıntıları ile verdiğimiz denklemlerin nasıl bir trend yüzeyi
oluşturdukları da ortaya çıkmaktadır.
F = b0 + b1 . x1 + b2 . x2 ve
F = b0 + b1 . x1 + b2 . x2 + b3 . x12 + b4 . x22 +b5 . x1 . x2
bağıntılarında x1 ve x2 bağımsız değişkenler olmak üzere, o
noktadaki enlem ve boylamın fonksiyonu olan toplam bileşen için
arzmağnetik alanının kaynağına göre esas alan bileşenini
belirleyecek katsayılar, n veri için ;
1. dereceden trend yüzeyi
∑F = nb0 + b1 ∑ x1 + b2 ∑ x2
∑x1 F = b0 ∑ x1 + b1 ∑ x12 + b2 ∑ x1 x2
∑ x2 F = b0 ∑ x2 + b1 ∑ x1 x2 + b2 ∑ x22
Benzer şekilde, (5.11)’e göre ikinci dereceden bir trend yüzeyini
belirleyebilmek için, sayısı 6 olan bir normal denklem takımı oluşturulur.
Bu denklem takımının çözümüyle istediğimiz katsayılar elde edilir.
(5.10) ve (5.11) bağıntılarından her x1 ve x2 (enlem, boylam) için elde
edilen değerler, bizim istediğimiz her nokta için esas alan değerlerini
vereceğinden, enlem ve boylamı ( x1 ve x2 ) belirli noktada ölçü
değerimiz ile hesapladığımız değerle olan fark, bize esas alanın tüm
ülke üzerindeki dağılımı, hem de memleket ölçüsünde mağnetik anomali
haritaları elde edilmiş olur.
Şekil de görülen, herhangi bir harita alınarak, bu haritadaki verilere
uyan birinci dereceden bir trend yüzeyi
ve bu yüzeyden olan fark (anomali) haritası Şekil de gösterilmiştir.
Şekil de ise, aynı haritaya uyabilen ikinci dereceden bir trend yüzeyi
ve anomali haritası gösterilmiştir.
Türkiye için Harita Genel Komutanlığınca yapılan ölçüler sonucu
arzmağnetik alanının esas alan bileşeninin, yukarıda sözü edilen
yöntemle elde edilerek, seküler değişimi, H (yatayı) ve D(sapma açısı)
bileşenleri için şekil 5.13 ve şekil 5.14 te gösterilmiştir (İspir ve
diğerleri,1975).
DÜNYA MAĞNETİK HARİTALARI
Dünya ölçüsünde mağnetik haritaların yapımı bazı özel kayıtları öngörür.
Bunun için dünyanın her tarafında aynı bölge ve aynı dönemler ait
mağnetik ölçülerin elde bulunması gerekir. Fakat eldeki ölçüler
heterojendir. Bazı sık aralıkları olan yerlerde çok sayıda ölçüler vardır.
Bazı yerlerde (Büyük çöl, Okyanuslar ve kutuplar gibi) ya hiç değer
yoktur yada sayıları azdır. İçinde bulunduğumuz yüzyılın başından
buyana dünya ölçüsünde büyük çaba harcanmış önce Carnegie
Enstitüsünün (A.B.D.) çabaları ile Galilei ve Carnegie adlı mağnetik
olmayan maddeden yapılmış gemiler, sonrada jeofizik yılı içerisinde
(1957-58) 15 ay süre ile Rus yapımı Zanya yardımı ile Okyanuslarda ve
kutuplara yakın yerlerde ve ayrıca da havadan yapılan ölçülerle boşluklar
doldurulmak istenmiştir (Özdoğan, 1971).
Yukarıdaki açıklamadan da anlaşılacağı gibi ölçüler çok değişik
zamanlarda yapılmıştır. Bu nedenlerden bu ölçülerin, aynı bir tarihe
indirilmesi çetin kavram ve hesap güçlükleri ortaya koymuştur. Dünya
jeofizikçilerinin ortak çalışmalarıyla arzmağnetik alanının zamanla
değişmeleri ve arz yüzeyindeki dağılması, çok ince olarak gözden
geçirilerek, dünya mağnetik haritasının yapımı tamamlanmıştır. Bugün bu
haritalar her 5 yılda bir (tam onda yıllardan başlayarak)
yenilenmektedir.
Dünya Mağnetik Haritasının Karakteri İzoklinler:
Meyil açısından eşdeğer eğrileridir. Bunlar yaklaşık olarak paralelleri izlerler. I =
0 değerini taşıyan izoklin, mağnetik ekvator adını alır. Bu eğri , birisi Atlantik
Okyanusunun ortalarında (25 ° W) ve diğeri pasifik Okyanusunun ortalarında (165
°W) boylamlarında olmak üzere coğrafi ekvatoru iki yerde keser. Orta Afrika ya
yakın yerlerde coğrafi ekvatorun 10° üstünde ve Güney Amerika üzerinde ise 15°
güneyinden geçer. Mağnetik ekvator küremizi ikiye böler (Şekil).
kuzeyde I > 0 ve güney yarımkürede I < 0 dır. Mağnetik ekvatordan
başlayarak kutuplara doğru ilerledikçe meyil açısının mutlak değeri
artmaya başlar, izoklinler bir nokta çevresinde sıklaşırlar, bu sıklaşan
eğrileri ortak merkez kabul edecek nokta I = 90° olan yerdir ki buraya
mağnetik kutup veya meyil açısı kutbu adı verilir.
1947 yılında bu kutupların yerleri, kuzey mağnetik kutup
73° K ve 100 ° B ile güney mağnetik kutup 68,7°G ,143 ° D idi.
1965 yılı değerleri ise 75,5 ° K, 100,5 °B ile 66,5 ° G ,139,9 ° D dir.
Görülüyor ki güney ve kuzey mağnetik kutuplar bir küre çapının
uçlarına rastlamamaktadır.
.
İzogonlar:
Coğrafi ve mağnetik kutuplara doğru yönelmişlerdir. Bu noktanın çevresinde
sapma açısı 0° ile 180° D ve 180° B arasında her değeri almış olacaktır.
Coğrafi ve mağnetik meridyenelrin çakıştığı noktalardan geçen izogon, 0° ve
180° izogonlarıdır ki arzımızı kutuplardan geçerek çevreler. Bozuk bir eğri
olan bu izogonlar arzı iki yarım küreye ayırır. Biri Atlantik Okyanusunu
kapsar. Orada D’nin değeri batı, diğeri Pasifik Okyanusu bölgesindedir ve
orada da sapma açısı doğrudur.
D = 0° olan uzun izogonlar, agonik adını alır. Agoniklerden kimi kuzey
mağnetik kutuptan başlar (Şekil). Kuzey ve güney Amerika dan geçer ve
güney coğrafi kutuptan başlar. Skandinav memleketlerinden ve
Yunanistan dan geçerek Aden körfezien uzanır. Hindistan, Sibirya
yoluyla Kuzey denizine erişir. Oradan Asya yı çevreleyerek Güney
mağnetik kutupta sonlanır.
İzomağnetikler:
İzomanyetik H lar izoklinlere benzer. Mağnetik kutuplara doğru sürekli
zayıflar. Sonunda izomağnetikler mağnetik kutbu çevreler. Burada H =
0’dır. Yatay bileşen değeri ekvatora doğru artar ve bir maksimumdan
geçer. H’ın maksimum değerinin mağnetik ekvator üzerinde bulunmaları
zorunlu değildir (Şekil).
İzomağnetik Z’lerde, izoklinlere benzer. İzomağnetik, Z = 0
mağnetik akvator adını alır. Kuzey yarımkürede Z > 0, güneyde Z < 0
alınır. Mağnetik ekvatordan kutuplara gidildikçe Z büyür (Şekil
5.18).
İzomağnetik toplam alan, Z haritaları görüntüsündedir.
İzomağnetiklerin değerleri ekvatordan yüksek enlemlere gidildikçe
artar (Şekil 5.19).
Sonuç olarak görülüyor ki arzın mağnetik alanının arz yüzeyi
üzerindeki dağılımı çok karışık görünmemektedir. Gilbert devrinden
beri (1600 yılından) bu dağılımın, düzgün mıknatıslanmış bir küre
üzerindeki alanının dağılımına benzediği fakat yer yer düzgünlüğünün
bozulduğu, şahısların gözünden kaçmamıştır. Arz yüzeyinde
izlediğimiz alanın ayrışımı yapılmakla düzgün alan ve bu alanda
kıyaslama yoluyla da arz alanının anomalisi denetlemek mümkün
olacaktır.
YER MANYETİK ALANI
KÜRESEL HARMONİK ANALİZ
KÜRESEL HARMONİK ANALİZ
Laplace eşitliği
Gerilmiş bir bant ve bbuna y doğrultusunda bir kuvvet uygulandığını göz önüne alalım. Lastik
bandın y doğrultusunda yer değiştirmesi () aşağıdaki diferansiyel eşitlik ile gösterilir.
∝
𝑑2∅
𝑑𝑥 2
= −𝐹(𝑥)
; (α=sabit)
F(x)=x doğrultusundaki birim uzunluk başına y doğrultusuna uygulanan kuvvet’dir.
Eğer F(x)=0 ise;
Kuvvet uygulanmaz ise, band düz bir doğrultuda kalır. Ve
𝑑2∅
𝑑𝑥 2
= 0 olur.
Bir fonksiyonun 2. Türevi o fonksiyonun eğriliğini ölçer. Buna göre gergin bir banda bir
kuvvet uygulanmazsa, herhang bir eğrilik-kavislenme göstermez. Bu basit şekilde Laplace
eşitliğinin 1-B’lu şeklidir. Fakat 2 ve 3-B’lu duruma açılabilen harmonik fonksiyonların
önemli bir özelliğini göstermektedir.
Lokal minimum ve maksimum noktalarda Laplace eşitliği sağlanmaz. Bu örnekte Laplace
eitliğinin sağlanması için maksimum ve minimum yerdeğiştirme lastik bandın başlangıç ve
bitiş noktasında olması gerekmektedir.
Harmonik fonksiyon
1. İki değişkene sahip bir fonksiyonun herhangi bie noktadaki değeri o nokta etrafındaki
bir dairenin etrafoındaki ortalama değerine eşittir. Bunu sağlayan fonksiyon bu
dairenin içerisinde tanımlanır. Sonsuz sayıda nokta bu ortalama içerisinde olabilir. O
zaman bu integral yardımıyla çözülür.
2. Fiziksel anlamda harmonik fonksiyonlar geniş bir alanda sıcaklık, alan veya elektrik
yük dağılımındaki denge durumunu tarif eder.
3. Harmonik fonksiyonlar aynı zamandaLaplace eşitliğini sağlayan fonksiyonlar olarak
göz önüne alınır. Harmonik fonksiyon ile tanımlanan yüzey 0 konveksiviteye sahip
olup bölge içerisinde maksimum ve minimum değerleri yoktur.
4. Harmonik fonksiyonlar analitik olup, tüm türevlere sahip (yani mükemmel şekilde
pürüzsüz) güç serileri diye adlandırılan sonsuz sayıda terimlerden oluşan polinomlar
ile gösterilir.
Küresel harmonik fonksiyonlar küresel koordinat sistemi kullanıldığında ortaya çıkar. Bu
sistemde uzaydaki bir nokta üç koordinat ile tanımlanır. Bir tanesi orjinden olan uzaklık, diğer
ikisi enlem ve boylam açısını verir. Küresel koordinatlar gravite, manyetik, elektrik alan gibi
3B’lu alanları tanımlamak için kullanılır.
En basit harmonik fonksiyon koordinatları (a,b,c) ve (X,y,z) olan iki nokta arasındaki
uzaklığın tersi olan
1
1
𝑢
Fonksiyonudur.
=
(𝑥 − 𝑎)2 + (𝑦 − 𝑏)2 + (𝑧 − 𝑐)2
Yermanyetik Alanın Küresel Koordinatlarda Gösterimi
Yeryüzeyinde manyetik alanın yericinde bir dipolün meydana getirdiği alan ile birlikte benzer
olduğunu anlamak için küresel harmonik fonksiyon analizini bilmemiz gerekir.
Maxwell denkleminden
x B=J +
𝜕𝐷
(J=elektrik akım yoğunlupu;
𝜕𝑡
𝜕𝐷
𝜕𝑡
= elektrik akım yoğunluğu deplasmanı)
Yeryüzünden 50 km yüksekliğe olan bölge elektromanyetik boşluk olarak kabul edilir. Bu
bölgede J=0 ve
𝜕𝐷
𝜕𝑡
= 0’dır. Buradan x B=0 şeklini alır. Rotasyonu 0 olan alan konservatif
bir vektör alandır ve bu alanıın V skaler gibi bir potansiyeli vardır.
Eğer x B=0 yani curl B=0 ise B=-grad V ; div B= .B=0
Div (-gradV)= 2 V=0 şeklinde V potansiyeli Laplace bağıntısını sağladığı görülür.
Küresel koordinatlarda (r, ,) olmak üzere r yerkürenin merkezinden olan radyal uzaklık, ,
co-latitüd açısı, ise boylam açısı olmak üzere tanımlanır.
KÜRESEL HARMONİK ANALİZİ İÇİN 3 FONKSİYON TANIMLIYORUZ
r’li değişkene ait fonksiyon: Yerin iç ve dış alanı ile ilgili
’li değişkene ait fonksiyon: 0-2 arasında boylama bağlı periyodik
fonksiyon
’lı değişkene ait fonksiyon:Legendre fonksiyonu olup Pnm(), enleme ait
bilgi vermektedir.
Boylamın Periyodik Gösterimi
Periyodik bir fonksiyonun 1-B’da gösterimi
Herhangi bir f(t) fonksiyonu bir T aralığında periyodik ise bu fonksiyon (m
dalga sayıları ie birlikte) sinozoidlerin toplamından oluşur. Bunu gösteren
teknik Fourier analizidir.
Sinuzoidal fonksiyonlar ortogonaldir. Yani bir T aralığında integrali
alınırsa 0 olur. İki temel fonksiyon özdeş olmadığı sürece örneğin;
Ortogonalite: Bu terim vektörlerle çalışıldığında karşımıza çıkar. İki
vektör birbiriyle 90olik açı yapıyorsa ortogonaldir. O zaman iki vektörün
skaler çarpımı 0’dır.
Bir fonksiyonun ortalamasına bakıldığında + ve – kısımdan oluştuğu
görülür.
Şekildeki alanın integrali alınırsa;
2𝜋𝑘
𝑠𝑖𝑛𝑤𝑡 𝑑𝑡 = 0
0
Bir boylama ait bir daire etrafında f(t) peryodik bir fonksiyon düşünelim; t
yerine boylamı () yazalım T=2 olsun.
∞
𝑓 ∅ =
𝑎𝑚 𝑐𝑜𝑠𝑚∅ + 𝑏𝑛 𝑠𝑖𝑛∅
𝑚 =0
Bu seriler tüm co-latitüdlerde boylama ait fonksiyonları tanımlar. O
zaman
∞
𝑓 𝜃, ∅ =
𝑎𝑚 (𝜃)𝑐𝑜𝑠𝑚∅ + 𝑏𝑛 (𝜃)𝑠𝑖𝑛∅
𝑚 =0
Co-latitüde ait Fonksiyonlar (Co-latitude açısı enlem açısınnı 90
dereceye tamamlayan açıdır)
Küre üzerinde co-latitüde ait fonksiyonlar boylam için olan gibi periyodik
olmak zorunda değildir. Bunun için boylamda kullanılan basit sinuzoidler
iyi bir seçim değildir. Küre üzerinde enlem değişimini göstermek için
ortogonalite temeline dayanan fonksiyonlara ihtiyaç vardır. Değişken
ayırımını çok iyi temsil etmesinden dolayı Legendre fonksiyonları colatitüdü göstermede en iyi yoldur.
Legendre Polinomları
Yukarıdaki üçgende u kenarı diğer iki kenar (r ve R) ile açısıyla
ilişkilidir. 1/u ifadesi cosinüs kanunu ile yazılabilir.
1
1
= 2
𝑢 (𝑅 + 𝑟 2 − 2𝑟𝑅𝑐𝑜𝑠𝜃)1/2
(r/R) ile verilen yukarıdaki sonsuz uzunluktaki terim uzaklık formülü olup,
kısaca aşağıdaki gibi yazılabilir.
1 1
=
𝑢 𝑅
∞
𝑛=1
𝑟
𝑅
𝑛
𝑃𝑛 (𝑐𝑜𝑠𝜃)
açısı r ile referans kenar R arasındaki açısal farkdır. 𝑃𝑛 (𝑐𝑜𝑠𝜃) n.
Dereceden Legendre polinomudur. Herbir polinom (r/R)n
‘in bir
katsayısıdır. Bu polinomlar 1/u’nun sonsuz sayıda ortalamasıdır. Eğer
cos=x ve 𝑃𝑛 𝑐𝑜𝑠𝜃 = 𝑃𝑛 (𝑥) ise ilk polinomlar n=0,1,2 ve 3 için:
P0(x)=1
3𝑥)
P1(x)= x
1
P2(x)= (3𝑥 2 − 1)
2
1
𝑃3 𝑥 = (5𝑥 3 −
2
Enlem
değişimleri
veren
Legendre
fonksiyonları
ile
boylamdaki
değişimleri veren Fourier serileri birlikte genel çözüm içerisinde
verildiğinde;
Elde edilir.
Uzaklık ile ilgili değişkenler
Yeryüzeyinde Laplace eşitliğinin çözümü yermanyetik alanın mümkün
alabilen iki kökeni ve alanı meydana getiren potansiyeli içermektedir.
Alanın aslında iç ve dış olmak izere 2 kökeni vardır. Bu yüzden analiz
sonucu elde edilen katsayılar potansiyele iç ve dış kaynaklı katkı olarak
ifade edilir. Bunun anlamı dış kaynaklı alan iç kaynaklı alana
yeryüzeyinde ölçülen bir değeri vermek üzere ilave olur. Laplace’ın sınır
şartlarının sağlanması için dış kaynaklı bir alan yeryüzeyinde büyük
uzaklıklarda oluşturulmalı. Ayrıca alanın büyüklüğü de yerküre içerisinde
yeryüzeyinden yerin merkezine doğru azalarak tam merkezde 0 olur.
Bunun göstergesi
𝑟
( )𝑛 ’dir.
𝑎
𝑎
İç kaynaklı manyetik alan r’ye ( )𝑛+1 şeklinde gösterilir.
𝑟
Şiddeti yeryüzeyinden dışa doğru azalıp, sonsuzda 0 ‘yaklaşmalıdır.
YERMANYETİK ALANIN KÜRESEL KOORDİNATLARDA GÖSTERİMİ
Yeryüzeyinde manyetik alanın yericinde bir dipolün meydana getirdiği
alan ile birlikte benzer olduğunu anlamak için küresel harmonik fonksiyon
analizini bilmemiz gerekir.
Maxwell denkleminden
x B=J +
𝜕𝐷
𝜕𝑡
(J=elektrik akım yoğunlupu;
𝜕𝐷
𝜕𝑡
= elektrik akım
yoğunluğu deplasmanı)
Yeryüzünden 50 km yüksekliğe olan bölge elektromanyetik boşluk olarak
kabul edilir. Bu bölgede J=0 ve
𝜕𝐷
𝜕𝑡
= 0’dır. Buradan x B=0 şeklini alır.
Rotasyonu 0 olan alan konservatif bir vektör alandır ve bu alanıın V
skaler gibi bir potansiyeli vardır.
Eğer x B=0 yani curl B=0 ise B=-grad V ; div B= .B=0
Div (-gradV)= 2 V=0 şeklinde V potansiyeli Laplace bağıntısını sağladığı
görülür.
Küresel koordinatlarda (r, ,) olmak üzere r yerkürenin merkezinden
olan radyal uzaklık, , co-latitüd açısı, ise boylam açısı olmak üzere
tanımlanır. Bunun sonucunda Laplace bağıntısını çözmemiz gerekir.
Laplace eşitliği
olup, Kartezyen koordinatlarda
Küresel koordinatlarda ise, r orijinden olan mesafe,
açısı, =boylam eğeridir.
co-latitude
Laplace eşitliğinin çözümleri harmonikler olarak adlandırılır.
Küresel koordinatlardaki çözümler ise küresel harmoniklerdir.
LaPlace Eşitliğinin Çözümü
Değişkenlerin
alalım. O zaman
Eşitlik
olarak ayrıldığını göz önüne
ile çarpılırsa,
Elde edilir.
Son terim sadece boylama bağlı olduğu için onu sabit kabul edip,
ilk iki terimi bu sabite eşit iki negatiflerin toplamı olarak göz önüne
alınır.
Bunu tekrar düzenlersek,
Yukarıdaki eşitlik
şeklinde göz önüne alınabilir.
Burada L() yerine x(t) konulmuş sabitler ise tekrar
isimlendirilmiştir. Bu harmonik osilatör problemleri için basit
diferansiyel eşitliği göstermektedir.
Bunun çözümü
şeklindedir.
, (m tamsayıdır)
Şimdi önceki iki terimi tekrar göz önüne alalım.
Eşitlik
ile çarpılırsa;
elde edilir.
Bu terimler bir önceki değişkende olduğu gibi bağımsız olmalı ve
bu yüzden her iki terim sabit olmalı. Bunu basit diferansiyel
eşitlikte;
şeklinde yazılır.
veya
Bunun çözümü;
( l tamsayı olup 0’a eşit veya büyüktür)
Sonuçta,
‘dir.
Bu ise diğer bir basit diferansiyel eşitlik olup, Legendre eşitliği
olarak ifade edilir. Çözümü
ise Legendre Polinomları olarak bilinir,
LaPlace eşitliğinin genel çözümü o zaman
şeklinde verilmektedir.
şeklindedir.
ise sabitlerdir.
Küresel harmonik analiz ile alanın kaynağının kürenin içinde mi yoksa
dışından mı kaynaklandığı belirlenir. Sadece belirli lokasyonlarda
yermanyetik alan bileşenleri elde edilmektedir. Eğer ölçüm değerleri
olmayan lokasyonlar varsa, o zaman eldeki tüm gözlemleri toplayarak
‘Global Yermanyeik Alan’ a ait bir model oluşturulur. Bu bize herhangi bir
yükseklik enlem ve boylam için alanın en iyi bulunabilen değerini
vermektedir.
Bunun
için
küresel
geometride
en
iyi
tanımlayabileceğimiz fonksiyonları bulmamız gerekmektedir.
periyodik fonksiyonlar elde edilir: Bir ‘T’ aralığındaki herhangi
şekilde
Örneğin
bir f(t)
fonksiyonu ‘m’ dalga sayısı ile sinuzoidlerin toplamı olarak gösterilebilir.
Laplace 2. Dereceden kısmi diferansiyel eşitliği Laplace’ın çözümü
harmonik fonksiyondur. V(x,y,z) potansiyelin türevi varsa ve sürekli ise
potansiyel harmoniktir ve Lplace denklemini gerçekleştirir.
Küresel Harmonik Analizin Sonuçları
Yermanyetik
alanın
küresel
harmonik
analizi
Laplace
eşitliğinin
sağlandığı ve belirli sınır şartlarında yer manyetik alanın konservatif
olduğu görülmüştür.
Yeryüzeyinin 420 km yüksekliğinde MAGSAT uydusundan elde edilen
jeomanyetik alan değerinin analizi sonucu
n=66’ya kadar Gauss katsayılarının değerleri hesaplanmıştır.
n>40 olan bölgeler belirsiz
n>50 olan bölgeler gürültü
15<n<40 terimleri kısa dalga boylu manyetik anomalileri göstermekte
(yerkabuğundaki mıknatıslanma ile ilgili)
n<14 terimleri sıvı dış çekirdekten kaynaklanan iç kaynaklı alanlardır.
Küresel harmonik analiz sonucu yerin potansiyel ifadesi iç kaynaklı ve
dış kaynaklı alandan oluştuğu görülmektedir.
𝑔𝑙𝑚 , 𝑞𝑙𝑚 = Gauss katsayılarıdır.
Yukarıdaki bağıntıda n 1 için açılırsa, bu açılımda Pnm cos
Bağımlı
Legendre
Fonksiyonu
P10 cos cos
ve
P11 cos sin
olduğundan,
a 3 g10
a 3 g11
a 3 h11
V 2 cos 2 cos sin 2 sin sin
r
r
r
Diğer taraftan küresel koordinat merkezinde, z, x ve y eksenlerine çakışık
mz , m x ve m y manyetik dipol momentlerin r uzaklıktaki bir P noktasında
V y potansiyelleri doğrultu cosinüsleri
meydana getirdikleri V z , V x ve
yardımıyla sırasıyla,
Vz
0 mz
cos
4r 2
Vx
0 mx
cos sin
4r 2
Vy
0 my
4r 2
sin sin
şeklinde elde edilir. V z , V x ve
V y potansiyellerinin uzaydaki dağılımları
sırasıyla cos / r 2 , cos sin / r 2 ve sin sin / r 2 ye bağlı mz , m x ve m y dipol
momentlerin Gauss katsayıları ile ilişkileri,
mz
4a 3
0
g10
şeklinde elde edilir.
mx
4a 3
0
g11
my
4a 3
0
h11
Yermanyetik alanın küresel harmonik analizinden elde edilen Gauss
katsayılarının ilk üçünün g10 , g11 , h11 değerleri, diğer katsayılardan oldukça
büyüktür (n = m = 10 açılımı için 120 katsatısı elde edilir). Dolayısıyla ilk
üç terimin dipol moment değerleri, diğer terimlerin ifade ettikleri dipol
moment değerlerinden büyüktür. Bu ilk üç dipole Jeosentrik Dipol adı
verilir. z eksenine, başka bir deyişle yerkürenin dönme eksenine çakışık
olduğu kabul edilen mz dipolü en büyük değere sahiptir. Bu dipole aksiyal
jeosentrik dipol (İngilizce axial geocentric dipole) denir. x eksenine
çakışık olduğu kabul edilen m x ve y eksenine çakışık olduğu kabul edilen
m y dipolleri ise ekvator düzleminde yer almaktadırlar. Bu üç jeosentrik
dipolün vektorel toplamları yerkürenin toplam jeosentrik dipol momentini
verir. Toplam jeosentrik dipol momentin büyüklüğü
m
4
0
3
a g
g h
0 2
1
1/ 2
1 2
1
1 2
1
bağıntısı ve doğrultusu da,
tan g11
h / g
2
1 2
1
0
1
ve
tan h11 / g11
bağıntıları ile bulunur.
Şekil P noktasının küresel koordinatları ile merkezde x, y ve z
eksenlerine çakışık olduğu kabul edilen mx, my ve mz manyetik dipol
momentleri.
Toplam jeosentrik dipol momentin ekseni, günümüzde yerkürenin dönme
ekseni ile 9.98o’ lik bir açı yapar. Bu toplam (eğimli) jeosentrik dipol
ekseninin yeryüzünü kestiği noktalara
jeomanyetik kutup adı verilir.
2010 yılı verilerine göre kuzey jeomanyetik kutup 80,02o K, 71,98o B ve
güney jeomanyetik kutup ise 80,02o G, 108,02o D noktalarında yer alırlar.
Bu kutup noktaları yeryüzünde tam karşılıklı olarak bulunurlar.
Jeomanyetik kutuplar dışında Yerküre ayrıca, eğim açısının 90o veya
yatay bileşenin sıfır olduğu noktalarda manyetik kutuplar veya eğim
kutupları adı verilen kutuplara sahiptir. Bu kutuplar dipol alanı ile birlikte
dipol olmayan ve anomali alanlarını da içeren gerçek kutuplardır. Başka
bir deyişle manyetik pusulanın gösterdiği kutuplardır. 2010 yılında kuzey
manyetik kutup 85,19o K, 133,16o B ve güney manyetik kutup 64,44o G,
137,44o D noktalarında yer almaktadır. Bu kutuplar yeryüzünde karşılıklı
olarak bulunmazlar.
Dipol Alan
Yeryüzeyince yer manyetik alanının en önemli bölümü dipol alandır. Bu
alan n=1 gauss katsayıları ile verilmektedir. Yerin potansiyel ifadesinde
ilk terimleri yazarsak
V=
𝑅 3 𝑔10 𝑐𝑜𝑠𝜃
m=
𝑟2
4𝜋
𝜇0
𝑅 3 𝑔10
𝑔10 = alanın en güçlü bileşenidir. Bu terim yerin dönme ekseni ile çakışık
yerin merkezindeki dipolü tanımlar. Buna jeosentrik aksiyal manyetik
dipol denilmekteydi.
Dipolün manyetik alanı (B) dipol ekseni etrafında simetriktir. Dipol ile r
uzaklıkta açısı yapan herhangi bir R uzaklığında dipolün radyal ve
tanjantiyal bileşenleri potansiyeli r ve göre türevlerinin alınmasıyla elde
edilir.
Br =
B =
−𝜕𝑣
𝜕𝑟
=
−1 𝜕𝑣
𝑟 𝜕Ѳ
𝜇 0 2𝑚𝑐𝑜𝑠𝜃
4𝜋
=
𝑟3
𝜇 0 𝑚𝑐𝑜𝑠𝜃
4𝜋
𝑟3
düşey bileşen. (Düşey bileşen V =
yatay bileşen. (Yatay bileşen H =
2𝑚𝑠𝑖𝑛𝜃
𝑅3
𝑚𝑠𝑖𝑛𝜃
𝑅3
)
)
Düşey bileşen ekvatorda kaybolur. = 90 alan yataydır.
B yatay alan bileşeninin B = 𝑔10 ‘e eşit olduğu bulunur. (r, ) gibi bir
noktada manyetik kuvvet çizgileri I açısıyla yüzeye eğimlidir. Bu da;
=
𝐵𝑟
𝐵𝜃
= 2 tg λ = 2 cot (I=eğim açısı, = kutup açısıdır).
tgI
𝑔1′ ve ℎ1′ - diğer yüksek potansiyel bileşenleri ifade etmektedir.
bileşenler
ekseni ekvator
yüzeyinde
olan
dipollerin
Bu
potansiyelini
tanımlamaktadır. Böylece yerkürenin toplam dipol momenti:
m=
4𝜋
𝜇
R3
(𝑔10 )² + (𝑔1′ )² + (ℎ1′ )²
Yermanyetik alanının 2005 yılında yapılan analizi sonucu aşağıdaki dipol
bileşenleri elde edilmiştir.
𝑔10 = - 295568 nT, 𝑔1′ = -16718 nT, ℎ1′ = 5080 nT
Bu katsayıları kullanarak elde edilen dipol moment: m = 7. 7674 x 10 ²²
Am²’ dir.
Yerkürenin manyetik kutupları manyetik alana eğim açısının 90o olduğu
yerlerdir. 1980 yılı için elde edilen izoklin haritası (sabit eğim açısı
değerlerini göstermektedir) kuzey manyetik kutbun 77.3oK, 258.2oD da
güney manyetik kutbun ise 65.6oK, 139.4oD enlem ve boylamlarında
olduğunu göstermektedir (Şekil a).
Kutuplar tam olarak birbirinin zıt yönünde bulunmamaktadır. Manyetik
kutuplar ve jeomanyetik kutuplar sırasıyla pusulanın gösterdiği enlem,
boylam ve jeomanyetik analiz sonucu elde edilen enlem,boylama karşılık
gelmektedir. Bu fark yer manyetik alanının tam bir mükemmel dipolu
temsil etmemesinden dolayıdır. Yermanyetik alanını şiddeti ekvatorlar
karşılaştırdığımızda yüksek enlemlerde daha büyüktür (Şekil b). Güney
Atlantikdeki manyetik alan şiddeti beklenenden 20 mikroT daha düşüktür.
Yermanyetik
alanı
yerin
kozmik
radyasyonlardan
ve
güneş
rüzgarlarından koruduğu için, bu kalkan görevi Güney Atlantik’de daha
azdır.
Yermanyetik alanını şiddeti ekvatorlar karşılaştırdığımızda yüksek
enlemlerde daha büyüktür (Şekil b). Güney Atlantikdeki manyetik alan
şiddeti beklenenden 20 mikroT daha düşüktür. Yermanyetik alanı yerin
kozmik radyasyonlardan ve güneş rüzgarlarından koruduğu için, bu
kalkan görevi Güney Atlantik’de daha azdır.
Dipol Olmayan Alan
Eğimli jeosentrik dipol alanını toplam alandan çıkarılmasıyla elde edilir.
Dipol olmayan alan alanın yüksek dalga boylu manyetik anomalilere
sebep olmaktadır (Şekil). Bu alanı tanımlamak için n ≥ 2 sırasındaki tüm
terimlerin potansiyel açılımı kullanılmaktadır.
Seküler Değişim
Yerin herhangi bir noktasında jeomanyetik alan zamana göre sabit
değildir. Yerin iç kaynaklı alanına ait Gauss katsayıları bir dönemden
diğerine göre karşılaştırıldıklarında bu değerlerde yavaş ama önemli
değişiklikler elde edilmiştir. Zamana göre alandaki bu değişimlere seküler
değişim denilmektedir. Bu değişimler hem dipol hem dipol olmayan
alanda görülmektedir.
Dipol Alanda Seküler Değişim
Dipol alandaki seküler değişim hem şiddet hem de doğrultuda
görülmektedir. Farklı dönemlerde Gauss katsayılarının hesaplanması
sonucu 1550 – 1900 yılları arası her bir yüzyıl için dipol moment
kuvvetinde % 3.2 lik lineer bir düşüş görülmektedir. Son 80 yılda bu
düşüş % 5.8 olarak saptanmıştır. Eğer bu düşüş aynı oranda devam
ederse alanın şiddeti 2000 yıl sonra 0 olacaktır (Şekil). Şiddetteki bu
hızlı düşüşün nedeni bilinmemekle birlikte bir sonraki ters dönmeye
işaret edebilmektedir. Bir diğer yoruma göre dipol momentindeki bu
düşüş yeni bir terslenmenin göstergesidir.
Dipol ekseninin yeri de seküler değişim göstermektedir. Eğer dipol eksen
ve yerin dönme ekseni arasındaki açıyı zamana göre grafiklediğimizde
bu değişim görülebilmektedir. 16. YY’daki veriler dipol ekseninin rotasyon
eksenine göre 3o eğimli olduğu ve 16-19 YY’lar arasında azar azar bir
artışın olduğunu göstermektedir. Dipol eksenin son 200 yılda rotasyon
eksenine göre 11-12o’ lik sabit bir tiltlenmeye sahip olduğu görülmüştür.
Son 400 yılda jeomanyetik alanın boylamı sabit şekilde batıya doğru
çekilmektedir. 19. YY’ dan önce kutup 0.14o/yıl ile batıya kayarken, 19.
YY da kutbun batıya kayması azalmış ve bu oran 0.044o/yıl olarak
saptanmıştır.