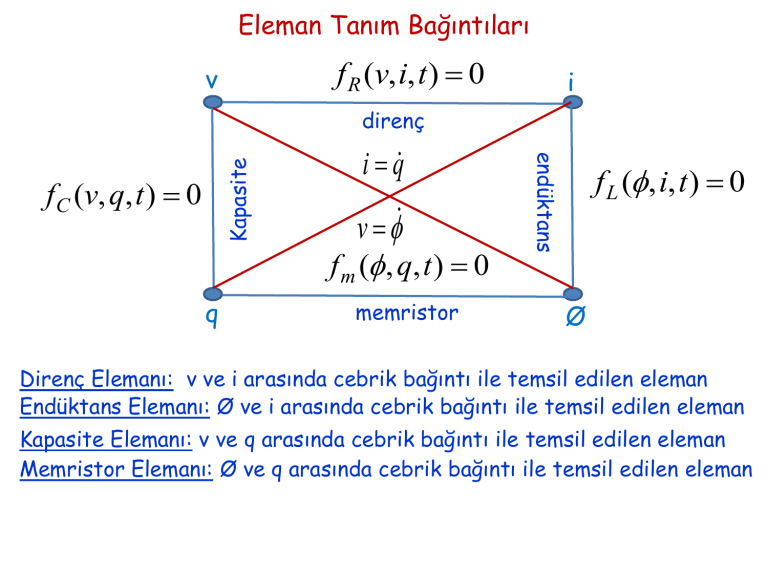
Eleman Tanım Bağıntıları
f R (v, i, t ) 0
v
i
fC (v, q, t ) 0
q
i q
v
f m ( , q, t ) 0
memristor
endüktans
Kapasite
direnç
f L ( , i, t ) 0
Ø
Direnç Elemanı: v ve i arasında cebrik bağıntı ile temsil edilen eleman
Endüktans Elemanı: Ø ve i arasında cebrik bağıntı ile temsil edilen eleman
Kapasite Elemanı: v ve q arasında cebrik bağıntı ile temsil edilen eleman
Memristor Elemanı: Ø ve q arasında cebrik bağıntı ile temsil edilen eleman
2-Uçlu Direnç Elemanları
• lineer, lineer olmayan, zamanla değişen, değişmeyen, akım
ve/veya gerilim kontrollü dirençlerin tanım bağıntıları,
• seri, parallel bağlı dirençlere ilişkin uç bağıntıları,
• lineer olmayan dirençlere ilişkin dc (doğru akım) çalışma
noktasının belirlenmesi, küçük işaret analizi.
Lineer Direnç
+
()
v(t ) Ri (t )
direnç
i (t ) Gv(t )
iletkenlik, siemens
mho
v
v (t )
(S )
i (t )
v (t )
i (t )
i-v düzlemi
v-i düzlemi
Hatırlatma: Lineerlik
f ( x1 ) y1
f ( x2 ) y2
f (.) lineer
f (x1 x2 ) f ( x1 ) f ( x2 )
y1 y 2
Özel Lineer Dirençler:
Açık devre elemanı
f (i, v) i 0
v (t )
i (t )
R
G0
i (t )
i-v düzlemi
v (t )
v-i düzlemi
Kısa devre elemanı
f (i, v) v 0
v (t )
R0
i (t )
G
v (t )
i (t )
i-v düzlemi
v-i düzlemi
Açık devre elemanı ve kısa devre elemanının i-v,v-i karakteristiklerine
dikkat edelim !!!
v (t )
i (t )
R
G0
i (t )
i-v düzlemi
v (t )
v-i düzlemi
Tanım: (Dual Dirençler)
A direncinin v-i karakteristiği B direncinin i-v karakteristiği ile aynıdır.
A direnci B direncinin dual’idir.
Lineer direnç elemanına ilişkin ani güç
Lineer Olmayan Direnç
+
v
_
f ( v, i ) 0
p(t ) v(t )i (t ) Ri 2 (t )
Bazı Özel Lineer Olmayan Dirençler
İdeal Diyot
+
v
_
RID {( v, i) : vi 0, i 0, v 0 ve v 0, i 0}
Diyot tıkamada
Diyot iletimde
(v 0),
(i 0),
i0
v0
v (t )
i (t )
i (t )
v (t )
i(t )
i-v düzlemi
v-i düzlemi
Diyot tıkamada iken davranışı hangi eleman gibi?
Is
v(t )
Diyot iletimde iken davranışı hangi eleman gibi?
p-n Jonksiyon Diyodu (alçak frekanslardaki özellikleri)
+
v
_
uç büyüklükleri
v
RD {( v, i ) : i I s [exp( ) 1], I s , vT sabit }
vT
q elektron yükü
kT
I s ters doyma akımı VT
k Boltzman sabiti
q
T Sıcaklık (Kelvin)
VT 0,026V
Tünel Diyod
+
RTD {( v, i ) : i iˆ(v)}
v
i (t )
İ1
v1 v v2 eğim negatif
_
osilatör, kuvvetlendirici
İ2
İ 2 i İ1 her akıma
üç gerilim karşılık düşüyor
hafıza, anahtarlama
V1 V2
gerilim kontrollü, akım kontrollü değil
Bağımsız kaynaklar
Bağımsız gerilim kaynağı
+
+
vs (t ) vs (t )
_
_
v(t )
Rvs {( v, i) : v vs (t ), i }
i (t )
v (t )
Bağımsız gerilim kaynağı lineer eleman mı?
Bağımsız gerilim kaynağı gerilim kontrollü mü?
Bağımsız gerilim kaynağı akım kontrollü mü?
vs (t ) 3V
Bağımsız akım kaynağı
+
is (t )
v
Ris {( v, i) : i is (t ), v }
_
Zamanla Değişen Dirençler
v-i karakteristiği zamanla değişen dirence zamanla değişen direnç denir.
Lineer Zamanla Değişen Direnç
+
v
v(t ) R(t )i (t )
v (t )
R (t )
i (t ) G (t )v(t )
i (t )
_
t
