ENM 319 KALİTE KONTROL
Yrd. Doç. Dr. Ercan ŞENYİĞİT
Bu ders notunun hazırlanmasında Montgomery’in Statistical Quality Control kitabı kaynak olarak
kullanılmıştır.
Kalite
• Kalite, bir ürün veya hizmetin belirlenen veya
olabilecek ihtiyaçları karşılamaya dayalı
karakteristikler toplamıdır. (ISO)
• Kalite: Müşteri beklentilerini uygun bir
biçimde karşılayacak ürün veya hizmet
üretebilme yeteneğidir.
• KALİTE DEĞİŞKENLİKLE TERS ORANTILIDIR.
DEĞİŞKENLİK
• Herhangi bir süreçte, kontrolümüzde olmayan
değişkenliğin nedenleri vardır.
• Fazla değişkenlik, ürün hatalarına, mutsuz
müşterilere ve gereksiz maliyetlere neden olur.
• Değişkenliği anlamada ve iyileştirmeyi
sağlamada yardımcı olmak üzere değişkenliği
belirlemek ve niceleştirmek için istatistiksel
yöntemler kullanılabilir.
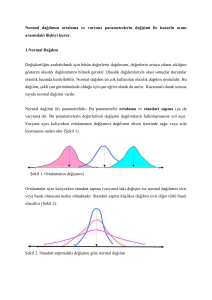
Vites Kutusu örneği
Ford firmasının 1980’lerdeki bir deneyimi, parça üretiminde hedeften
sapma sonucu oluşan varyasyonun, firmaya parasal kayıp olarak
döndüğünü göstermektedir. Ford, imal etmekte olduğu otolara
şanzıman üretmek üzere iki ayrı firmaya sipariş verir. Tedarikçi
firmalardan biri, bir Amerikan firması, diğeri Japon Mazda firmasıdır.
Her iki firma da, şanzımanları, Ford’un spesifikasyonlarına göre üretip
teslim ederler. Garanti süresi içinde şanzıman sorunlarından
kaynaklanan garanti talepleri oluşur. Ford yetkilileri, sorunlu
şanzımanları üretici firmaya göre sınıflandırdıklarında, Amerikan
firmasının ürettiği grubun, sayısal olarak diğerinden birkaç kat daha
fazla olduğunu görürler. Bunun üzerine, şanzımanların bazı kritik
performans değişkenlerinin olasılık dağılımını hesaplarlar. Durum
Şekillerdeki gibidir. Her iki firmanın da ürettiği şanzımanlar, istenilen
spesifikasyon sınırları içerisindedir. Ancak, Amerikan firmasının ürettiği
şanzımanlarda değişkenlik daha fazladır. Bu şanzımanlar, daha sık ve
daha erken arıza yaparak firmanın maliyetini artırmaktadır.
Kalitenin iyileştirilmesi
• Kalite iyileştirmesi, süreçlerde ve ürünlerde
değişkenliği azaltmaktır.
• Vites kutusu örneği, bu tanımın anlamını
açıklamaktadır.
• Eşdeğer bir tanıma göre, kalite iyileştirmesi
israfın azaltılmasıdır. Bu tanım, hizmetlerde
veya işlemlere dayalı işler için yararlıdır.
Ürün kalite boyutları
• Performans; temel işletim özellikleri, (resmin parlaklığı)
• Özellikler; temel özelliklere ek olarak eklenen özellikler (uzaktan
kumanda)
• Güvenilirlik; zaman içinde ürünün bozulma olasılığı
• Uygunluk; belirlenmiş standartlara uygunluk
• Dayanıklılık; yenilemeden önceki yaşam süresi
• Servis görebilirlik; onarımın kolay olması, hızı ve onarımın yetkinliği
• Estetik; görünüm, hissedilmesi, ses, koku ve tat
• Güvenlik; Kaza ve zarar olmaması
• Diğer algılamalar; marka, reklam, vb. etmenlere dayalı niteliksel
algılamalar
Hizmet kalite boyutları
• Zaman ve zamanlılık; müşterinin bekleme zamanını
en aza indirme , işi zamanında tamamlama
• Bütünlük; müşterinin istediklerinin tümünün
almasının sağlanması
• Nezaket; müşteriye davranışın uygunluğu
• İstikrar; tüm müşteriler için aynı düzeyde hizmet
• Erişebilirlik ve kolaylık; hizmeti almanın kolaylığı
• Doğruluk; işi her zaman doğru yapabilme
• Heveslilik; olağandışı durumlara yanıt verebilme
Örnekler
Boyut
Ürün
Otomobil
Hizmet
Otomobil Tamiri
Performans
Her özelliğin çalışması
Sabit fiyat, nezaket
Estetik
Kontrol panelinin görünümü
Temiz salon, çay ikramı
Özel nitelikler
(uygunluk, ileri teknoloji)
CD çalar, arka görüş kamerası
olması
Hızlı geri dönüş
Güvenlik
Hava yastığı olması
Kırılmaz camla ayrılmış bekleme
salonu
Güvenilirlik
Arızaların az olması
Zamanında doğru işin yapılması
Dayanıklılık
Kullanım ömrünün uzun olması
Daha uzun süre dayanması
Algılanan Kalite
Lüks
Ödül kazanma
Satış sonrası Hizmet
Şikayetleri zamanında ortadan
kaldırma
Şikayetlerle ilgilenme
4 unsur kaliteyi belirler.
• Tasarım kalitesi: İstenen ürün veya hizmet
özelliklerinin tasarımda bulunması
• Uygunluk kalitesi: Geliştirilen ürün veya
hizmetin tasarıma uygun olması
• Ürün:
• Hizmet: Müşteri beklentilerinin üzerine
çıkabilme
Yetersiz kalite
•
•
•
•
•
•
İşi ve müşteriyi kaybetmeye;
Ödemelerin gecikmesine
Verimliliğin düşmesine
Maliyetlerin artmasına yol açabilir.
Kalite tüm çalışanların sorumluğundadır
Özellikle üst yönetimin sorumluğundadır.
Kalite’nin Anlamı
Kalite
Üretici Bakışı
Üretim
Kullanıcı Bakışı
Tasarım Kalitesi
• Kalite
Uygunluk Kalitesi
• Spesifikasyonlara
Uygunluk
• Maliyet
Karakteristikleri
• Fiyat
Müşteri
Kullanımına
Uygunluk
Pazarlama
Kalite Mühendisliği
• Kalite
mühendisliği,
ürünün
kalite
karakteristiklerini nominal veya istenilen
düzeyde tutmak amacıyla kuruluşun işlemsel,
yönetsel ve mühendislik faaliyetleri kümesidir.
Kaliteyi etkileyen faktörler
İkiye ayrılır.
• Firma içi faktörler
• Firma dışı faktörler
•
•
•
•
Kalitenin boyutları
Tasarım kalitesi
Uygunluk kalitesi
Performans kalitesi
Firma içi faktörler
•
•
•
•
•
•
•
Yönetim
İnsan gücü
Çalışanların motivasyonu
Malzeme
Makine
Üretim yöntemleri
Ölçüm araç ve gereçleri
Firma dışı faktörler
•
•
•
•
Tüketici özellikleri
Pazarın yapısı
Sermaye ve finansal kaynaklar
Teknoloji
Bilim Adamları
• Shewart, Kontrol grafiklerini geliştirdi.
• Deming, Toplam kalite yönetiminin kurucusu
olarak kabul edilmektedir. Kalitenin bir
yönetim sistemi olduğunu ifade eden Deming
kurallarını geliştirmiştir (14 kural).
• Feigenbaum, toplam kalite kontrolu kavramını
geliştirmiştir. Feigenbaum’un üçgen modeli
bulunmaktadır.
Deming döngüsü
PÜKO DÖNGÜSÜ
Planla
Uygula
Önlem al
Kontrol et
Bilim Adamları
• Juran, spiral modeli geliştirmiştir.
• Crosby, sıfır hata kavramının öncülerindendir.
• İshikawa, kalite çemberlerini geliştirmiştir.
Balık-kılçığı yöntemini de geliştirmiştir.
• Taguchi, deneysel tasarım ve kalite kayıp
fonksiyonunu geliştirmiştir.
• Ohna, tam zamanında üretim JIT modelini
geliştirmiştir.
Bilim Adamları
• İmai, sürekli gelişme- kaizen kavramını
geliştirmiştir.
• Shingo, sıfır hata kavramını incelemiş ve pokayoke kavramını literatüre kazandırmıştır.
• Juran, kalite üçlemesini geliştirdi. Bunlar,
planlama, kontrol, iyileştirmedir.
TEMEL KAVRAMLAR
• Proses: Herhangi bir ürün veya hizmetin
müşteri
isteklerini
karşılayacak
kalite
düzeyinde elde edilebilmesi için gerekli
faaliyetler ile makine, alet/ekipman, yöntem,
malzeme ve işgücü gibi faktörlerin sistematik
bir şekilde planladığı sistemin tümüne denir.
TEMEL KAVRAMLAR
• İstatistiksel kalite kontrol, en az maliyetle,
zamanında ve doğru veri üretmektir.
• Örneklem dışı hata büyüklüklerinin kontrolüne
yardımcı olan istatistiksel kalite kontrol
yöntemleri
1. İstatistiksel proses kontrol
2. Ürün kontrol
İstatistiksel proses kontrol
İstatistiksel tekniklerin, bir üretim veya hizmet
prosesinin olağan biçimde devam edip
etmediğinin istatistiksel tekniklerle kontrolü,
olağandışı bir durum varsa bunun fark edilmesi
ve nedenlerinin belirlenerek ortadan kaldırılması
olarak ifade edilebilir.
İstatistiksel kalite kontrol
İstatistiksel proses kontrolünü, örnekleme
planlarını ve diğer istatistiksel teknikleri ve
uygulamalarını içerir ve kalitenin sürekli olarak
izlenmesine ve gerektiğinde önlem alınmasına
dayanan bir yöntemdir.
Muayene ve Kalite Kontrol
• Herhangi bir ürünün veya hizmetin ölçü,
nitelik
veya
performansının
önceden
belirlenmiş
spesifikasyonlara
uyup
uymadığının belirlenmesi işlemine muayene
denir.
• Muayene kalite kontrolün bir fonksiyonudur.
• Muayene işleminde geçmiş üretimin kalitesi
üzerinde durulmakta iken, kalite kontrolünde
gelecek üretime önem verilmektedir.
Nicel ve Nitel Değişken
• Birimin sahip olduğu ve bir diğerinden ayırt
edilmesine yarayan özelliğe değişken denir.
• Şıkları kelimelerle ifade edilebilen değişkenlere
nitel değişkenler, sayılarla ifade edilebilen
değişkenlere ise nicel değişkenler denir.
Kalite güvence sistemi
Toplam Kalite Kontrol anlayışı çerçevesinde
kalite kontrol fonksiyonun etkin bir şekilde
gerçekleştirilebilmesine ilişkin bilgiler sağlayan
bir faaliyetler sistemidir.
Kalitenin birincil boyutları
•
•
•
•
•
•
•
•
Performans
Tamamlayıcı özellikler
Uygunluk
Güvenirlik
Dayanıklılık
Hizmet görme yeteneği
Estetik
İmaj
Kalitenin ikincil boyutları:
•
•
•
•
Fiyat
İnsan sağlığı ve güvenliği
Kolay bulunabilirlik
Kullanım kolaylığı
Değişkenlik
• Bir prosesten elde edilen ürünler, aynı yöntem
ve makinelerin kullanımına rağmen kalite
özellikleri birbirinin tıpa tıp aynı olmayıp her
zaman birbirinden az da olsa farklılık
gösterebilir.
• Değişkenliğin iki ana nedeni vardır.
1. Genel nedenler
2. Özel nedenler
Prosesteki değişkenlik
• Prosesteki değişkenliğin hangi tür değişkenlik
olduğunun belirlenmesi üretici için son derece
önemlidir. Ancak, bu belirleme aşamasında iki
tip hata ile karşılaşılması muhtemeldir. Bunlar;
• Özel neden yokken aranıp üretim işleminde
düzeltmeye gidilmesi (1. tip hata)
• Özel neden varken aranmaması veya ortadan
kaldırılmaması (2. tip hata)
Type 1 error is % 0.27
-3σ -2 σ
Ort.
%99.73
+2 σ +3σ
Standartlar
Bir ürünün kalite özellikleriyle ilgili ürün tasarımı,
üretim, ölçme vb. konularda karışıklıktan
kurtulmak ve belirli bir düzen kurmak amacıyla
önceden belirlenmiş kurallara denir.
Spesifikasyon ve Toleranslar
• Spesifikasyonlar, standartlara göre dar
kapsamlı olup, standartların uygulanmasına
yardımcı olan özelliklerdir. Spesifikasyonlar,
standartlaştırmada kullanılan araçlardır.
• Örneğin, bir milin nominal çapı ve izin verilen
sapmalar
için
belirlenen
rakamlar
spesifikasyonları, bu rakamların belirlenme
biçimi veya belirli kurallara uygunluğu ise
standardı oluşturur.
Spesifikasyon ve Toleranslar
• Ürün tasarımında öngörülerek belirli sınırlar
içinde olması beklenen ve sadece bu sınırlar
içinde gerçekleştiği zaman kabul edilebilen
sapmalara tolerans denir.
• Ürün kalitesinin kabul edilebilir alt ve üst
sınırlarına spesifikasyon sınırları denir.
Kontrol sınırları
• Kontrol sınırları ile spesifikasyon sınırları aynı
değildir. Spesifikasyon sınırları, ürünün kabul
edilebilir sınırlarını ifade eder ve ürün
kalitesinin belirlenmesinde kullanılan bir ölçü
olarak düşünülebilir. Kontrol sınırları ise
prosesin kontrol altında olup olmadığının
belirlenmesi için çizilen ve proses ortalaması
ile proses değişkenliğine bağlı güven
sınırlarıdır.
Kalite Maliyetleri
• Toplam kalite yönetimini, felsefe veya anlayış
olarak kabul eden firmalar için, kaliteli ürünün
en düşük maliyetle üretilmesi temel amaçtır.
• İlk seferinde doğru yap ilkesi ile maliyetler en
aza iner.
Kalite Maliyetleri
• İyi kaliteyi sağlamanın maliyeti
- Önleme Maliyetleri
- Değerlendirme Maliyetleri
• Başarısızlık Maliyeti
- İçsel başarısızlık maliyetleri
- Dışsal başarısızlık maliyetleri
Önleme Maliyetleri
• Önleme maliyetleri, uygunsuzluğu önlemek için oluşan
maliyetleri içerir.
• Bunlar, genellikle,ürünün ilk seferde doğru olarak yapımı
için gerekli gayretler ile ilgili maliyetleri içerir.
• Önleme maliyetlerinin önemli alt grupları şunlardır:
- Kalite planlama ve mühendislik
- Yeni ürünlerin gözden geçirilmesi
- Ürün ve süreç tasarımı
- Süreç kontrol
- Eğitim
- Kalite verilerinin toplanması ve analizi
Değerlendirme Maliyetleri
•
•
•
•
Muayene ve giren malzemenin testi
Ürün muayene ve testi
Tüketilen malzemeler ve hizmetler
Test donatımlarının doğruluklarının
sağlanması ve bakımı
İçsel Hata Maliyetleri
• İçsel hata maliyetleri, ürünlerin, bileşenlerin
(components), malzemelerin ve hizmetlerin
kalite ihtiyaçlarını karşılamadığı zaman
oluşurlar
• Bu hata, ürün müşteriye teslim edilmeden
önce keşfedilir
• İçsel hata maliyetleri, üründe kusurların
bulunmaması halinde yok olurlar.
İçsel Hata Maliyetleri (Devam)
Bu maliyetlerin alt kategorileri şunlardır:
• Hurda
• Yeniden işleme
• Yeniden test etme
• Hata analizi
• Aksaklık (down-time) süresi
• Getiri kayıpları
• Değer düşüklüğü
Dışsal Hata Maliyetleri
• Dışsal hata maliyetleri, ürünün müşteriye
gönderildikten sonra, tatminkar düzeyde
işlevini yerine getirmediği durumda oluşur
• Bu maliyetler, ürünün her birimi ihtiyaçlarına
veya belirtimlerine (spesifikasyonlarına) uygun
hale getirildiğinde yok olurlar
Dışsal Hata Maliyetleri (Devam)
Temel alt kategorileri şunlardır:
• Şikayetlerin giderilmesi
• Geri gönderilen ürün/malzeme
• Garanti belgesi masrafları
• Yükümlülük maliyetleri
• Dolaylı maliyetler
Kalite Endeksleri
• İşçilik Endeksi:
kalite Maliyeti / işgücü saati
• Maliyet Endeksi:
kalite maliyeti / imalat maliyeti
• Satışlar Endeksi:
kalite maliyeti / satışlar
• Üretim Endeksi:
kalite maliyeti / üretilen birimler
Kalite Endeks Örneği
Kalite maliyetleri
Önleme
Değerlendirmel
İçsel hata
Dışsal hata
Toplam
Muhasebe ölçümleri
Satışlar
İmalat maliyetleri
1996
1997
1998
1999
$ 27,000
155,000
386,400
242,000
$ 810,400
41,500
122,500
469,200
196,000
829,200
74,600
113,400
347,800
103,500
639,300
112,300
107,000
219,100
106,000
544,400
$ 4,360,000
1,760,000
4,450,000
1,810,000
5,050,000
1,880,000
5,190,000
1,890,000
Kalite Endeksi
Toplam kalite maliyetleri * 100 / baz
$810,400 * 100 / 4,360,000 = 18.58
Yıl
1996
1997
1998
1999
Satışlar
18.58
18.63
12.66
10.49
Maliyet
46.04
45.18
34.00
28.80
Kalite ve Verimlilik
• Verimlilik= Çıktı / Girdi
• Az sayıda kusurlular, çıktıyı arttırır
• Kalite iyileştirme, girdileri azaltır
Getiri ve Verimliliğin Ölçümü
Y = (I)(%G) + (I)(1-%G)(%R)
Y = getiri
I = üretime başlıyan birimlerin sayısı
% G = kusursuz birimlerin yüzdesi
% R = yeniden işlenen kusurlu birimlerin yüzdesi
Ürün Getiri Örneği”
Günde 100 motorla üretime başla
Birimlerin 80%’i kusursuz
Düşük kalitedeki birimlerin 50%’si yeniden
işlenebilmektedir
Y = (I)(%G) + (I)(1-%G)(%R)
Y = 100 (0.80) + 100 (1- 0.80) (0.50) = 90 motors
Ürün Maliyeti
direct mfg costinput unit rework costreworked units
=
yield
K dI K r R
=
Y
where
K
d
direct manufacturing cost
Kr rework cost per unit
Y yield
I = input
R reworked units
Ürün Maliyet Örneği
Dolaysız imalat maliyeti = $30, yeniden işleme maliyeti = $12
100, üretime başlayan motor sayısı, 20%, kusurlu motor yüzdesi
Kusurlu motorların 50%’si yeniden işlenebilir
I K R
K
Ürün maliyeti =
d
r
Y
$30100 $1210 $34.67
=
90 motor
Çok Aşamalı Ürün Getirisi
Y = (I) (%g1)(%g2)...(%gn)
I = giren parti büyüklüğü
%gi = aşama i deki kusursuz
ürünlerin yüzdesi
Çok Aşamalı Süreç Getiri Örneği
Motorlar 4 aşamalı süreçte üretilmektedir.
Üretime 100 motorla başlandığında sürecin getirisini
hesaplayınız.
Aşama
Kusursuz ürün yüzdesi
1
0.93
2
0.95
3
0.97
4
0.92
Y = (I) (%g1)(%g2)...(%gn) = (100)(0.93)(0.95)(0.97)(0.92)
Y = 78.8 motor
100 Kusursuz Ürün Üretimi Çıktısı için
Gerekli Girdi Sayısı
Y
I=
%g1 %g 2 %g 3 %g 4
100
I=
0.930.950.97 0.92
126.8 motor
Kalite Verimlilik Oranı (KVO)
• Verimlilik ve kalite maliyetlerini içerir
• Artar
- Eğer işleme veya yeniden işleme
maliyetleri azalırsa
- Eğer süreç getirisi artarsa
QPR
İyi kalitedeki ürünler
(100)
(girdiler) (üretim maliyeti) + (kusurlu ürünler)(yeniden işşlem maliyeti)
KVO Örneği
Dolaysız maliyet = $30/birim, yeniden işleme = $12/birim
Günde 100 motorla üretime başla
Ürünlerin %80’i kusursuz, kusurlu birimlerin %50’si yeniden
işlenebilir olduğunda kuruluş aşağıdaki 4 değişiklik üzerinde
çalışmaktadır
1 - Günlük üretimin 200’e çıkarılması
2 - Süreç maliyetinin $26’a ve yeniden işleme
maliyetinin de $10’a indirilmesi
3 - Getirinin 95%’e çıkarılması
4 - 2 ve 3. ün karışımı
KVO ÖRNEĞİ
80 10
QPR
(100) 2.88
(100)($30) + (10)($12)
• Durum 1 – I’yı artırmanın bir etkisi olmadı
160 20
QPR
(100) 2.88
(200)($30) + (20)($12)
• Durum 2 – Maliyetin azaltılması QPR’ı artırdı
QPR
80 10
(100) 3.33
(100)($26) + (10)($10)
• Durum 3 – Getirinin artması QPR’ı artırdı
QPR
95 2.5
(100) 3.21
(100)($30) + (2.5)($12)
• Durum 4 – Maliyetlerin düşmesi ve getirinin
artması en iyi durumu verdi
95 2.5
QPR
(100) 3.71
(100)($26) + (2.5)($10)
İstatistiksel Kalite Kontrol Teknikleri
İstatistiksel Proses (Süreç) Kontrol
• İstatistiksel Süreç Kontrol bir araçlar topluluğu
olup birlikte kullanıldığında değişkenliği azaltır
ve süreci kararlı kılar.
• İstatistiksel Süreç Kontrolün nihai amacı,
nedeni bulunabilir sorunların tanımlanmasıyla
süreçlerdeki değişkenliğin elimine edilmesi
veya azaltılmasıdır.
İstatistiksel Proses (Süreç) Kontrol
• İstatistiksel Süreç Kontrolün en önemli amacı,
nedeni bulunabilir sorunların tanımlanmasıyla
veya prosesteki değişimin özel nedenlerini
ortadan kaldırılması, süreçlerdeki değişkenliğin
elimine edilmesi veya azaltılmasıdır.
• Herhangi bir proses, sadece genel nedenlerin
etkisiyle değişim gösteriyorsa , bu prosesin
istatistiksel olarak kontrol altında çalıştığı
söylenir.
Kontrol Grafikleri
• Kontrol grafikleri, proseslerden elde edilen
ürünlerin gözlem sonuçlarına ilişkin değişimleri
ortaya koyar.
• Kontrol grafikleri görsel bir nitelik taşır ve
prosesteki değişkenliğin kolayca algılanmasına
yardımcı olur.
• Prosesleri kontrol altına almak, oluşacak kusurları
zamanında ve ortaya çıkmadan önce önlemek,
prosesleri iyileştirmek ve geliştirmek amacıyla
kontrol grafikleri kullanılır.
Kontrol Şemalarının İstatistiksel Yapısı
Örnek Kalite Özelliği
Üst Kontrol Sınırı
Merkez çizgisi
Alt Kontrol Sınırı
Örnek Sayısı veya Zamanı
Tipik Bir Kontrol Şeması
Kontrol Grafikleri
Kontrol grafikleri, üretimden belirli ve eşit zaman aralıklarında
alınan örneklerden elde edilen ölçüm değerlerinin zaman
içerisindeki değişimlerinin gösterildiği grafiklerdir.
• Merkez Çizgi; kalite
özelliğinin ortalama değeri
(hedeflenen değer)
• Üst Kontrol Sınırı
• Alt Kontrol Sınırı
Kontrol Grafikleri
• Merkez çizgi, çeşitli zaman aralıklarında
prosesten alınan ürünlere ilişkin gözlem
değerlerinin ortalamasını gösteren çizgidir.
• Üst ve alt kontrol sınırları, prosesten alınan
ürünlere ilişkin gözlem değerlerinden
hareketle hesaplanan ve orta çizgiye eşit
uzaklıkta olan (±3σ) olan sınırlardır.
Normal Dağılım
İlk olarak Shewhart tarafından geliştirilen kontrol
grafiklerinin temel yapısı normal dağılıma dayanır.
Değişken değerlerinin;
• ±2σ’lık alanda bulunması
olasılığı %95,45
• ±3σ’lık alanda bulunması
olasılığı %99,73’tür.
• Seçilen herhangi bir birimin
±3σ’lık alanın dışında kalması
olasılığı (1-0,9973)=0,0027’dir.
-3σ
-2σ
Ortalama
%95.45
%99.73
+2σ +3σ
Değişkenlik
• Bir prosesten elde edilen ürünler, aynı yöntem
ve makinelerin kullanımına rağmen kalite
özellikleri birbirinin tıpa tıp aynı olmayıp her
zaman birbirinden az da olsa farklılık
gösterebilir.
• Değişkenliğin iki ana nedeni vardır.
1. Genel nedenler
2. Özel nedenler
Kontrol Grafikleri
• Genel nedenlerin etkisiyle ortaya çıkan
değişkenlik kontrol sınırları içinde kalır.
• Özel nedenlerin varlığı prosesin kontrol dışına
çıkması sonucunu yaratır.
Kontrol Grafikleri
• Kontrol sınırları arasında kalan bir nokta sürecin kontrol
altında olduğunu gösterir.
• Herhangi bir şey yapmak gerekmez
• Kontrol sınırları dışında kalan bir nokta sürecin kontrol
altında olmadığını gösterir
• Nedeni bulunabilir sorunların bulunması ve elimine
edilmesi için araştırılma ve düzeltici eylemlerin
yapılmasını gerektirir.
Kontrol Grafikleri
• Shewart tarafından geliştirilmiştir.
• Küçük örneklem hacimlerinde bile anakütle
parametreleri hakkında tutarlı tahminler
vermektedir.
• Her kontrol grafiği tek bir süreci çözümlemek
üzere kullanılır.
• Herhangi bir ürünün kalite özelliklerinin
değerlendirme şekli, hangi tür kontrol
grafiğinin kullanılacağını belirler.
Örnek Büyüklüğü ve Örnekleme Frekansı
Ortalama Koşum Uzunluğu
• Ortalama koşum uzunluğu (run length) (ARL) uygun
örnek büyüklüğünün ve örnekleme frekansının
belirlenmesi açısından çok önemlidir.
• p = süreç kontroldeyken bir noktanın kontrol sınırları
dışına düşme olasılığı olsun.
1
ARL
p
Örnek Büyüklüğü ve Örnekleme Frekansı
Örnek
• Ortalamadan 3 standart sapma uzaklığında
kontrol sınırları olan bir problem
düşünün.Kontrol sınırları dışında kalan
noktaların olasılığı yine 0.0027 (yani, p =
0.0027). Dolayısıyla, ortalama koşum
uzunluğu;
1
ARL
370
0.0027
Örnek Büyüklüğü ve Örnekleme Frekansı
ARL bize ne söylüyor?
• Ortalama koşum uzunluğu bize örnek alma zamanı
uzunluğunu verir, ki kontrol sınırları dışında kalacak
bir noktadan önce örnek alma işlemi yapılabilsin. Bu
değer ne kadar büyükse o kadar iyidir.
• Bizim problemimiz için, süreç kontrol altında olsa
bile ortalama olarak her 370 örnekte bir kontrol dışı
sinyali yaratılacaktır.
Örnek Büyüklüğü ve Örnekleme Frekansı
Ortalama Sinyal Zamanı
• Bazen kontrol şemalarının performansını
ortalama sinyal zamanı (ATS) ile ifade
etmek daha uygun bir yoldur. Yani
örnekler sabit aralıklar ile alınır, h saat
aralığı ile.
ATS ARL(h)
Örnek Büyüklüğü ve Örnekleme Frekansı
•
(hard-bake) sertlik fırınlama sürecini düşünelim. Eğer süreç
ortalaması 1.725 mikron ise, kontrol sınırları arasında kalma
olasılığı yaklaşık olarak 0.50 olur. Dolayısıyla, p 0.50 olur ve
kontrol dışı ortalama koşum uzunluğu (ARL);
l
Eğer h=1 saat ise, ortalama değişim zamanı şöyle
saptanır:
Örnek Büyüklüğü ve Örnekleme Frekansı
•
l
Bunun kabul edilemez olduğunu varsayalım. Bu durumun üstesinden
gelmenin bir yolu daha sık örnek almaktır. Örneğin, eğer biz yarım
saatte bir örnek alırsak, bu durumda ortalama sinyal zamanı
ATS = ARL1 h = 2(1/2) = 1 olur.
İkincisi, olasılık örnek büyüklüğünü arttırmaktır. Örneğin,
n=10 olursa, süreç ortalaması 1.725 mikron olduğunda xbar’ın kontrol sınırları içine düşme olasılığı yaklaşık olarak
0.1 mikron olacaktır, dolayısıyla p = 0.9 olacaktır. Yani ARL1
aşağıdaki gibi olacaktır
Veri Tipleri
• Nicel, Ölçülebilen özellikler (değişken nicelikler):
Sayısal olarak ölçülebilir ve sürekli bir ölçek üzerinde
rakamsal olarak ifade edilebilir özelliklerdir.
Örnek; uzunluk, hacim, ağırlık, sıcaklık vb.
Kalite özelliğini tasvir etmede merkezi eğilim ölçülerinden
aritmetik ortalama, dağılım ölçülerinden standart sapma ve
açıklık kullanılır.
• Nitel, Ölçülemeyen özellikler (vasıflar):
Sayısal olarak ölçülemeyen ancak kusurlu-kusursuz olarak
sınıflandırılabilen özelliklerdir.
Kontrol Grafikleri
•
•
•
•
Kontrol grafikleri ikiye ayrılır.
Nicel Kontrol Grafikleri (Variables)
Nitel Kontrol Grafikleri (Attributes)
Alternatif kontrol grafikleri
• Shewhart kontrol grafikleri süreç kontrolünde
veriler durağan ve ilişkisiz olduğunda en etkili
grafiklerdir.
Nicel Kontrol Grafikleri
1. Ortalama ve Aralık Kontrol Grafiği
2. Ortalama ve Standart Sapma Kontrol Grafiği
3. Bireysel Gözlem (I) ve Hareketli Aralık Kontrol
Grafiği (MR)
Nitel Kontrol Grafiği
1.
2.
3.
4.
Kusurlu oranı (p) kontrol grafiği
Kusurlu sayısı (np) kontrol grafiği
Kusur sayısı (c) kontrol grafiği
Birim başına kusur sayısı (u) kontrol grafiği
Alternatif kontrol grafikleri
1. Kümülatif toplam (CUSUM) kontrol grafiği
2. Hareketli ortalama (MA) kontrol grafiği
3. Üstel ağırlıklı Hareketli ortalama (EWMA)
kontrol grafiği
Değişkenler İçin Kontrol Grafikleri
• X-ortalama grafiği
Süreçte işlem gören ya da çıkan parçaların merkezi
eğilimlerini inceler.
• Açıklık (R) grafiği
Kitlenin dağılışında zaman içinde bir değişiklik olup
olmadığını belirler.
• Standart sapma (S) grafiği
Kitlenin zaman içindeki dağılışını inceleyen bir başka
grafik türüdür.
Uygulamada X-ort. grafiği S veya R grafiği ile birlikte
kullanılır.
Belirtici İstatistikler
n
• Ortalama:
– Veri setinin merkezi eğiliminin bir
ölçüsüdür.
x
• Standart Sapma:
– Dağılımdaki her bir değerin
ortalamaya göre ne uzaklıkta
olduğunu gösteren bir ölçüdür.
• Açıklık:
– Bir başka dağılım ölçüsüdür.
– Veri setindeki en büyük ve en
küçük değer arasındaki farkı ifade
eder.
x
i
i 1
n
x X
n
i 1
2
i
n 1
R= Xmax- Xmin
X-ort. ve R Kontrol Grafikleri
Üretimden alınan örneklerin hacimleri 10’dan küçük
olduğunda (n<10) X-ort. grafiği ile birlikte R grafiğinin
kullanılması tercih edilir.
Üretimin doğru bir görünüşünü elde edebilmek için
genellikle 4 veya 5 birimden oluşan 20-25 alt grup
örneklem olarak seçilir.
X-ort. ve R grafiklerinde kontrol sınırları standartların
belli olması ve olmaması durumlarına göre ayrı ayrı
belirlenir.
X-ort. ve R Kontrol Grafikleri
• Standartların belli olması durumu
Bu durumda anakütle ortalaması µ ve standart
sapması σ bilinmektedir.
X-ort grafiği
ÜKS= µ+Aσ
MÇ= µ
AKS= µ-Aσ
R grafiği
ÜKS= D2σ
MÇ= d2σ
AKS= D1σ
X-ort. ve R Kontrol Grafikleri
• Standartların belli olmaması durumu
n birimlik k tane örnek (alt grup) için;
k
X
X
i 1
i
k
X-ort grafiği
ÜKS X A2 R
MÇ X
AKS X A2 R
R
R
i
k
R grafiği
ÜKS RD4
MÇ R
AKS RD3
X-ort. ve R Kontrol Grafikleri
• Bir üretim prosesinden çeşitli zaman aralıklarında rasgele olarak 5’er
birimlik 20 örnek alınmıştır. (n=5, k=20)
• Anakütle ortalaması ve standart sapması bilinmemektedir (standartlar
belli değil).
• Örneklere ait ortalama ve açıklık değerleri aşağıdaki gibidir.
Örnek no
1
2
3
4
5
6
7
8
9
10
X-Ort
170,6
171,2
172
173,6
173
178,8
177,2
181,6
177,8
178,4
R
23
8
22
12
7
8
16
6
6
12
Örnek no
11
12
13
14
15
16
17
18
19
20
X-Ort
180,8
175,8
179,6
178,6
180,2
179,6
177,8
178,6
181,2
178,2
R
9
8
7
6
5
6
10
9
7
9
X-ort. ve R Kontrol Grafikleri
X = (170,6+171,2+...+178,2)/20
= 177,23
R = (23+8+...+9)/20
= 9,85
Kontrol Sınırları;
X-ort Grafiği
ÜKS = 177,23+(0,58)(9,85)
= 182,91
MÇ = 177,23
AKS = 177,23-(0,58)(9,85)
= 171,55
R Grafiği
ÜKS = (2,12)(9,85)
= 20,83
MÇ = 9,85
AKS = (0)(9,85)
=0
Kontrol Sınırları Çarpanları
Kontrol Sınırları Çarpanları
Ortalama
Standart Sapma
Açıklık
Örneklem genişliği (n)
A
A2
A3
C4
B3
B4
B5
B6
d2
D1
D2
D3
D4
2
2,12
1,88
2,66
0,798
0
3,27
0
2,61
1,13
0
3,69
0
3,27
3
1,73
1,02
1,95
0,886
0
2,57
0
2,28
1,69
0
4,36
0
2,58
4
1,5
0,73
1,63
0,921
0
2,27
0
2,09
2,1
0
4,7
0
2,28
5
1,34
0,58
1,43
0,94
0
2,09
0
1,96
2,33
0
4,92
0
2,12
6
1,23
0,48
1,29
0,952 0,03
1,97
0,03
1,87
2,53
0
5,08
0
2
7
1,13
0,42
1,18
0,959 0,12
1,88
0,11
1,81
2,7
0,21
5,2
0,08
1,93
8
1,06
0,37
1,1
0,965 0,19
1,82
0,18
1,75
2,85
0,31
5,31
0,14
1,86
9
1
0,34
1,03
0,969 0,24
1,76
0,23
1,71
2,97
0,55
5,34
0,18
1,82
10
0,95
0,31
0,98
0,973 0,28
1,72
0,28
1,67
3,08
0,69
5,47
0,22
1,78
11
0,91
0,29
0,93
0,975 0,32
1,68
0,31
1,64
3,17
0,81
5,53
0,26
1,74
12
0,87
0,27
0,89
0,978 0,35
1,65
0,35
1,61
3,26
0,92
5,59
0,28
1,72
13
0,83
0,25
0,85
0,979 0,38
1,62
0,38
1,59
3,34
1,03
5,65
0,31
1,69
14
0,8
0,24
0,82
0,981 0,41
1,59
0,4
1,56
3,41
1,12
5,69
0,33
1,67
15
0,78
0,22
0,79
0,982 0,43
1,57
0,42
1,54
3,47
1,21
5,74
0,35
1,65
X-ort. ve R Kontrol Grafikleri
X Bar-Control Chart
R-Control Chart
184,39
30
25
180,81
20
177,23
15
UKS= 20,83
olcumler
10
Ort = 9,85
UKS = 182,91
173,65
Ort = 177,23
170,07
AKS = 171,55
1
3
2
5
4
Sigma level: 3
7
6
9
8
11
10
13
12
15
14
17
16
AKS = ,00
0
olcumler
1
19
18
5
20
3
2
5
4
Sigma level: 3
7
6
9
8
11
10
13
12
15
14
17
16
19
18
20
XR ÇİZELGESİ ÖRNEK 1/7
TARİH
ÖRNEK DEĞERLERİ
X1
X2
X3
X
X
R
X4
MAYIS 1
2
3
4
5
6
Geri Dön
XR ÇİZELGESİ ÖRNEK 2/7
TARİH
ÖRNEK DEĞERLERİ
X1
X2
X3
X4
MAYIS 1
65
64
67
64
2
63
66
65
63
3
62
67
64
66
4
63
65
67
65
5
58
64
61
59
6
59
60
64
58
XX
R
Geri Dön
XR ÇİZELGESİ ÖRNEK 3/7
TARİH
ÖRNEK DEĞERLERİ
XX
X1
X2
X3
X4
MAYIS 1
65
64
67
64
65
2
63
66
65
63
64
3
62
67
64
66
64
4
63
65
67
65
65
5
57
63
61
59
62
6
59
60
64
58
61
R
Geri Dön
XR ÇİZELGESİ ÖRNEK 4/7
X 63,3
TARİH
R 4,33
ÖRNEK DEĞERLERİ
XX
R
X1
X2
X3
X4
MAYIS 1
65
64
67
64
65
3
2
63
66
65
63
64
3
3
62
67
64
66
64
5
4
63
65
67
65
65
4
5
57
63
61
59
62
6
6
59
60
64
58
61
6
X-ort. ve R Kontrol Grafikleri
• Standartların belli olmaması durumu
n birimlik k tane örnek (alt grup) için;
k
X
X
i 1
i
k
X-ort grafiği
ÜKS X A2 R
MÇ X
AKS X A2 R
=
R
R
i
k
R grafiği
ÜKS RD4
MÇ R
AKS RD3
Kontrol Sınırları Çarpanları
Kontrol Sınırları Çarpanları
Ortalama
Standart Sapma
Açıklık
Örneklem genişliği (n)
A
A2
A3
C4
B3
B4
B5
B6
d2
D1
D2
D3
D4
2
2,12
1,88
2,66
0,798
0
3,27
0
2,61
1,13
0
3,69
0
3,27
3
1,73
1,02
1,95
0,886
0
2,57
0
2,28
1,69
0
4,36
0
2,58
4
1,5
0,73
1,63
0,921
0
2,27
0
2,09
2,1
0
4,7
0
2,28
5
1,34
0,58
1,43
0,94
0
2,09
0
1,96
2,33
0
4,92
0
2,12
6
1,23
0,48
1,29
0,952 0,03
1,97
0,03
1,87
2,53
0
5,08
0
2
7
1,13
0,42
1,18
0,959 0,12
1,88
0,11
1,81
2,7
0,21
5,2
0,08
1,93
8
1,06
0,37
1,1
0,965 0,19
1,82
0,18
1,75
2,85
0,31
5,31
0,14
1,86
9
1
0,34
1,03
0,969 0,24
1,76
0,23
1,71
2,97
0,55
5,34
0,18
1,82
10
0,95
0,31
0,98
0,973 0,28
1,72
0,28
1,67
3,08
0,69
5,47
0,22
1,78
11
0,91
0,29
0,93
0,975 0,32
1,68
0,31
1,64
3,17
0,81
5,53
0,26
1,74
12
0,87
0,27
0,89
0,978 0,35
1,65
0,35
1,61
3,26
0,92
5,59
0,28
1,72
13
0,83
0,25
0,85
0,979 0,38
1,62
0,38
1,59
3,34
1,03
5,65
0,31
1,69
14
0,8
0,24
0,82
0,981 0,41
1,59
0,4
1,56
3,41
1,12
5,69
0,33
1,67
15
0,78
0,22
0,79
0,982 0,43
1,57
0,42
1,54
3,47
1,21
5,74
0,35
1,65
XR ÇİZELGESİ ÖRNEK 5/7
Geri Dön
X-ort. ve S Kontrol Grafikleri
Üretimden alınan örneklerin büyüklükleri 10 dan fazla (n>10)
olduğunda R grafiği yerine S grafiği kullanılır.
n>10 durumunda R’nin etkinliği, dolayısıyla güvenilirliği azaldığından dağılım
ölçüsü olarak standart sapma tercih edilir.
X-ort. ve S grafikleri için de standartların belli olması ve olmaması durumu söz
konusudur.
X-ort. ve S Kontrol Grafikleri
• Standartların belli olması durumu
Anakütle ortalaması µ ve standart sapması σ
olmak üzere;
X-ort grafiği
ÜKS= µ+Aσ
MÇ= µ
AKS= µ-Aσ
S grafiği
ÜKS= B6σ
MÇ= C4σ
AKS= B5σ
X-ort. ve S Kontrol Grafikleri
• Standartların belli olmaması durumu
n birimlik k tane örnek için;
=S
S
i
k
X-ort grafiği
ÜKS= X+A3
MÇ= X
AKS= X -A3
S
n
n 1
S grafiği
ÜKS= B4
MÇ=
AKS= B3
X-ort. ve S Kontrol Grafikleri
•
•
•
Bir üretim prosesinden 10’ar birimlik 15 örnek şansa bağlı olarak alınmıştır. (n=10,
k=15). Bu örneğin gerçekleştirilmesi için n=10 durumunda ortalama ve standart sapma
grafiği çizilmiştir. Normal şartlar altında, n=10 olduğunda ortalama aralık kontrol grafiği
çizilir.
Örneklerin alındığı anakütlenin ortalamasının 54 ve standart sapmasının 2 olduğu
bilinmektedir (standartlar belli: µ=54, σ=2).
Örneklere ait ortalama ve standart sapma değerleri aşağıdaki gibidir.
Örnek no
1
2
3
4
X-Ort
53,9
53,8
53,9
54,3
S
2,47
2,49
3,07
1,34
5
6
7
8
9
10
53,8 53,5 53,7
55,5
54,8
54,1
1,81 1,58 1,16
1,65
1,14
1,45
Örnek no
11
12
13
14
15
X-Ort
55,1
55
54,6
53,5
54
S
1,85
2,31
0,84
1,51
2,16
X-ort. ve S Kontrol Grafikleri
X-ort Grafiği
ÜKS= µ+Aσ = 54+(0,95)2
=55,9
MÇ= µ= 54
AKS= µ-Aσ = 54-(0,95)2
= 52,1
S Grafiği
ÜKS= B6σ =(1,67)2
=3,34
MÇ= C4σ =(0,973)2
=1,95
AKS= B5σ =(0,28)2
= 0,56
Kontrol Sınırları Çarpanları
Kontrol Sınırları Çarpanları
Ortalama
Standart Sapma
Açıklık
Örneklem genişliği (n)
A
A2
A3
C4
B3
B4
B5
B6
d2
D1
D2
D3
D4
2
2,12
1,88
2,66
0,798
0
3,27
0
2,61
1,13
0
3,69
0
3,27
3
1,73
1,02
1,95
0,886
0
2,57
0
2,28
1,69
0
4,36
0
2,58
4
1,5
0,73
1,63
0,921
0
2,27
0
2,09
2,1
0
4,7
0
2,28
5
1,34
0,58
1,43
0,94
0
2,09
0
1,96
2,33
0
4,92
0
2,12
6
1,23
0,48
1,29
0,952
0,03
1,97
0,03
1,87
2,53
0
5,08
0
2
7
1,13
0,42
1,18
0,959
0,12
1,88
0,11
1,81
2,7
0,21
5,2
0,08
1,93
8
1,06
0,37
1,1
0,965
0,19
1,82
0,18
1,75
2,85
0,31
5,31
0,14
1,86
9
1
0,34
1,03
0,969
0,24
1,76
0,23
1,71
2,97
0,55
5,34
0,18
1,82
10
0,95
0,31
0,98
0,973
0,28
1,72
0,28
1,67
3,08
0,69
5,47
0,22
1,78
11
0,91
0,29
0,93
0,975
0,32
1,68
0,31
1,64
3,17
0,81
5,53
0,26
1,74
12
0,87
0,27
0,89
0,978
0,35
1,65
0,35
1,61
3,26
0,92
5,59
0,28
1,72
13
0,83
0,25
0,85
0,979
0,38
1,62
0,38
1,59
3,34
1,03
5,65
0,31
1,69
14
0,8
0,24
0,82
0,981
0,41
1,59
0,4
1,56
3,41
1,12
5,69
0,33
1,67
15
0,78
0,22
0,79
0,982
0,43
1,57
0,42
1,54
3,47
1,21
5,74
0,35
1,65
X-ort. ve S Kontrol Grafikleri
X Ortalama Grafiği
57
56
55
54
53
52
51
S Grafiği
Ortalama
ÜKS
MÇ
AKS
0
2
4
6
8 10 12 14 16
Örnek No
3,5
3
2,5
2
1,5
1
0,5
0
S.sapma
ÜKS
MÇ
AKS
0 2 4 6 8 10 12 14 16
Örnek No
Özellikler (Nitel) İçin Kontrol Grafikleri
• p (kusurlu oranı) grafiği
Prosesten alınan örneklerin kusurlu oranlarını inceleyen grafik
türüdür.
• Stabilize p grafiği
Örnek ölçümlerinin eşit olmaması durumunda kullanılan grafiktir.
• np (kusurlu sayısı) grafiği
Kusurlu sayılarıyla oluşturulan grafiklerdir.
• c (örnek başına kusur sayısı) grafiği
Her bir örnek için toplam kusur sayıları dikkate alınarak
hazırlanan kontrol grafiğidir.
• u (birim başına kusur sayısı) grafiği
Tek bir birimdeki hataları incelemek için kurulan kontrol
grafiğidir.
p (kusurlu oranı) Grafiği
p grafiklerinde, oran söz konusu olduğu için, üretim
sürecinden daha büyük hacimli örnekler alınmalıdır.
Kriter olarak; np>1 olacak şekilde n’in tespit
edilmesi tavsiye edilir. Örneğin, kusurlu oranı p=0.05
ise np>1 durumunun sağlanması için n>20 olmasına
dikkat edilmelidir.
Anakütle kusurlu oranı belli değilse şansa bağlı
olarak alınacak yeterince büyük bir örnekteki kusurlu
oranı esas alınarak örnek büyüklükleri ayarlanır.
p (kusurlu oranı) Grafiği
Birinci örnekteki kusurlu sayısı x1, ikinci örnekteki x2,..,
k’inci örnekteki kusurlu sayısı xk olmak üzere bu
örneklerdeki kusurlu oranları;
p1=x1/n, p2=x2/n, ......, pk=xk/n şeklindedir.
Ortalama kusurlu oranı; p = (p1+p2+...+pk)/ k
Kontrol sınırları;
ÜKS p 3 p(1 p) n
MÇ =
p
AKS p 3 p(1 p) n
p (kusurlu oranı) Grafiği
• Bir üretimden 50’şer birimlik 20 örnek alınmıştır. (n=50, k=20)
• Anakütlenin kusurlu oranı bilinmemektedir (standart belli değil).
• Her bir örnekteki kusurlu sayıları ve kusurlu oranları aşağıdaki şekilde
tespit edilmiştir.
Örnek no
1
2
3
4
5
6
7
8
9
10
K. sayısı
9
4
5
16
10
15
7
9
5
12
K. oranı
0.18
0.08
0.1
0.32
0.2
0.3
0.14
0.18
0.1
0.24
Örnek no
11
12
13
14
15
16
17
18
19
20
Toplam
K. sayısı
10
17
14
19
12
8
10
6
12
8
208
K. oranı
0.2 0.34 0.28 0.38 0.24 0.16
0.2
0.12 0.24 0.16
4.16
p (kusurlu oranı) Grafiği
Birinci örnekteki kusurlu oranı; p1=9/50=0.18
İkinci örnekteki kusurlu oranı; p2=4/50=0.08
.
.
Ortalama kusurlu oranı; p = (0.18+0.08+...+0.16)/20
= 4.16/20= 0.21
Kontrol sınırları;
ÜKS = 0.21+3
MÇ = 0.21
= 0.38
(0.21)(0.79) / 50
AKS = 0.21-3
= 0.04
(0.21)(0.79) / 50
p (kusurlu oranı) Grafiği
p-Control Chart
,4
,3
,2
KUSURLU
UKS = ,38
,1
M C = ,21
0,0
AKS = ,04
1
3
2
5
4
Sigma level: 3
7
6
9
8
11
10
13
12
15
14
17
16
19
18
20
np (kusurlu sayısı) Grafiği
np grafiklerinde kusurlu oranları yerine kusurlu
sayıları kullanılır. Örnek oranlarının hesaplanmasına
gerek duyulmadığı için p grafiğine göre daha kolay
gelebilmektedir. Şekil olarak p grafiğinin aynısıdır.
Sadece dik eksen kusurlu oranı yerine kusurlu sayısını
temsil eder.
x
p=
Ortalama kusurlu oranı;
nk
Kontrol sınırları; ÜKS = np +3 n p(1 p)
MÇ = n p
AKS = n p -3 n p(1 p)
np (kusurlu sayısı) Grafiği
• Bir piston imalathanesinin üretiminden 100’er birimlik 15 örnek alınmıştır.
(n=100, k=15)
• Anakütlenin kusurlu oranı bilinmemektedir (standart belli değil).
• Her bir örnekteki kusurlu sayıları aşağıdaki gibidir.
Örnek no
1
2
3
4
5
6
7
8
9
10
Kusurlu
sayısı
8
16
4
0
6
2
8
6
4
5
Örnek no
11
12
13
14
15
Toplam
Kusurlu
sayısı
5
0
7
8
14
93
np (kusurlu sayısı) Grafiği
Ortalama kusurlu oranı;
p
=
93 =0.062
100 x15
Kontrol sınırları;
ÜKS = 100(0.062)+3 100(0.062)(0.938)
= 13.43
MÇ = 100(0.062) = 6.20
AKS = 100(0.062)-3 100(0.062)(0.938)
= -1.03= 0
np (kusurlu sayısı) Grafiği
np-Control Chart
20
15
10
kusur
UKS = 13,43
5
M C = 6,20
0
AKS = ,00
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
orne k no
Sigma level: 3
c Kontrol Grafiği
(Örnek başına kusur sayısı)
c grafiklerinde üretilen birimlerin kalite kontrolünde, her
bir örnekte rastlanan toplam kusur sayıları esas alınır.
Örnek, tek bir parça ürün ya da parçanın bir kısmı olabilir.
k; alt grup sayısı olmak üzere her bir alt grupta n=1
olma durumu söz konusudur.
k
Ortalama kusur sayısı;
Kontrol sınırları;
c
c
i 1
k
ÜKS c 3 c
MÇ = c
AKS c 3 c
i
c Kontrol Grafiği
(Örnek başına kusur sayısı)
• Bir firmanın ürettiği buzdolaplarından 20 tanesi alınmıştır. (k=20)
• Geçmiş verilere dayanılarak hesaplanmış bir c değeri yoktur (standart
belli değil).
• Her bir buzdolabındaki toplam kusur sayısı tespit edilerek aşağıdaki
tablo düzenlenmiştir.
Örnek no
1
2
3
4
5
6
7
8
9
10
Kusur
sayısı
4
3
5
7
2
8
1
4
3
5
Örnek no
11
12
13
14
15
16
17
18
19
20
Kusur
sayısı
6
6
3
1
2
2
5
4
0
3
c Kontrol Grafiği
(Örnek başına kusur sayısı)
Ortalama kusur sayısı;
c = ∑ci / k =(4+3+5+...+3)/20
= 3,7
Kontrol sınırları;
ÜKS = 3,7+3 3,7
= 9,47
MÇ =3,7
AKS = 3,7-3 3,7
= -2,07 =0
c kontrol Grafiği
(Örnek başına kusur sayısı)
c-Control Chart
10
8
6
4
kusur
UKS = 9,47
2
M C = 3,70
0
AKS = ,00
1
3
2
5
4
Sigma level: 3
7
6
9
8
11
10
13
12
15
14
17
16
19
18
20
u-Kontrol Grafiği
(Birim başına kusur sayısı)
u grafiklerinde her bir birimde rastlanan ortalama kusur
sayıları işlenir. Buna ek olarak bazı durumlarda alt gruplar
farklı sayılarda birimlerden oluşabilirler.
Alt grupları oluşturan birim sayıları farklılık gösterdiğinde
izlenebilecek iki yol vardır:
– Ortalama bir n değeri hesaplamak,
– Değişen n değerlerine göre ayrı ayrı kontrol sınırları
belirlemek.
u-Kontrol Grafiği
(Birim başına kusur sayısı)
Uygulamalar için birim başına gerçek hata sayısı u
bilindiğinde (standart belli iken), bu değer kontrol
sınırlarını hesaplamada kullanılır. Bilinmediğinde ise
birim başına ortalama hata sayısı (ū) hesaplanır.
U
=
Kontrol sınırları;
c
n
ÜKS u 3 u n
MÇ u
AKS u 3 u n
u-Kontrol Grafiği
(Birim başına kusur sayısı)
• Bir dokuma fabrikasında günlük üretilen top kumaşlardaki kusurları
belirlemek amacıyla %100 muayene yapılmıştır.
• 10 günlük süreçte tespit edilen kusurlu kumaş topu sayıları ve bunlardaki
kusur sayıları aşağıdaki gibidir.
• Gerçek kusur sayısı olan u değeri bilinmemektedir (standart belli değil).
Gün
1
2
3
4
5
6
7
8
9
10
Kumaş
topu s.(n)
20
20
20
21
22
22
23
33
23
21
Kusur
sayısı (c)
27
23
30
28
29
31
37
29
36
27
u-Kontrol Grafiği
(Birim başına kusur sayısı)
Birim başına ortalama kusur sayısı; ū= ∑c / ∑n
= 297/225= 1,32
Gün
Kumaş topu
Sayısı (n)
Kusur
Sayısı (c)
1
2
3
4
5
6
7
8
9
10
Toplam
20
20
20
21
22
22
23
33
23
21
225
27
23
30
28
29
31
37
29
36
27
297
ui=ci/ni
3 ū/ni
ÜKS
AKS
1,35
1,15
1,50
1,33
1,32
1,41
1,61
0,88
1,57
1,29
0,77
0,77
0,77
0,75
0,73
0,73
0,72
0,60
0,72
0,75
2,09
2,09
2,09
2,07
2,05
2,05
2,04
1,92
2,04
2,07
0,55
0,55
0,55
0,57
0,59
0,59
0,60
0,72
0,60
0,59
u-kontrol grafiği
(Birim başına kusur sayısı)
u-Control Chart
2,5
2,0
1,5
1,0
kusur
UKS
,5
M C = 1,32
0,0
AKS
1
2
Sigma level: 3
3
4
5
6
7
8
9
10
Kontrol Şemalarının Yorumlanması
•
Kontrol şeması üzerinde sürece ait bir kalite karakteristiğinin zaman içerisindeki
davranışı (değişimi) görsel olarak izlenebilir.
•
Kontrol şeması yardımıyla süreci etkileyen doğal sebeplerin meydana getirdiği
(önlenemeyen) değişkenliğin varlığı ve sınırları belirlenir. Üründe gözlenen
değişkenliğin bu sınırlar arasında olup olmadığı gözlenir. Gözlemler bu sınırlar
dışına çıkıyorsa özel (önlenebilir) bir sebebin süreci etkilediği anlaşılır. Böylece bu
özel sebeplerin bulunup süreci etkilemesi engellenebilir.
•
Bir grup ortalamasının sınırlar dışına düşmesi sürecin kontrol dışına çıktığını
gösteren tek işaret değildir. Bazı durumlar da tüm ortalamalar kontrol sınırları
arasına düşmesine rağmen sürecin istatistiki olarak kontrolden çıktığına karar
verilebilir.
Kontrol Şemalarının Yorumlanması
Herhangi bir gözlem ÜKS’ın üstünde veya
AKS’ının altında kalırsa (9a),
Art arda 8 gözlem MÇ’inin altında veya üstünde
ise (9b),
Art arda 6 gözlemin artması veya azalması (9c),
Art arda alınan 3 gözlemden 2 tanesinin
MÇ’inin altında veya üstündeki bölgenin dış
üçte birlik alanına girmesi (A bölgesi) (9d),
Art arda alınan 5 gözlemden 4 tanesinin
MÇ’inin altında veya üstündeki bölgenin dış
üçte ikilik alanına girmesi (A veya B bölgesi)
(9e),
Bu beş durumdan biri gerçekleşirse süreç kontrol altında değildir
Örnekler
• Kontrol dışı
C: 55-72
B: 72-89
A: 89-105
C: 55-38
B: 38-21
A: 21-5
Süreç Yeterlilik Analizi
• Süreç yeterliliği istatistiksel bir ölçüt olup
müşteri beklentilerine (spesifikasyonlarına)
göre bir sürecin ne kadar değişkenlik
gösterdiğini özetler.
Süreç Yeterlilik İndeksleri
• Cp: Şartname limitleri ile proses kontrol
limitleri arasındaki ilişkiyi gösterir.
• Tasarım tolerans aralığının, sürece
uygunluğunu ölçmek için kullanılır.
Maksimum izin verilen tasarım aralığı
Cp=
Sürecin normal dağılımı
(USL ASL)
=
6
Süreç Yeterlilik İndeksleri
• Cpk: Proses ortalamasının (X), hedef değere
göre konumunu belirler. Proses ortalamasının
hedef değerden ne kadar uzakta olduğunu
gösterir.
C pk min ((USL ) / 3 ), ( ALS ) / 3 )
Cp>1,33
1<Cp<1,33
Cp<1
Cpk>1,33
1<Cpk<1,33
Cpk<1
Proses yeterli
Proses marjinal olarak yeterli,
daha yakından izlenmeli
Proses yetersiz
(proses değişkenliğinin
azalması gerekli)
Proses şartname limitlerini
karşılıyor.
Proses marjinal olarak
şartname limitlerini karşılıyor.
Proses ortalaması hedeften
uzaklaştıkça prosesin hata
yüzdesi artabilir.
Proses şartname limitlerini
karşılamıyor. Proses ortalaması
hedef değerden uzakta.
KABUL-ÖRNEKLEME PROBLEMİ
Kabul örneklemesi için tipik uygulama; parti düzenlenmesi bazı durumlarda ise parti
tanımlanmasıdır,
inceleme faaliyetlerinin alınması için,
* Kabul edilmiş partiler, üretime konulur.
* Reddedilmiş partiler, tedarikçiye iade edilir ya da diğer parti düzenlemeleri için kullanılır.
Örnekleme metodları, üretimin çeşitli aşamalarında kullanılabilir.
Örneklemenin en önemli 3 amacı :
1. Kabul örneklemesinin amacı, parti kalitesinin tahmini değil parti tanımlanmasıdır. Kabul
örnekleme planlarının çoğu tahmin amaçlı tasarlanmamıştır.
2. Kabul-örnekleme planları, kalite kontrolün herhangi direkt şeklini vermez. Kabul
örneklemesi basitçe partileri kabul eder veya reddeder. Bütün partiler eşit kalitede olsalar
bile; örnekleme, bazı partileri kabul eder, bazılarını reddeder. Kabul edilen partiler,
diğerlerinden daha iyi değildir. Proses kontrolleri, kalitenin kontrolünü ve sistematik olarak
iyileştirilmesini sağlar, fakat kabul örneklemesi sağlamaz.
3. Kabul örneklemesinin en etkili kullanımı, ürünün kalitesinin denetlenmesi değil, bir
denetleme aracı olarak prosesin çıktılarının, ihtiyaçları karşılamasını sağlamaktır.
KABUL-ÖRNEKLEME PROBLEMİ
Kabul örneklemesi aşağıdaki durumlarda daha çok fayda sağlar.
1.
Test etmenin tahrip edici olması,
2.
%100 kontrolün maliyetinin son derece yüksek olması,
3.
%100 kontrolün teknolojik olarak uygun olmaması ya da üretim programının aksamasına
neden olabilecek çok fazla zamana ihtiyaç duyulması,
4.
Kontrol edilecek çok fazla birimin bulunması ve kontrol hata oranının yeterli düzeyde yüksek
olması, %100 kontrolle yüksek yüzdede hatalı birimin geçmesine neden olabilir, bu örnekleme
planı ile de çıkarılabilir.
5.
Tedarikçinin mükemmel bir kalite geçmişi varsa ve kontrolde %100’den bir miktar azalmaya
eğilim varsa fakat tedarikçinin proses yeteneği oldukça düşükse, kontrol yapmama memnun
etmeyici bir alternatiftir.
6.
Potansiyel ciddi üretim risk eğilimleri varsa, buna rağmen tedarikçinin prosesi memnun edici
ise sürekli ürünü gözlemleyen bir program ihtiyacı doğar.
Örneklemenin Avantaj ve Dezavantajları
Kabul örneklemesi, %100 kontrol ile karşılaştırıldığı zaman aşağıdaki avantajlara sahip olduğu
görülür.
1.
Genellikle daha az pahalıdır, çünkü daha az kontrol vardır.
2.
Daha az müdahale vardır, tahribatı azaltır.
3.
Tahrip edici testlerde uygundur.
4.
Kontrol faaliyetlerinde, daha az personel yer alır.
5.
Kontrol hata miktarını önemli düzeyde azaltır.
6.
Basit hatalara rağmen, partinin tümünün reddedilmesi, tedarikçinin kalite iyileştirmeleri
yapmasında etkili motivasyon sağlar.
Kabul örneklemesi bazı dezavantajlara sahiptir. Bunlar aşağıdaki gibidir.
1.
“Kötü” partileri kabul etme, “İyi” partileri reddetme riskini taşır.
2.
Ürün veya ürünü üreten proses hakkında, daha az bilgi oluşur.
3.
Kabul örneklemesi, %100 kontrolde gerekmediği kadar planlama ve kabul-örnekleme prosedürü
dokümantasyonu gerektirir.
Örneklemenin Avantaj ve Dezavantajları
Kabul örneklemesinin; iki uç olan %100 kontrol ve kontrol yapılmaması arasında orta bir
seviye dir. Bu, ürünü üreten, imalat prosesinde iki uç noktayı ayıran, yeterli bilgiyi içeren bir
metodolojidir.
Kabul örnekleme planı ile izole edilmiş bir partide, uygulamada kalitenin direkt kontrol
edilmemesine rağmen, bu plan, tedarikçiden gelen parti gruplarına uygulandığı zaman, hem
partilerin üreticisi için hem de tüketici için korumayı sağlayan anlam taşır. Aynı zamanda
partileri üreten prosesi içeren, birikimli kalite geçmişini verir ve proses kontrolünde faydalı
olan, tedarikçinin tesisinin yeterli olup olmadığı gibi geri bildirimler verir. Sonuç olarak,
tedarikçi için üretim prosesinin iyileştirilmesi, ekonomik veya psikolojik baskı oluşturur.
Örnekleme Planlarının Çeşitleri
•
Temel bir sınıflandırma, veri çeşidine göredir. Değişkenler ve nitelikler.
•
Diğeri ise karar için ihtiyaç duyulan örnek sayılarına dayanır.
* Tek-örnekleme planları
* Çift-örnekleme planları
* Çoklu-örnekleme planları
* Sıralı-örnekleme planları
•
Tek-, çift-, çoklu- ve sıralı-örnekleme planları eşdeğer sonuçlar üretmek için tasarlanır. İçerikte göz
önünde bulundurulan faktörler :
* İdari yeterlilik
* Plan tarafından üretilen bilginin çeşitleri
* Plan tarafından ihtiyaç duyulan ortalama kontrol miktarı
* Üretim akışında prosedür etkisi
Parti Oluşturulması
Kontrol için partilerin oluşturulması, önemli koşulları içerir;
1. Partiler, homojen olmalı (Partideki üniteler, aynı makine , aynı operatörler ve ortak
hammaddeden üretilmeli)
2. Büyük partiler, küçük partilere tercih edilir. (Ekonomik etkinlik)
3. Partiler, hem üretici, hem de tüketicisi tarafından kullanılan malzeme taşıma sistemleriyle
uyumlu olmalı
Rasgele Örnekleme
Kontrol için seçilen birimler, rasgele seçilmeli ve partideki bütün birimleri temsil etmelidir
Birimler, her kübün içerisinden seçilmelidir.
Şekil 1. Partinin katmanlaştırılması
Kabul Örneklemesi Kullanımının Kuralları
•
Kabul-örneklemesi planı, örnek büyüklüğü ve parti tanımlanması için kabul/red kriterini içerir.
•
Kabul-örneklemesi şeması, %100 kontrol ve kabul örnekleme miktarı ile ilgili; parti büyüklüğünü,
örnek büyüklüğünü ve kabul/red kriterlerini içeren kabul-örneklemesi planı, bir prosedürler
kümesidir.
•
Bir örnekleme sistemi, bir veya birden fazla şemanın birleşimidir.
Nitelikler için Tek-Örnekleme Planları Tek-Örnekleme Planı Tanımı
N büyüklüğündeki bir partinin kontrol için alındığını farzedin. n örnek büyüklüğündeki ve c kabul
numaralı tek-örnekleme planı tanımlanır. Bu yolla, eğer parti büyüklüğü N=10.000 ise örnekleme
planı,
n=89
c=2
10.000 büyüklüğüne sahip bir partiden, n=89 birimin kontrol edildiği, d kadar uymayan veya kusurlu
ürün tespit edildiği anlamına gelir. Eğer tespit edilen kusurlu sayısı d, c=2’ye küçük eşitse, parti
reddedilecektir.
Kontrol edilen kalite karakteristiği bir nitelik olduğu sürece, örneklemedeki her birim uymayı ve
uymamayı simgeler. Aynı örnekte bir veya birden fazla nitelik kontrol edilebilir, genellikle, bir veya
birden fazla niteliğe uymayan birim, kusurlu birim olarak söylenebilir. Bu prosedür tek-örnekleme
planı olarak adlandırılır, çünkü parti, n büyüklüğünde bir örneklemedeki sınırlandırılmış bilgide,
tanımlama temellidir.
Operasyon Özellikleri (OC) Eğrisi
Kabul-örnekleme planının önemli bir performans ölçümü operasyon özellikleri eğrisidir.
Bu eğri, partinin kabul edilme olasılığına karşın kusurlu kısmın grafiğini çizer.
Dolayısıyla, OC eğrisi, örnekleme planının ayırt etme kuvvetini gösterir. Belirli bir
kısmı kusurlu olan onaylanmış partilerin kabul edilip,edilmeme olasılığını gösterir.
Kabul edilme olasılığı, Pa
Operasyon Özellikleri (OC) Eğrisi
Kusurlu kısım partisi, p
Şekil 2 Tek-örnekleme planının n=89, c=2, OC Eğrisi
OC eğrisi, örnekleme planının ayırt etme
kuvvetini gösterir. Örneğin, örnekleme
planında n=98, c=2, eğer partiler %2
kusurlu ise kabul edilme olasılığı yaklaşık
olarak 0,74’tür. (Tablo 14.2)
Kusurlu kısım partisi, p
Kabul edilme olasılığı, Pa
Tablo 2 Tek-örnekleme planı için kabul edilme olasılıkları n=89, c=2
Operasyon Özellikleri (OC) Eğrisi
Kabul edilme olasılığı, Pa
Kabul edilme olasılığı, Pa
Kabul edilme olasılığı, Pa
OC eğrilerinde c ve n’nin etkisi
Kusurlu kısım partisi, p
Şekil 3 İdeal OC eğrisi
Kusurlu kısım partisi, p
Kusurlu kısım partisi, p
Şekil 4 Farklı örnekleme büyüklükleri için Şekil 5 OC eğrisinde, kabul edilme sayısında
OC eğrileri
değişkenliğin etkisi
Örnek büyüklüğü ile birlikte OC
eğrisi, ideal OC eğrisine daha çok
benziyor.
Kabul edilme sayısı azaldıkça, OC
eğrisi sola kayıyor. Küçük
değerler kullanan c ile yapılmış
planlar parti kusurlu oranının daha
düşük seviyelerde ayırt edilmesini
sağlar.
Operasyon Özellikleri (OC) Eğrisi
OC Eğrisinde Spesifik Noktalar
•
Tedarikçinin en kötü kalite seviyesine sahip prosesi, tüketici kabul edebileceği ortalama
prosese Kabul Edilebilir Kalite Seviyesi diye adlandırılır (AQL).
* AQL, tedarikçinin üretim prosesinin özelliğidir, örnekleme planının özelliği değildir.
* Tüketici, her zaman örnekleme planını tasarlayacak, böylece OC eğrisi AQL’de kabul
edilebilir yüksek olasılık verir.
•
Düşük kaliteli bireysel partiler için sağlanan koruma (LTPD) parti toleransındaki yüzde kusur
tarafından oluşturulur.
* Aynı zamanda reddedilebilir kalite seviyesi (RQL) ve sınırlı kalite seviyesi diye adlandırılır.
* LTPD, tüketici tarafından belirlenmiş parti seviyesi kalitesidir, örnekleme planının
karakteristiği değildir.
•
Örnekleme planları, AQL ve LTPD noktalarında tanımlanmış performans vermek için
tasarlanmıştır.
Operasyon Özellikleri (OC) Eğrisi
A Tipi ve B Tipi OC Eğrileri
Önceki örneklerde çizilen OC eğrileri, B tipi OC eğrileri olarak adlandırılır. OC eğrilerinin
çiziminde, örneklemelerin büyük bir partiden geldiği veya bir prosesten rasgele seçilmiş partiler dizisinden
geldiği farz edilir. Bu durumda, partinin kabul edilebilirlik olasılığının hesaplanması için binom dağılımı,
tam olarak kullanılabilir bir olasılık dağılımıdır. Böyle bir OC eğrisi, B tipi OC eğrisine dayanır.
A tipi OC eğrileri, sınırlı büyüklükteki parti büyüklüklerinin kabul edilme olasılıklarının
hesaplanması için kullanılır. Parti büyüklüğünün N, örnekleme büyüklüğünün n, kabul edilme sayısının c
dağılımdır.
Kabul edilme olasılığı, Pa
olduğunu varsayalım. Örneklemedeki kusurlu birim sayısının örnekleme dağılımı hipergeometrik
Kusurlu kısım partisi, p
Şekil 6 A tipi ve B tipi OC eğrileri
Operasyon Özellikleri (OC) Eğrisi
OC eğrisi amaçlarının diğer davranışları
Örnekte iki yaklaşımla karşılaştırılan örnekleme planı tasarımlarının, OC eğrisi için mutlak
ayrımlara sahiptir. İki yaklaşım; örnekleme planlarının “0” kabul sayısı ile kullanımı (z=0), parti
Kabul edilme olasılığı, Pa
Kabul edilme olasılığı, Pa
büyüklüğünün sabitlenmiş yüzdesi ile örnekleme büyüklüğünün kullanımı.
Kusurlu kısım partisi, p
Şekil 7 c=0 ile tek-örnekleme planı için OC eğrileri
Kusurlu kısım partisi, p
Şekil 8 Örnekleme büyüklüğü n’in, parti büyüklüğünün
%10’u olan örnekleme planları için OC eğrileri
Belirlenmiş OC Eğrisi ile Tek-Örnekleme Planı Tasarımı
•
Tasarlanacak bir kabul-örnekleme planında temel yaklaşım, OC eğrisinin belirlenmiş iki noktadan
geçmesini içermelidir.
•
Örnekleme planını şu şekilde oluşturmak istediğimizi varsayalım,
Kusurlu kısmı P1 olan parti için 1- α kabul edilme olasılığı,
Kusurlu kısmı P2 olan parti için β kabul edilme olasılığı.
•
Denklem 14-3’ün çözümü, örnekleme büyüklüğü n ve kabul edilme sayısı c’dir.
Denklemlerin çözümü için Şekil 14-9’daki nomograf kullanılabilir.
c’nin olasılığı veya n denemelerindeki az tekrarlananlar
Tek denemede tekrar olasılığı (p)
Belirlenmiş OC Eğrisi ile Tek-Örnekleme Planı Tasarımı
Şekil 9 Binom nomografı
Düzeltici Kontrol
Red
parti
Gelen parti
Kusurlu kısım
0
Çıkan parti
Kontrol
Faaliyeti
Kusurlu kısım P0
Kusurlu kısım p1<p0
Kabul
parti
Kusurlu kısım
P0
Şekil 10 Düzeltici kontrol
Ortalama çıktı kalitesi, örnekleme planının düzeltilmesinde hesaplanır. Ortalama çıktı kalitesi, düzeltici kontrol
uygulanmasıyla sonuçlanan partinin kalitesidir. Kusurlu kısmı p olan prosesten elde edilen uzun sıralı partilerin
kalitesinin ortalama değeridir. Ortalama çıktık kalitesi için bir formül elde etmek basittir (AOQ). Parti
büyüklüğünün N olduğunu ve bütün tespit edilen kusurlu birimlerin yeni birimlerle değiştirildiğini varsayalım.
Böylece N büyüklüğündeki partide,
1. Örneklemedeki n birimleri, kontrolden sonra, kusur içermez, çünkü bütün kusurlular değiştirilmiştir.
2. N – n birimleri, parti reddedildiyse, kusur içermez
3. N – n birimleri, parti kabul edildiyse, p(N-n) kusur içerir.
Düzeltici Kontrol
Böylece, kontrolün çıktı aşamasındaki partiler, ortalama kusurlu kısım diye belirtilebilecek,
Pap(N-n)’a eşit olan kusurlu birimlerin beklenen sayısı, ortalama çıktı kalitesi olarak
adlandırılır.
14-4’deki denklemi açıklamak için, N=10.000, n=89 ve c=2 ve gelen parti kalitesi p=0,01 olduğunu
varsayalım. p=0,01’de, Pa=0,9397 ve AOQ,
Ortalama çıktı kalitesi %0,93 kusurludur. Parti büyüklüğü N, n örnek büyüklüğüne bağlı olarak daha
büyüyecektir. 14-4 denklemini şu şekilde yazabiliriz.
Düzeltici Kontrol
Çıktı partilerinin ortalama kusurlu kısmı
AOQL, eğrideki
maksimum noktadır
Girdi partisi kalitesi (kusurlu kısım), p
Şekil 11 n=89, c=2 için ortalama çıktı kalitesi
Düzeltici Kontrol
Eğer parti kalitesi 0<p<1 ise, parti başına ortalama kontrol miktarı, örnekleme büyüklüğü n ve parti büyüklüğü N arasında
değişecektir. Eğer parti p kalitesine sahipse ve partinin kabul edilme olasılığı Pa ise parti başına ortalama toplama kontrol;
14-6’daki denklemin kullanımını anlamak için, bir önceki örneği hatırlayalım, N=10.000, n=89, c=2 ve p=0,01.
Böylece Pa=0,9397 bulunmasıyla;
Bunun, kusurlu kısmı p=0,01 olan çoğu parti içinden kontrol edilen ortalama birim sayısı
olduğunu unutmayalım.
Ortalama toplam kontrol (ATI)
Düzeltici Kontrol
Kusurlu kısım partisi, p
Şekil 12 n=89, c=2 örnekleme planı için,
(parti büyüklükleri 1.000,5.000 ve 10.000 için)
ortalama toplam kontrol eğrisi
Düzeltici Kontrol
Düzeltici kontrol planının AOQL’si çok önemli bir özelliktir. Tanımlanmış
değerlere sahip AOQL için düzenlenmiş kontrol programlarının tasarımı
mümkündür. Fakat AOQL’nin spesifikasyonu için tek bir örnekleme planı
belirlemek yeterli değildir. Dolayısıyla belirli bir AOQL için yapılan örnekleme
planı seçimi pratikte oldukça yaygındır, buna ek olarak parti kalitesinin belirli bir
seviyesinde minimum ATI’yi sağlar. Parti kalitesi seviyesi çoğunlukla gelen parti
kalitesi seviyesine çok benzer seçilir ve genellikle süreç ortalaması olarak
adlandırılır. Bu planların oluşturulmasındaki prosedür oldukça kolay anlaşılırdır ve
Duncan tarafından örneklendiği gibidir. Genellikle bu prosedürü izlemek
gereksizdir, çünkü AOQL için verilen minimum ATI’yi veren ve süreç ortalaması p
olarak belirlenen örnekleme planı tabloları Dodge ve Roming tarafından
geliştirilmiştir. Bu tabloların kullanımını Bölüm 14-5’de tanımlayacağız.
LTPD noktasında istenilen seviyede koruma sağlayan düzeltici bir denetleme
programı tasarlanması da mümkündür. Bu sayede belirlenmiş süreç ortalaması p
için ortalama toplam denetim minimize edilir. Dodge-Roming örnekleme kontrol
tabloları genellikle LTPD planlarını sağlar. Bölüm 14-5’de belirli
LTPD
korumalarını öneren planların bulunduğu Dodge-Roming tablolarının kullanımı
tartışılacaktır.
İkili, Çoklu ve Sıralı Örnekleme
İkili Örnekleme Planları
•
Bir ikili örnek planı parti hakkında karar vermeden önce belirli koşullar altında ikinci bir
örnek gerektiren bir prosedürdür. Bir ikili örnekleme planı 4 parametre ile tanımlanır:
– n1=ilk örnekteki örnek büyüklüğü
– c1=ilk örnekten kabul edilen sayısı
– n2=ikinci örnekteki örnek büyüklüğü
– c2=her iki örnekten de kabul edilen sayısı
İkili Örnekleme Planları
Örneğin, n1=50, c1=1, n2=100 ve c2=3 olsun. Bu takdirde, ilk rassal
n1=50parçalık partiden örnek seçilir ve örnekteki kusurlu sayısı, d1,
gözlemlenir. Eğer d1≤c1=1 ise, ilk örnek üzerinden parti kabul edilir. Eğer
d1>c2=3 ise, parti ilk örnek üzerinden reddedilir. Eğer c1<d1≤c2 ise, n2=100
örnek büyüklüğüne sahip 2. rassal partiden seçim yapılır, ve ikinci
örnekteki kusurlu sayısı , d2, gözlemlenir. Şimdi hem ilk hem de ikinci
partilerden gözlemlenen kusurlu sayılarından, d1+d2, yola çıkarak parti için
karar verilmelidir. Eğer d1+d2≤c2=3, ise parti kabul edilir. Eğer d1+d2>c2=3,
ise parti reddedilir. Bu ikili örnekleme planı operasyonları Şekil 14-13’de
grafik ile gösterilmiştir.
•
İkili örnekleme planının tekli örnekleme planına göre avantajı kontrol için gerekli toplam
miktarı azaltmasıdır.
•Farz edelim ki; ikili örneklemede ilk örnek tekli örneklemedekinden daha az olsun;
• Eğer parti ilk örnekte kabul veya reddedilir ise; kontrolün maliyeti azalır.
• Ayrıca ikinci örneklemeyi yapmadan reddetmek de olasıdır.
Şimdi, n1=50, c1=1, n2=100 ve c2=3 planı için, OC eğrisi hesaplamalarını örnekleyelim. Eğer
Pa birleşik örnekler üzerinden kabulün olasılığını ve PaI ve PaII de sırasıyla ilk ve ikinci
örneklemelerin kabulünün olasılığını gösteriyor ise;
PaI n1=50 için d1< c1=1 kusurlu gözlemlerinin olasılığıdır.
Eğer p=0.05 gelen partideki kusurlu oranı ise;
İkinci örnekteki kabul olasılığını saptamak için ikinci örnekteki kabul durumları listelemek
gerekir.İkinci bir örneklemeye yalnızca ilk örnekteki kusurlu sayısı 2 veya 3 ise gerek duyulur, yani
c1<d1≤c2 ise; d1=2 ve d2=0 veya 1 ise, yani ilk örnekten 2 ikinci örnekten 1 veya daha az kusurlu
bulduğumuz durumdur. Bu durumun olasılığı;
1.
d1=3 ve d2=0 ise, yani 3 kusurluyu da ilk örnekten bulduğumuz ve ikinci örnekten hiç kusurlu bulmadığımız
durumdur. Bu durumun olasılığı;
Dolayısıyla ikinci örnekten kabulün olasılığı;
Bu durumda kusurlu oranının p=0.005 olduğu bir partinin kabul olasılığı;
OC eğrisinin diğer noktaları da benzer şekilde hesaplanır.
Ortalama Örnekleme Sayısı Eğrisi (ASN-Average Sample Number)
Eğer ikinci örneklemenin tamamını denetlersek , ikili örneklemede ortalama örnekleme
sayısı için genel formül
P1 ilk örnekleme için partiyi kabul veya reddetme olasılıgıdır. Yani
P1= P{parityi ilk örnekleme de kabul etmek} + P { partiyi ilk örneklemede reddetmek}
Eğer denklem 14-7 deki kısmi parti bozuk ürünler p’ nin değişik değerleri için
değerlendirilirse , ASN- p grafiği ortalama örnekleme sayısı eğrisi olarak adlandırılır.
Azaltılmış ikili örnekleme planında ikinci örnekleme üzerinde ASN eğrisi formülü
Düzeltici Denetleme
İkili örnekleme ile düzeltici örnekleme yapıldığında , AOQ eğrisi
bütün bozuk ürünlerin örneklemede yada 100% denetlemede bulunduğu ve sağlamalarıyla
değiştirildiği kabul edildiğinde yukarıdaki şekilde elde edilir
‘in son parti kabul olasılığı olduğunu ve bu
kabul olasılığının parti veya sürecin kalite seviyesi p’ ye bağlı olduğunu
hatırlayın
Çoklu Örnekleme Planları
•
Çoklu örnekleme planı bir partiyi ret etmeden önce ikiden fazla örnekleme kullanarak
oluşturulur ve ikili örnekleme sisteminin bir uzantısıdır.
Bu plan şu şekilde çalışır: eğer herhangi bir aşamanın tamamlanması sırasında, bozuk
olan ürün sayısı kabul sayısından az veya eşitse, parti kabul edilir. Eğer denetimin
herhangi bir aşaması esnasında bozuk ürün sayısı red sayısını eşit olur veya aşarsa parti
reddedilir. Diğer zamanlarda bir sonraki örnekleme alınır. Çoklu örnekleme prosedürü
5 tane örnekleme alınıncaya kadar devam eder ki bu zamanda parti için bir karar
verilmesi gerekir. İlk örnekleme çoğunlukla 100% oranında denetlenir. Daha sonraki
örneklemlerin denetlenme oranı çoğunlukla azaltılır.
Sıralı Örnekleme Planı
Sıralı örnekleme ikili örnekleme ve çoklu örnekleme konseptlerinin bir uzantısıdır. Sıralı
örneklemede bir partiden sıralı örneklemeler alınır ve örnekleme işleminin sonucuna göre
örnekleme sayısı belirlenir. Pratikte, sıralı örnekleme teorik olarak sonsuza kadar devam edebilir,
ta ki partinin %100’i kontrol edilene kadar. Pratikte, sıralı örnekleme planları denetlenmiş ürün
sayısı tekli örnekleme modeliyle yapılacak denetleme sayısının üç katına ulaştığında biter. Eğer
secilen örnekleme sayısı her aşamada 1 ‘den büyük olursa süreç, grup sıralı örnekleme olarak
adlandırılır. Eğer her aşamada kullanılan örnekleme sayısı 1 olursa süreç parçadan-parçaya sıralı
örnekleme olarak adlandırılır.
Bu eşitliklerin kullanımını örneklemek istersek;
için varsayalım ki biz sıralı örnekleme planını bulmak istiyoruz.
Bu yüzden, limit
çizgileri
ve
Partiyle ne yapılacağına grafik ile karar vermek yerine, sıralı
örnekleme planı Tablo 14-3 teki gibi gösterilebilir. Tablodaki girdiler,
kabul ve ret çizgilerinde için kullanılan denklemlerde n’nin değerlerini
değiştirerek ve kabul ve ret sayılarını hesaplayarak bulunabilir. Örnek
olarak, n=45 için hesaplamalar:
Kabul ve red sayıları tamsayı olmak zorundadır, dolayısıyla kabul sayısı sonraki tamsayı XA’ya eşit veya daha
küçük ve red sayısı sonraki tamsayı XR’ye eşit veya daha büyüktür. Yani, n=45 için kabul sayısı 0 red sayısı
3’dür.Dikkat edelim ki parti 44’üncü birim test edilinceye kadar kabul edilmemektedir.Tablo 14-3’de sadece ilk 46
birim gösterilmiştir. Doğal olarak, plan 276 birimin, tekli örnekleme planı için gerekli örnek büyüklüğünün üç
katıdır, kontrolünden sonra durdurulur.
Sıralı Örnekleme için OC ve ASN Eğrileri
Sıralı örnekleme için OC eğrisi kolayca elde edilebilir. Eğri üstündeki iki
nokta(p1 ,1- α) ve (p2,β). Bir üçüncü nokta, eğrinin ortası civarında, p=s ve
Pa=h2/(h1+h2) .
Sıralı örneklemede alınan ortalama örnekleme sayısı
burada
ve
Düzeltici denetleme
Sıralı örneklemede ortalama çıktı kalitesi(AOQ) yaklaşık olarak şu şekilde
verilebilir
Ortalama toplam denetim de kolayca elde edilebilir. Dikkat edin; parti kabul
edildiğinde örnekleme sayısı A/C ve parti reddedildiğinde N olur. Bu yüzden
ortalama denetleme sayısı
Deney Tasarımı
ÖRNEK
Örnek-2
Örnek-1 Küçük iyidir.
Örnek-3