KGY ‘ları ile elde ettiğimiz denklemler lineer bağımsız bir denklem takımı
oluşturuyor mu?
9
8
1
7
3
2
4
2
5
3
1
6
5
4
Matrise dikkatle bakın !!!!
1
0
A
0
0
0
0
0
0
1
0 1 0
0
0
1
1
0
0
1
1
0
1
0
0
0
0 1 1
0
0
1
0
1
0
1
0
v1
1 0 0 0
v
1 0 0 0
2
v3
0 1 0 0
e
1
0
0
1
0
e v4
0 0 1 1 2 v5
e3
0 0 0 1 v6
0 1 1 0 e5 v
7
v8
1 1 0 0
1
0
1
0
v9
M
AT M
Teorem: (Tellegen Teoremi)
ne elemanlı bir G grafında i1
sağlayan bir küme,
küme olsun
v1
i2 ... ine i
T
KAY’sını
v2 ... vne v KGY’sını sağlayan bir
T
vT i 0
Tanıt: Referans düğümünü belirle ve A matrisini tanımla
Ai 0
T
A ev
T
T T
v i ( A e) i
eT ( AT )T i
eT Ai 0
Tellegen Teoremi ‘ne dikkat edersek:
v ve i birbirleriyle ilgili değil sadece G grafı için KGY ve KAY sağlamamları
Yeterli. G için v’ ve v’’ KGY, i’ ve i’’ KAY’yi sağlıyorsa
vT i 0
vT i 0
vT i 0
vT i 0
Tellegen Teoremi sadece devrenin topolojisine bağlıdır
Lineer bağımsız akım ve gerilim denklemlerini elde etmenin
başka yolu var mı?
KAY’sı ve KGY’sını başka nerede yazdık?
K1
K5
9
8
1
K6
7
3
2
KAY’den başlayalım
4
2
5
3
1
K3
6
K2
5
4
K7
K4
Burada aslında kaç tane lineer
bağımsız denklem var?
Bu sayı aynı zamanda neye eşit?
1
1
0
0
0
0
0
1
0
0
0
1 1
1
0
0
0
0
1
0
0
1 0
0
0
1
1
0 1
0
0
0
1 0
1
i1
0 0 1 1 i3 0
1 0 0 0 i4 0
1 0 0 0 i5 0
1 1 0 1 i2 0
0 1 0 1 i6 0
0 1 1 0 i7 0
1 0 1 1 i8 0
i
9
Qa
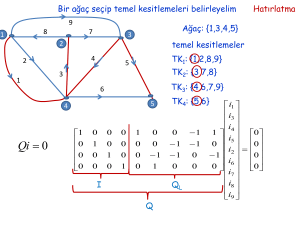
Bir ağaç seçip temel kesitlemeleri belirleyelim
9
8
1
7
Ağaç: {1,3,4,5}
3
temel kesitlemeler
2
4
2
1
TK1: {1,2,8,9}
5
TK2: {3,7,8}
3
TK3: {4,6,7,9}
6
4
Qi 0
1
0
0
0
5
TK4: {5,6}
0
0
0
1
0
0
1
1
0
0
0
0
1
1
0
1
0
0
1
1
0
0
0
1
0
1
0
0
I
QL
Q
i1
i
3
i4
1 0
i5 0
0
i2
1 0
i6
0 0
i
7
i8
i
9
Şimdi de KGY’sına bakalım
9
8
1
7
3
Çevreleri belirleyelim
2
4
2
5
3
1
6
5
4
1
0
0
0
0
1
1
1
0
0
0
1 0
1
1
0
1
0
0
0
0
0
1
0
0
0
0
1
0
1
0
0
1
Ç1 : {1,2}
Ç7 : {1,4,7,8}
Ç2 : {2,3,8}
Ç8 : {1,5,6,7,8}
Ç3 : {3,4,7}
Ç9 : {2,4,9}
Ç4 : {4,5,6}
Ç10 : {2,5,6,9}
Ç5 : {7,8,9} Ç : {2,5,6,9}
0
11
0
0
0
0
1
0 v1
Ç6 : {1,3,8}
1
0
0
1
0
0 v2 0
1 1 1
0
0
0 v3 0
0
0
0
1 1 1 v4 0
Burada aslında
0
0
0
0
1
0 v5 0
kaç tane lineer
1 0
0 1 1
0 v6 0
bağımsız denklem var?
0 1 1 1 1
0 v7 0
5
1 0
0
0
0 1 v8 0
0 1 1
0
0 1 v9
0
1 1 1
0
0
0
0
0
0
0
Şimdi de temel çevreleri belirleyelim
Ağaç: {1,3,4,5}
9
8
1
7
3
2
5
3
1
6
4
1
0
0
0
0
0
0
0
0
1 0
0
1
0
0
0
0
0
1
0
1
0
0
0
1
1
0
0
1
0
1
1
0
0
0
0
1
1 0
1
I
Bt
B
temel çevreler
Ç1 : {1,2}
4
2
5
v2
v
6 0
0 v7 0
1 v8 0
0 v9 0
0 v1 0
0 v3 0
v4 0
v
5
kirişler: {2,6,7,8,9}
Ç3 : {3,4,7}
Ç2 : {4,5,6} Ç4 : {1,3,8}
Ç5 : {1,4,9}
Bv 0
Teorem: Bir birleşik G’ında seçilen T ağacı için Q ve B sırasıyla temel
kesitleme ve temel çevre matrisi olsun
QB T 0
Tanıt:
QT vt v
Bv 0
BQT vt 0
Dallar: {1,3,4,5}
1 0 0 1 1
0 0 1 1 0
Q
0 1 1 0 1
0 0 0
0 1
Qi 0
1 0 0
0 1 0
0 0 1
0 0 0
Q vt v
T
vt
QB T 0
Kirişler: {2,6,7,8,9}
i2
i
6
i7
0 0
1
i
8
0
0 0
i9
0 0 B 0
i1
1 0
0
i3
0
i4
i5
0
0
0
0
1 0
0
1
0
0
0
0
0
1
0
1
0
0
0
1
1
0
0
1
0
1
1
0
0
0
0
1
1 0
1
Bv 0 BT il i
v2
v
6 0
0 v7 0
1 v8 0
0 v9 0
0 v1 0
0 v3 0
v4 0
v
5
KGY kapalı düğüm dizileri, düğüm gerilimleri cinsinden eleman gerilimleri,
çevreler için yazılıyor
KAY Gauss yüzeyleri, kesitlemeler, düğümler için yazılıyor
KAY’na ilişkin bağımsız denklem takımı nd -1 düğüm için yazılan denklemler
KAY’na ilişkin bağımsız denklem takımı temel kesitlemeler için
yazılan denklemler
KGY’na ilişkin bağımsız denklem takımı temel çevreler için
yazılan denklemler
Toplam Lineer Bağımsız Denklem Sayısı
Qi 0
nd -1 denklem
Bv 0
ne -nd +1 denklem
Toplam sayı
Bilinmiyen sayısı kaç?
2ne
ne
Eksik denklemleri nereden bulacağız?
1
2
3
1
4
2
3
5
6
4
7
5
9
8
6
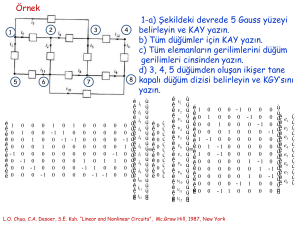
1-a) 4 düğümünü referans alıp A matrisini
yazınız.
b) 4 düğümü referans iken KGY’ye ilişkin
denklemleri yazınız.
c) {2,4,6,7,8} ağacına ilişkin temel çevre ve
temel kesitlemeleri belirleyiniz.
d) v2=2V, v4=4V, v6=6V, v7=7V, v8=8V ise
diğer elemanlara ilişkin gerilimleri
belirleyiniz.
e) i1=1A, i3=3A, i5=5A, i9=9A ise
diğer elemanlara ilişkin akımları
belirleyiniz.
f) Tellegen Teoreminin sağlandığını
gösteriniz.
Eleman Tanım Bağıntıları
f R (v, i, t ) 0
v
i
fC (v, q, t ) 0
q
i q
v
f m ( , q, t ) 0
memristor
endüktans
Kapasite
direnç
f L ( , i, t ) 0
Ø
Direnç Elemanı: v ve i arasında cebrik bağıntı ile temsil edilen eleman
Endüktans Elemanı: Ø ve i arasında cebrik bağıntı ile temsil edilen eleman
Kapasite Elemanı: v ve q arasında cebrik bağıntı ile temsil edilen eleman
Memristor Elemanı: Ø ve q arasında cebrik bağıntı ile temsil edilen eleman
2-Uçlu Direnç Elemanları
• lineer, lineer olmayan, zamanla değişen, değişmeyen, akım
ve/veya gerilim kontrollü dirençlerin tanım bağıntıları,
• seri, parallel bağlı dirençlere ilişkin uç bağıntıları,
• lineer olmayan dirençlere ilişkin dc (doğru akım) çalışma
noktasının belirlenmesi, küçük işaret analizi.
Lineer Direnç
+
()
v(t ) Ri (t )
direnç
i (t ) Gv(t )
iletkenlik, siemens
mho
v
v (t )
(S )
i (t )
v (t )
i (t )
i-v düzlemi
v-i düzlemi
Hatırlatma: Lineerlik
f ( x1 ) y1
f ( x2 ) y2
f (.) lineer
f (x1 x2 ) f ( x1 ) f ( x2 )
y1 y 2
Özel Lineer Dirençler:
Açık devre elemanı
f (i, v) i 0
v (t )
i (t )
R
G0
i (t )
i-v düzlemi
v (t )
v-i düzlemi
Kısa devre elemanı
f (i, v) v 0
v (t )
i (t )
R 0 i (t )
i-v düzlemi
G
v (t )
v-i düzlemi
Açık devre elemanı ve kısa devre elemanının i-v,v-i karakteristiklerine
dikkat edelim !!!
v (t )
i (t )
R
G0
i (t )
i-v düzlemi
v (t )
v-i düzlemi
Tanım: (Dual Dirençler)
A direncinin v-i karakteristiği B direncinin i-v karakteristiği ile aynıdır.
A direnci B direncinin dual’idir.
Lineer direnç elemanına ilişkin ani güç
Lineer Olmayan Direnç
+
v
_
f ( v, i ) 0
p(t ) v(t )i (t ) Ri 2 (t )
Bazı Özel Lineer Olmayan Dirençler
İdeal Diyot
+
v
_
RID {( v, i) : vi 0, i 0, v 0 ve v 0, i 0}
Diyot tıkamada
Diyot iletimde
(v 0),
(i 0),
i0
v0
v (t )
i (t )
i (t )
v (t )
i(t )
i-v düzlemi
v-i düzlemi
Diyot tıkamada iken davranışı hangi eleman gibi?
Is
v(t )
Diyot iletimde iken davranışı hangi eleman gibi?
p-n Jonksiyon Diyodu (alçak frekanslardaki özellikleri)
+
v
_
uç büyüklükleri
v
RD {( v, i ) : i I s [exp( ) 1], I s , vT sabit }
vT
q elektron yükü
kT
I s ters doyma akımı VT
k Boltzman sabiti
q
T Sıcaklık (Kelvin)
VT 0,026V
Tünel Diyod
+
RTD {( v, i ) : i iˆ(v)}
v
i (t )
İ1
v1 v v2 eğim negatif
_
osilatör, kuvvetlendirici
İ2
İ 2 i İ1 her akıma
üç gerilim karşılık düşüyor
hafıza, anahtarlama
V1 V2
gerilim kontrollü, akım kontrollü değil
Bağımsız kaynaklar
Bağımsız gerilim kaynağı
+
+
vs (t ) vs (t )
_
_
v(t )
Rvs {( v, i) : v vs (t ), i }
i (t )
v (t )
Bağımsız gerilim kaynağı lineer eleman mı?
Bağımsız gerilim kaynağı gerilim kontrollü mü?
Bağımsız gerilim kaynağı akım kontrollü mü?
vs (t ) 3V
Bağımsız akım kaynağı
+
is (t )
v
Ris {( v, i) : i is (t ), v }
_
Zamanla Değişen Dirençler
v-i karakteristiği zamanla değişen dirence zamanla değişen direnç denir.
Lineer Zamanla Değişen Direnç
+
v
v(t ) R(t )i (t )
v (t )
R (t )
i (t ) G (t )v(t )
i (t )
_
t
Anahtar
i
+
v
_
S(t)
t
S(t)
v
i
+
+
v
_
Seri ve Paralel 2-uçlu Direnç Elemanlarının
Oluşturduğu 1-Kapılılar
i
N
1-kapılısı
i kapı akımı
v kapı gerilimi
1-kapılının özellikleri
kapı akımı ve gerilimi
cinsinden yazılır
Seri bağlı 2-uçlu dirençler
i d1
i1
+
+
R1
v1
v
d2
R2
N
_
d3
_
i
+2
v2
_
+
N
1-kapılısı
v
_
Tanım Bağıntıları
v1 vˆ1 (i1 )
KAY
v2 vˆ2 (i2 )
KGY
i i1
1. düğüm
1-2-3-1 düğüm dizisi
i1 i2
2. düğüm
v1 v2 v 0
v1 v2 v
Amaç:
v vˆ(i ) bağıntısını bulmak
KGY
+
KAY
v v1 v2
v vˆ1 (i ) vˆ2 (i ) ˆ vˆ(i )
i
+
R1
i1
+
v1
_
_
v
R2
N
Sonuç:
_
v vˆ1 (i) vˆ2 (i)
v2
+
i2
KAY
tüm elemanların akımı kapı akımı ile aynı
KGY
kapı gerilimi eleman gerilimlerinin toplamı
elemanlar akım kontrollü elde edilen 1-kapılı da akım kontrollü
Bir soru: İki uçlunun tanım bağıntısını elde ediniz
Bir başka soru:
Bu iki uçlunun da tanım bağıntısını elde ediniz
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”, Mc.Graw Hill, 1987, New York