Elektrik Devrelerinin Temelleri

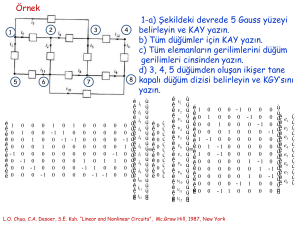
3. Kirchhoff’un Akım Yasası (KAY)
Tüm toplu parametreli devrelerde, her t anında herhangi bir kesitlemeye
ilişkin akımların cebirsel toplamı sıfırdır.
Teorem:
Gauss Yüzeyleri için
KAY
Tanıt: (1)
Düğümler için
KAY
(2)
Gauss yüzeylerini düğümleri içerecek şekilde seç
(2)
(3)
(3)
(1)
Kesitlemeler için
KAY
Düğümler için KAY
Her kesitleme düğümleri iki gruba ayırıyor.
Gruplardaki her düğüm için yazılan KAY’ları toplanırsa
kesitleme için yazılan denklem elde edilir.
Her kesitlemeye ilişkin yazılan KAY’sına ilişkin denklem
kesitlemeye karşı düşen Gauss yüzeyine ilişkin yazılan
KAY’sına ilişkin denkleme denk gelmektedir .
nd düğümlü bir grafta nd düğüm için yazılan KAY ‘sına ilişkin denklemler
lineer bağımsız bir denklem takımı oluşturur mu?
Hatırlatma
Lineer Bağımsız Denklem Takımı
fi ( x1, x2 ,..., xn )  i1 x1  i2 x2  i3 x3  ....  in xn  0
i  1,...m
n bilinmiyenli ........denklemin
m
f i (.) ‘lerin belirlediği ......
lineer bağımsız bir
denklem takımı oluşturduğunu nasıl anlarız?
m
 ki fi ( x1, x2 ,..., xn )  0
i 1
x1 , x2 ,..., xniçin sağlayan sıfırdan farklı ki‘ler varsa bu
lineer bağımlıdır.
denklem takımı ...................................
bazı denklemler diğerleri cinsindenifade
m denklem lineer bağımlı ise .................................................................
edilebilir.
Örnek: f ( x
1
1 , x2 , x3 , x4 )
 x1  x2  x3  3x4  0
Lineer bağımsızlar mı?
f1 ( x1 , x2 , x3 , x4 )  2 x1  3x2  x3  4 x4  0
f1 ( x1 , x2 , x3 , x4 )  4 x1  11x2  5 x3  18 x4  0
nd düğümlü bir grafta nd düğüm için yazılan KAY ‘sına ilişkin denklemler
lineer bağımsız bir denklem takımı oluşturur mu?
1
3

aik   1
5
0

9
8
1
7
2
4
2
1
3
6
4
9 bilinmiyenli
5 denklem
var.
1.d  1
2.d  0
1
0
0 1

3.d  0
0 0

4.d  1  1 1
0 0
5.d  0
Boyutu ne?
k. elemanın akımı i. düğümden
dışarı ise
k. elemanın akımı i. düğüme
doğru ise
k. eleman i. düğüme bağlı değil
ise
 i1 
i 
5
 2
0 0 0 0  1 1  i3  0
 
0 0 0 1 1 0  i4  0
1 1 0  1 0  1 i5   0
   
 1 0 1 0 0 0  i6  0
0  1  1 0 0 0  i7  0
 
i8 
i  Ø
 9
Aa
i
...... bilinmiyenli ........denklem var ise lineer bağımsız bir denklem takımı
oluşturup oluşturmadıklarını nasıl anlarız?
rankı inceleriz sıfır satır oluşturacak şekilde satır/sütun işlemleri yaparız
Aa ‘nın rankı kaç?
2.d  0
3.d  0
0
0

4.d  1  1

5.d  0
0
1
0
0
0
1
0
1
1
0
1 0
1
1
0
1
0
0
0
0
1 1
0
0
Boyutu ne?
Rankı ne?
A
1
 i1 
i 
 2
i3  0
0    
i4  0


 
 1
i5   0
0    
 i6  0
0  
0
i7
 
i8 
i 
 9
1.d 1
0
2.d 
3.d 0

5.d 0
 i1 
i 
 2
i3  0
1 0 0 0 0 0 1 1    
i4  0


 
0 1 0 0 0 1 1 0 
i5   0
0 0 1 1 0  1 0  1    
 i6  0
0 0 0 1 1 0 0 0  
0
i7
 
i8 
Boyutu ne? A
i 
 9
Rankı ne?
İndirgenmiş düğüm matrisi A
Ai=0
Teorem: nd düğümlü birleşik bir grafta nd-1 düğüm için yazılan KAY’ları
lineer bağımsız bir denklem takımı oluşturur.
Tanıt: nd -1 tane denklemden k tanesi lineer bağımlı olsun:
k
  i fi (i1, i2 ,..., ine )  0
i 1
i1 , i2 ,..., ine
 i  0, i  1,2,..., k
Birleşik graf
k düğüm ve nd –k düğümü ayrı iki grup olarak
düşünelim. Bu düğüm gruplarını birleştiren bir
graf elemanı mutlaka vardır.
Bu graf elemanına ilişkin akım k denklemde sadece bir defa
gözükecektir.
Yazılan k denklemde bu akım diğer akımlar cinsinden ifade
edilemez.
k denklem lineer bağımlı olamaz.
nd-1 denklem lineer bağımlı olamaz.
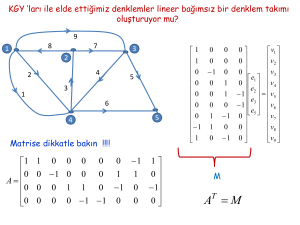
KGY ‘ları ile elde ettiğimiz denklemler lineer bağımsız bir denklem takımı
oluşturuyor mu?
9
8
1
7
3
2
4
2
5
3
1
6
5
4
Matrise dikkatle bakın !!!!
1
0
A
0

0
0
0
0
0
1
0 1 0
0
0
1
1
0
0
1
1
0
1
0
0
0
0 1 1
0
0
1
0
1
0 
 1

0
 v1 
1 0 0 0
v 
1 0 0 0
 2


v3 
 0 1 0 0 

  e1   
 0 0 1 0   e   v4 
 0 0 1  1  2   v5 

 e3   
 0 0 0  1   v6 
 0 1  1 0  e4  v 
 7


v8 
 1 1 0 0 
v 
 1 0 1 0 


 9
M
AT  M
Teorem: (Tellegen Teoremi)
ne elemanlı bir G grafında i1

sağlayan bir küme,
küme olsun
v1
i2 ... ine   i
T
KAY’sını
v2 ... vne   v KGY’sını sağlayan bir
T
vT i  0
Tanıt: Referans düğümünü belirle ve A matrisini tanımla
Ai  0
T
A ev
T
T T
v i  ( A e) i
 eT ( AT )T i
 eT Ai  0
Tellegen Teoremi ‘ne dikkat edersek:
v ve i birbirleriyle ilgili değil sadece G grafı için KGY ve KAY sağlamamları
Yeterli. G için v’ ve v’’ KGY, i’ ve i’’ KAY’yi sağlıyorsa
vT i  0
vT i  0
vT i  0
vT i  0
Tellegen Teoremi sadece devrenin topolojisine bağlıdır
Lineer bağımsız akım ve gerilim denklemlerini elde etmenin
başka yolu var mı?
KAY’sı ve KGY’sını başka nerede yazdık?
K1
K5
9
8
1
K6
7
3
2
KAY’den başlayalım
4
2
5
3
1
K3
6
K2
5
4
K7
K4
Burada aslında kaç tane lineer
bağımsız denklem var?
Bu sayı aynı zamanda neye eşit?
1
1

0

0
0

0
0

1
0
0
0
1 1
1
0
0
0
0
1
0
0
1 0
0
0
1
1
0 1
0
0
0
1 0
1
 i1 
0 0  1 1  i3  0
 1 0 0 0  i4  0
 
1 0 0 0  i5  0

 
1 1 0 1  i2   0
 
0  1 0  1 i6  0

 
0 1 1 0  i7  0
 

1 0  1 1  i8  0
i 
 9
Qa
Bir ağaç seçip temel kesitlemeleri belirleyelim
9
8
1
7
Ağaç: {1,3,4,5}
3
temel kesitlemeler
2
4
2
1
TK1: {1,2,8,9}
5
TK2: {3,7,8}
3
TK3: {4,6,7,9}
6
4
Qi  0
1
0

0

0
5
TK4: {5,6}
0
0
0
1
0
0
1
1
0
0
0
0
1
1
0
1
0
0
1
1
0
0
0
1
0
1
0
0
I
QL
Q
 i1 
i 
 3
i4 
1    0 
i5  0
0
 i2    
 1   0
 i6   
0    0 
i
 7
i8 
i 
 9
Şimdi de KGY’sına bakalım
9
8
1
7
3
Çevreleri belirleyelim
2
4
2
5
3
1
6
5
4
1
0

0

0
0

1
1

1
0

0

0
1 0
1
1
0
1
0
0
0
0
0
1
0
0
0
0
1
0
1
0
0
1
Ç1 : {1,2}
Ç7 : {1,4,7,8}
Ç2 : {2,3,8}
Ç8 : {1,5,6,7,8}
Ç3 : {3,4,7}
Ç9 : {2,4,9}
Ç4 : {4,5,6}
Ç10 : {2,5,6,9}
Ç5 : {7,8,9} Ç : {2,5,6,9}
0
11
0
0
0
0
1
0   v1 
Ç6 : {1,3,8}
1
0
0
1
0
0  v2  0

1 1 1
0
0
0  v3  0
 
0
0
0
1  1  1 v4  0
Burada aslında

 


0
0
0
0
1
0  v5  0
kaç tane lineer
 

1 0
0 1 1
0 v6  0
bağımsız denklem var?



0 1 1 1 1
0  v7  0
 

1 0
0
0
0  1 v8  0

0 1 1
0
0  1 v9 

0
1 1 1
0
0
0
0
0
0
0
Şimdi de temel çevreleri belirleyelim
Ağaç: {1,3,4,5}
9
8
1
7
3
2
5
3
1
6
4
1
0

0

0
0
0
0
0
0
1 0
0
1
0
0
0
0
0
1
0
1
0
0
0
1
1
0
0
1
0
1
1
0
0
0
0
1
1 0
1
I
Bt
B
temel çevreler
Ç1 : {1,2}
4
2
5
 v2 
v 
 6  0 
0  v7  0
 
 1  v8  0
 
0  v9   0
 
0   v1  0
 
0   v3  0
 
v4  0
v 
 5
kirişler: {2,6,7,8,9}
Ç3 : {3,4,7}
Ç2 : {4,5,6} Ç4 : {1,3,8}
Ç5 : {1,4,9}
Bv  0
Dallar: {1,3,4,5}
1
0
Q
0

0
0
0
0
1
0
0
1
1
0
0
0
0
1
1
0
1
0
0
1
1
0
0
0
1
0
1
0
0
Qi  0 QT vt  v
1
0

B  0

0
0
 i1 
i 
 3
i4 
1    0 
i5  0
0
 i2    
 1   0
 i6   
0    0 
i
 7
i8 
i 
 9
Kirişler: {2,6,7,8,9}
0
0
0
0
1 0
0
1
0
0
0
0
0
1
0
1
0
0
0
1
1
0
0
1
0
1
1
0
0
0
0
1
1 0
1
Bv  0 BT il  i
v2 
v 
 6  0 
0  v7  0
 
 1  v8  0
 
0  v9   0
   
0   v1 
0





0  v3
0
   
v4  0
v 
 5
Toplam Lineer Bağımsız Denklem Sayısı
Qi  0
nd -1 denklem
Bv  0
ne -nd +1 denklem
Toplam sayı
Bilinmiyen sayısı kaç?
2ne
ne
Eksik denklemleri nereden bulacağız?
Teorem: Bir birleşik G’ında seçilen T ağacı için Q ve B sırasıyla temel
kesitleme ve temel çevre matrisi olsun
QB T  0
Tanıt:
QT vt  v
Bv  0
BQ vt  0
T
vt
QB T  0
KGY kapalı düğüm dizileri, düğüm gerilimleri cinsinden eleman gerilimleri,
çevreler için yazılıyor
KAY Gauss yüzeyleri, kesitlemeler, düğümler için yazılıyor
KAY’na ilişkin bağımsız denklem takımı nd -1 düğüm için yazılan denklemler
KAY’na ilişkin bağımsız denklem takımı temel kesitlemeler için
yazılan denklemler
KGY’na ilişkin bağımsız denklem takımı temel çevreler için
yazılan denklemler