Ders Planı - AKTS Kredileri - Trakya Üniversitesi

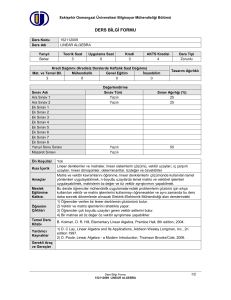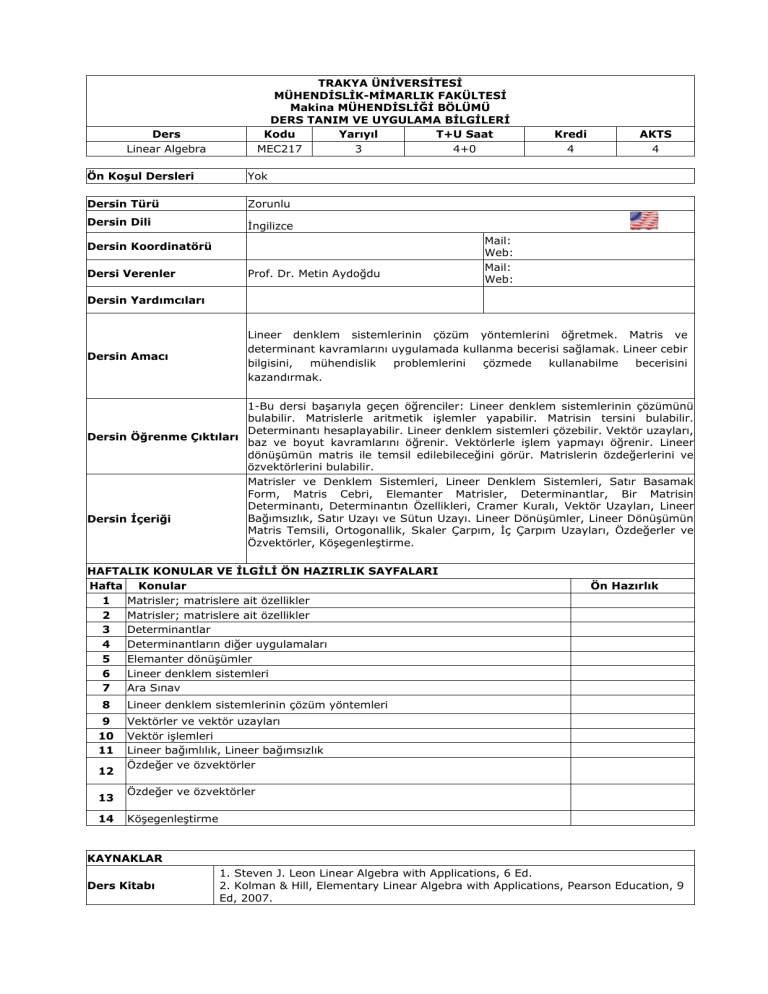
TRAKYA ÜNİVERSİTESİ
MÜHENDİSLİK-MİMARLIK FAKÜLTESİ
Makina MÜHENDİSLİĞİ BÖLÜMÜ
DERS TANIM VE UYGULAMA BİLGİLERİ
Kodu
Yarıyıl
T+U Saat
MEC217
3
4+0
Ders
Linear Algebra
Ön Koşul Dersleri
Yok
Dersin Türü
Zorunlu
Dersin Dili
İngilizce
Dersin Koordinatörü
Dersi Verenler
Prof. Dr. Metin Aydoğdu
Kredi
4
AKTS
4
Mail:
Web:
Mail:
Web:
Dersin Yardımcıları
Dersin Amacı
Lineer denklem sistemlerinin çözüm yöntemlerini öğretmek. Matris ve
determinant kavramlarını uygulamada kullanma becerisi sağlamak. Lineer cebir
bilgisini,
mühendislik
problemlerini
çözmede
kullanabilme
becerisini
kazandırmak.
1-Bu dersi başarıyla geçen öğrenciler: Lineer denklem sistemlerinin çözümünü
bulabilir. Matrislerle aritmetik işlemler yapabilir. Matrisin tersini bulabilir.
Determinantı hesaplayabilir. Lineer denklem sistemleri çözebilir. Vektör uzayları,
Dersin Öğrenme Çıktıları
baz ve boyut kavramlarını öğrenir. Vektörlerle işlem yapmayı öğrenir. Lineer
dönüşümün matris ile temsil edilebileceğini görür. Matrislerin özdeğerlerini ve
özvektörlerini bulabilir.
Matrisler ve Denklem Sistemleri, Lineer Denklem Sistemleri, Satır Basamak
Form, Matris Cebri, Elemanter Matrisler, Determinantlar, Bir Matrisin
Determinantı, Determinantın Özellikleri, Cramer Kuralı, Vektör Uzayları, Lineer
Bağımsızlık, Satır Uzayı ve Sütun Uzayı. Lineer Dönüşümler, Lineer Dönüşümün
Dersin İçeriği
Matris Temsili, Ortogonallik, Skaler Çarpım, İç Çarpım Uzayları, Özdeğerler ve
Özvektörler, Köşegenleştirme.
HAFTALIK KONULAR VE İLGİLİ ÖN HAZIRLIK SAYFALARI
Hafta Konular
1
Matrisler; matrislere ait özellikler
2
Matrisler; matrislere ait özellikler
3
Determinantlar
4
Determinantların diğer uygulamaları
5
Elemanter dönüşümler
6
Lineer denklem sistemleri
7
Ara Sınav
8
9
10
11
12
13
14
Ön Hazırlık
Lineer denklem sistemlerinin çözüm yöntemleri
Vektörler ve vektör uzayları
Vektör işlemleri
Lineer bağımlılık, Lineer bağımsızlık
Özdeğer ve özvektörler
Özdeğer ve özvektörler
Köşegenleştirme
KAYNAKLAR
Ders Kitabı
1. Steven J. Leon Linear Algebra with Applications, 6 Ed.
2. Kolman & Hill, Elementary Linear Algebra with Applications, Pearson Education, 9
Ed, 2007.
MATERYAL PAYLAŞIMI
Dokümanlar
Ödevler
Sınavlar
DEĞERLENDİRME SİSTEMİ
YARIYIL İÇİ ÇALIŞMALARI
SAYISI
KATKI YÜZDESİ
Ara Sınav
2
60
Ödev
4
40
Toplam
6
100
Yıl İçinin Başarıya Oranı
1
50
Finalin Başarıya Oranı
1
50
Toplam
100
Ders Kategorisi
Destek Dersleri
Temel Mesleki Dersler
x
Uzmanlık / Alan Dersleri
Beşerî, İletişim ve Yönetim Becerileri Dersleri
Aktarılabilir Beceri Dersleri
DERSİN ÖĞRENİM ÇIKTILARININ PROGRAM YETERLİLİKLERİ İLE İLİŞKİSİ
No Program Yeterlilikleri
Katkı Düzeyi
1
2
1 Matematik, fen ve mühendislik bilgilerini uygulama becerisi
3
Deney tasarımlama ve yapma ile deney sonuçlarını analiz etme ve yorumlama
becerisi
İstenen gereksinimleri karşılayacak biçimde bir sistemi, parçayı ya da süreci
3
tasarımlama becerisi
2
x
x
4 Disiplinler arası takımlarda çalışabilme becerisi
x
5 Mühendislik problemlerini tanımlama, formüle etme ve çözme becerisi
x
6 Mesleki ve etik sorumluluk bilinci
7
Mühendislik çözümlerinin, evrensel ve toplumsal boyutlarda etkilerini anlamak için
gerekli genişlikte eğitim
8 Yaşam boyu öğrenmenin gerekliliği bilinci
Mühendislik uygulamaları için gerekli olan teknikleri, yetenekleri ve modern araçları
kullanma becerisi
Mesleki gelişim açısından İngilizce dilinde literatür kullanmak ve izlemelerini
10
sağlamak
9
11 Matematik, fen ve mühendislik bilgilerini uygulama becerisi
Yeterliği Sağlama Düzeyi:
1 Düşük
2 Düşük – Orta
3 Orta
4 Yüksek
5 Mükemmel
4
x
x
x
x
x
x
x
5
AKTS(ECTS) / İŞ YÜKÜ TABLOSU
SAYISI
Süresi
(Saat)
Toplam İş
Yükü(Saat)
Ders Süresi
14
4
56
Sınıf Dışı Ders Çalışma Süresi(Ön çalışma, pekiştirme)
14
4
56
Ödevler
4
2
8
Ara sınavlar
2
2
4
Yarıyıl Sonu Sınavı
1
2
2
Etkinlik
Toplam İş Yükü(Saat)
126
Toplam İş Yükü(Saat)/ 30 (s)
4.2
Dersin AKTS Kredisi
4
ÖLÇME ve DEĞERLENDİRME YÖNTEMİ:
Trakya Üniversitesi Ön Lisans /Lisans Eğitim Öğretim ve Sınav Yönetmeliğine Maddesine göre öğrencinin
başarı notu bağıl değerlendirme yöntemi ile belirlenir.