Bölüm 4: Sayısal İntegral

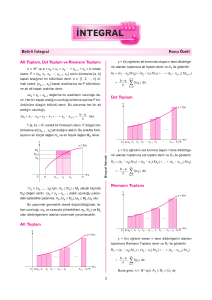
Bölüm 4: Sayısal İntegral
Bir f(x) fonksiyonunun tanımlı olduğu bir [a,b] aralığındaki belirli
aşağıdaki gibi tanımlanır;
b
S   f ( x)dx
a
S, [a,b] aralığında f(x) eğrisi ile x-ekseni arasındaki kalan yüzeyin
alanıdır.
f(x)
f(x)
a
b
x
Şekil 4.1: Sayısal integral şematik gösterimi
f(x)
f(b)
f(a)
a
b
x
Şekil 4.2: Sayısal integralde Trapez yöntemi şematik gösterimi.
Şekilde [a,b] aralığında eşit aralıklarla N sayıda nokta belirlersek, adım
uzunluğu aşağıdaki gibi olur;
(b  a)
h
N
a ve b noktalarını da katarak bo noktaları şöyle adlandırabiliriz.
x0=a, xi=a+ih, xN=b
(i=1,2,3,….,N-1)
Şekil 4.2 ‘deki integralin değeri herbir [xi, xi+1] alt aralıklarındaki integral
değerlerinin toplamı olacaktır.
S
x1
x2
xN
x0
x1
x N 1
 f ( x)dx   f ( x)dx  ...........   f ( x)dx
S  s1  s2  s3  ..........  sN
Trapez Kuralı:
Trapez kuralı kapalı integral formüllerinin ilki olup, aşağıdaki eşitlikteki
polinomun birinci dereceden olduğu duruma karşılık gelir:
b
b
a
a
I   f ( x)dx   f1 ( x)dx
Şekil 4.5’i dikkate aldığığımızda, eğer h adımı çok küçükse, en basit
yaklaşıklıkla, her bir aralıkta fonksiyonu bir doğru parçası olarak alırız. Bu
durumda, [xi, xi+1] aralığında oluşan yamuğun alanı hesaplanabilir:
si 
( f i  f i 1 )
h
2
Burada fi sol kenar, fi+1 sağ kenar ve h genişliktir.
f(x)
f(x)
h
.........
x0=a x1 x2 x3 . . . .
xn=b
x
Şekil 4.3.
N tane yamuk alanı toplanırsa, sayısal integral için trapez formülü
bulunmuş olur.(Şekil4.3.)
S
b

a
( f 0  f1 )
( f  fN )
( f  f2 )
h 1
h  ...........  N 1
h
2
2
2
1

f ( x)dx  h  f 0  f1  f 2  f 2  ...........  f N 1  f N   O(h 2 ) Trapez Formülü
2

Simpson Formülü:
Trapez formülüne göre daha iyi bir yaklaşımla, N sayıda çift alınır ve
ardışık iki alt aralık birlikte ele alınırsa;
S
S
elde edilir.
x1
x2
xN
x0
x1
x N 1
x2
x4
xN
x0
x2
x N 2
 f ( x)dx   f ( x)dx  ...........   f ( x)dx
 f ( x)dx   f ( x)dx  ...........   f ( x)dx
(*)
S  s1  s3  s5  ..........  sN 1
Trapez kuralını daha sık aralıkla uygulamaktan başka, integrali daha
doğru hesaplamak için diğer bir yol, noktaları birleştirmek için daha
yüksek dereceli polinomlar kullanmaktır. Örneğin, eğer f(a) ve f(b)
noktaları arasında bilinen ek bir nokta varsa(Şekil5.3), bu üç nokta bir
parabolle birleştirilebilir. Eğer f(a) ve f(b) arasında eşit aralıklı iki nokta
varsa, bu dört nokta üçüncü dereceden bir polinom ile birleştirilebilir. Bu
polinomlar altında kalan integralleri veren formüller Simpson Kuralları diye
adlandırılır.
f(x)
f(x)
f(b)
f(a)
parabol
a=xi-1
xi
b=xi+1
x
Şekil 4.4:Sayısal İntegralde Simpson yaklaşımı grafiği.
Şekildeki parabol denklemi;
f ( x) 
( x  xi )( x  xi 1 )
( x  xi 1 )( x  xi 1 )
( x  xi 1 )( x  xi )
f i 1 
fi 
f i 1
( xi 1  xi )( xi 1  xi 1 )
( xi  xi 1 )( xi  xi 1 )
( xi 1  xi 1 )( xi 1  xi )
Bu ifade (*) denkleminde yerine konur ve si integrali analitik olarak
alınırsa;
si 
xi1

xi 1
f ( x)dx 
h
 fi 1  4 fi  fi 1 
3
olur.
si ifadeleri S integralinde yerine konursa;
S
h
 f 0  4 f1  f 2   h  f 2  4 f 3  f 4   h  f 4  4 f 5  f 6   ........  h  f N 2  4 f N 1  f N 
3
3
3
3
b

a
f ( x)dx 
h
 f 0  4 f1  2 f 2  4 f3  2 f 4  .........  4 f N 1  f N   O(h 4 )
3
olarak Simpson Formülü elde edilir.
Gauss Integrali:
Tüm integral yöntemlerinde sayısal integral aşağıdaki şekilde alınır.
b
N
 f ( x)dx   w f ( x )
a
i 1
i
i
Trapez ve Simpson yöntemlerinde 100 veya 200 nokta kullanılarak
bulunan sonuçlar aynı duyarlıkta, 3 veya 5 nokta kullanılarak Gauss
yöntemiyle elde edilebilir.
Trapez ve Simpson yöntemlerinde xi noktaları eşit aralıklarla sıralanıyor
ve bunlar ağırlık katsayıları 2,4,4,….gibi sabit değerler alıyordu.
Gauss yönteminde eşit aralıkta noktalar kullanmak yerine, daha az
sayıda nokta kullanılır ve bunların katsayıları farklı alınır.
•f(x) fonksiyonunun [-1,1] aralığındaki integralini N=2 noktanın toplamı
olarak yazalım:
1
 f ( x)dx  w f ( x )  w
1
1
1
x1, x2, w1 ve w2 bilinmeyen parametreler.
2
f ( x2 )
1
 1dx  2  w  w
f (x)  1 
1
2
(1)
1
1
f ( x)  x 
 xdx  0  w x
1 1
 w2 x2
1
1
2
 x dx  3  w x
2
f ( x)  x 
2
2
1 1
 w2 x22
(2)
(3)
1
1
f ( x)  x 
3
 x dx  0  w x
3
1
3
1 1
 w2 x23
(4)
(2) Denklemini x12 çarpıp dördüncüden çıkarırsak;
w2 x2 ( x2  x1 )( x2  x1 )  0
Bu eşitliği sağlamak üç şekilde mümkündür.
Ya x2=0, veya x1=x2, yada x1=-x2 olmalıdır. İlk iki ifade anlamsızdır,
çünkü formül tek noktaya inmiş olur.
Bu durumda x1=-x2 alıp diğer bilinmeyenleri bulursak,
(2) denkleminden;
w1x1+w2x2=0
w1x1=-w2x2
(x1=-x2 alınırsa)
w1(-x2)=-w2x2
w1=w2
(1)’den
w1+w2=2
w1=w2=1 elde edilir.
(3)’den
w1x12+w2x22=2/3
w1=w2=1
x12+x22=2/3
x1=-x2 olduğundan,
x12+x12=2/3
x1=-x2=0.57735
Böylece, 2-noktalı Gauss integral formülünü şöyle yazabiliriz;
1
 f ( x)dx  f (0.57735)  f (0.57735)
1
Gauss yöntemi ikiden fazla nokta için genişletilebilir.
N sayıda nokta için,
1
N
 f ( x)dx   w f ( x )
i 1
1
i
i
Alıp, yine bu ifadenin x2N-1 dereceye kadar olan polinomlar için tam sonuç
vermesini isteyerek katsayılar hesaplanır. Gauss integrali için gerekli xi ve
wi değerleri ilk birkaç N sayısı için aşağıdaki tabloda verilmiştir.
Gauss yöntemini [-1,1] aralığında elde ettikten sonra, diğer [a,b] aralıkları
için de uygulanabilir. Bunu için lineer bir değişken dönüşümü yapılır:
u
(b  a) x  (b  a)
2
b

a
du 
ba
dx
2
alınırsa,
ba
 (b  a) x  (b  a) 
f (u )du 
f
dx



2 1 
2

1
elde edilir.
Tekil İntegraller:
Buraya kadar incelediğimiz integrallerde, açıkça belirtilmese de, sonlu bir
[a,b] aralığı ve bu aralıkta ıraksak olmayan bir f(x) fonksiyonu olduğu
varsayılmıştı. Uygulamada bu iki koşula uymayan birçok durumla
karşılaşılabilir. Örneğin;

I   f ( x)dx
0
0,  aralığı sonsuzdur, bu aralığı bilgisayarda
yoktur.
1
I 
0
(b  a )
N
aralığına bölme olanağı
1
dx
x
Bu integralde ise x=0 noktasında ıraksak olmaktadır. Sayısal integral
alındığında f(0) noktasında “sıfıra bölme” hatası verecektir.
Sonsuz aralığı sonlu hale getirmede ve ıraksaklığı ortadan kaldırmakta en
geçerli yöntem “değişken değişimi” yapmaktır.
Sınırları sonsuzda integraller: Bir integralin alt, üst veya her iki sınırı
sonsuzda ise, değişken değişimi yapılarak sınırlar sonlu hale getirilir.

I 
1
1
dx
x4
Yukarıdaki integral için değişken değişimi yapılırsa;
1
1 ve
du   2 dx
u
x
x

0
0
du  u 2 dx
1
1
I   4 dx   u 4 (u 2 )du   u 2 du   u 2 du
x
1
1
1
0
Bu durumda bilinen sayısal yöntemlerle integral alınabilir.
Sınırda ıraksak integraller: Eğer ıraksaklık görünürde ise, yine değişken değişimi
yöntemi kaldırılabilir;
1
Cosx
dx
x
0
I 
Bu integral sınırda ıraksaktır, bunun için x=u2, dx=2udu
yapılırsa;
1
1
1
Cosx
Cos(u 2 )
I 
dx  
2udu  2 Cos(u 2 )du
u
x
0
0
0
değişken değişimi
Nasıl bir değişken değişimi yapılacağının genel bir kuralı yoktur, her probleme
göre farklı düşünülmelidir.