integral - Google Groups

ÝNTEGRAL
Belirli Ýntegral
Konu Özeti
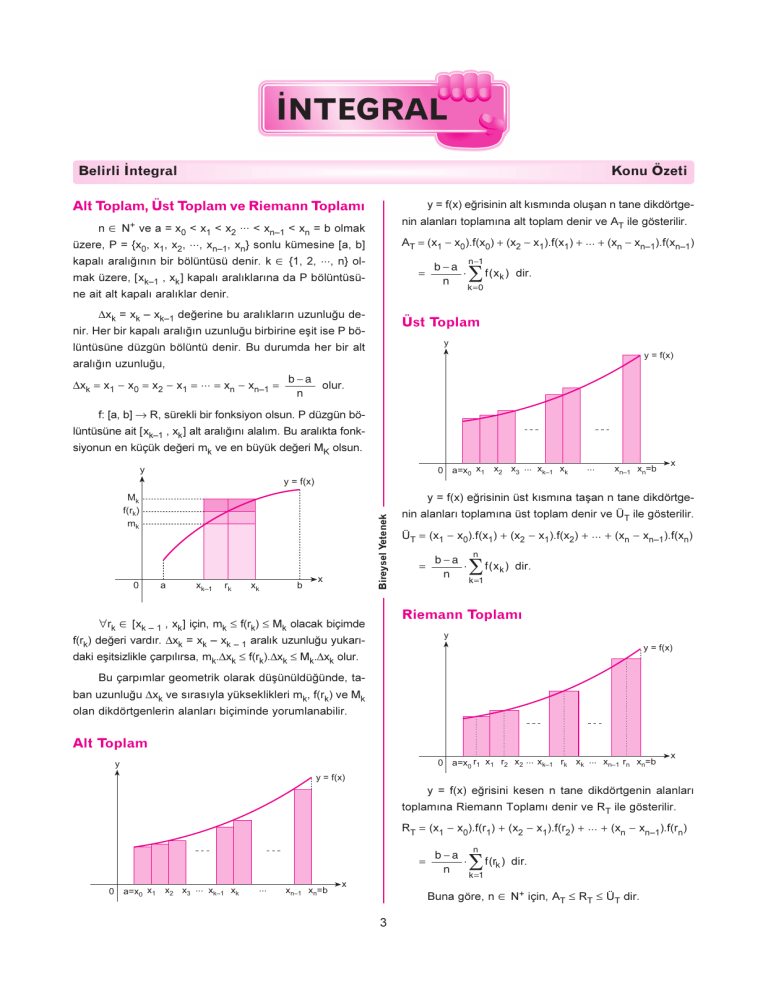
y = f(x) eğrisinin alt kısmında oluşan n tane dikdörtge-
Alt Toplam, Üst Toplam ve Riemann Toplamý
nin alanları toplamına alt toplam denir ve AT ile gösterilir.
n  N+ ve a = x0 < x1 < x2 ... < xn–1 < xn = b olmak
üzere, P = {x0, x1, x2, ..., xn–1, xn} sonlu kümesine [a, b]
kapalı aralığının bir bölüntüsü denir. k  {1, 2, ..., n} ol-
AT  (x1  x0).f(x0)  (x2  x1).f(x1)  ...  (xn  xn–1).f(xn–1)
AT 
mak üzere, [xk–1 , xk ] kapalı aralıklarına da P bölüntüsü-
ba

n
ne ait alt kapalı aralıklar denir.
xk = xk – xk–1 değerine bu aralıkların uzunluğu de-
n 1
 f(xk )
dir.
k 0
Üst Toplam
nir. Her bir kapalı aralığın uzunluğu birbirine eşit ise P bö-
y
lüntüsüne düzgün bölüntü denir. Bu durumda her bir alt
y = f(x)
aralığın uzunluğu,
ba
olur.
xk  x1  x0  x2  x1  ...  xn  xn–1 
n
f: [a, b]  R, sürekli bir fonksiyon olsun. P düzgün bölüntüsüne ait [xk–1 , xk ] alt aralığını alalım. Bu aralıkta fonksiyonun en küçük değeri mk ve en büyük değeri MK olsun.
0 a=x0 x1 x2 x3 ... xk–1 xk
y
y = f(x)
Mk
f(rk)
mk
xn–1 xn=b
x
y = f(x) eğrisinin üst kısmına taşan n tane dikdörtge-
a
xk–1
rk
xk
b
Bireysel Yetenek
0
...
x
nin alanları toplamına üst toplam denir ve ÜT ile gösterilir.
ÜT  (x1  x0).f(x1)  (x2  x1).f(x2)  ...  (xn  xn–1).f(xn)
ÜT 
ba

n
n
 f(xk ) dir.
k 1
Riemann Toplamý
rk  [xk – 1 , xk] için, mk  f(rk)  Mk olacak biçimde
y
f(rk) değeri vardır. xk = xk – xk – 1 aralık uzunluğu yukarı-
y = f(x)
daki eşitsizlikle çarpılırsa, mk.xk  f(rk).xk  Mk.xk olur.
Bu çarpımlar geometrik olarak düşünüldüğünde, taban uzunluğu xk ve sırasıyla yükseklikleri mk, f(rk) ve Mk
olan dikdörtgenlerin alanları biçiminde yorumlanabilir.
Alt Toplam
0 a=x0 r1 x1 r2 x2 ... xk–1 rk xk ... xn–1 rn xn=b
y
x
y = f(x)
y = f(x) eğrisini kesen n tane dikdörtgenin alanları
toplamına Riemann Toplamı denir ve RT ile gösterilir.
RT  (x1  x0).f(r1)  (x2  x1).f(r2)  ...  (xn  xn–1).f(rn)
ÜT 
0 a=x0 x1 x2
x3 ... xk–1 xk
...
xn–1 xn=b
x
ba

n
n
 f(rk ) dir.
k 1
Buna göre, n  N+ için, AT  RT  ÜT dir.
3
Belirli Ýntegral
Konu Özeti
Eğer bölüntü sayısı, yani n değeri giderek arttırılırsa
b
alt ve üst toplamların eğri altındaki alana yaklaştığı görü-
6.
a
lür. Riemann toplamı da alt ve üst toplamlar arasında kalarak eğri altındaki alana eşit olur. Yani n   için,
7.
lim A T  lim R T  lim Ü T dir.
n
n

b
f(x)dx 
 f(x) dx
a
f(x) fonksiyonu sürekli ve tek fonksiyon ise,
a
n
 f(x)dx  0
Tanım: f, [a, b] kapalı aralığında tanımlı olmak üzere,
b
n
a
k=1
dır.
a
8.
If(x)dx  lim  f (rk).xk
n
f(x) fonksiyonu sürekli ve çift fonksiyon ise,
a

a

f(x)dx  2. f(x)dx tir.
a
limitine f nin a dan b ye belirli integrali denir. Eğer bu
0
limit varsa, f fonksiyonu [a, b] kapalı aralığında integrallenebilir denir.
Ýntegral Hesabýnýn Temel Teoremleri
1. Teorem: f : [a, b]  R fonksiyonu, [a, b] aralığında
Özetle Reimann toplamına belirli integral diyebiliriz.
x
sürekli ve F: [a, b]  R fonksiyonu, F(x) 
Teorem: f, [a, b] kapalı aralığında integrallenebilir ise,
b
n
a
k=1
a
b–a
b–a
If(x)dx  nlim
 .f a  k. dir.
n ‰
 n
lim
n
1

n
n
1
 f  n    f(x)dx
k
k 1
elde edilir.
0
şeklinde tanımlanmış olsun. Bu durumda, F(x) fonksiyonu (a, b) aralığında türevlenebilir ve x0  (a, b)
Bireysel Yetenek
Bu teoremde a = 0 ve b = 1 alınırsa,
If(t)dt
için, F '(x0)  f(x0) dır.
Leibniz Kuralý
f(x), [a, b] aralığında sürekli, g(x) ve h(x) bu aralıkta
türevlenebilen iki fonksiyon olsun.
h(x)
Belirli Ýntegralin Özellikleri
F(x) 
f: [a, b]  R , g: [a, b]  R fonksiyonları [a, b] aralı-

f(t)dt olmak üzere,
g(x)
ğında integrallenebilen iki fonksiyon olmak üzere,
F '(x) = f • h(x)œ . h'(x) – f • g(x)œ . g'(x) tir.
a
1.
 f(x)dx  0
2. Teorem: f: [a, b]  R , sürekli bir fonksiyon olsun.
a
b
2.
b
a
a
b
b
3.

b

a
b
5.

a
If(x)dx  F(x)/  F(b) – F(a) dır.
a
a
b

k.f(x)dx  k. f(x)dx , k  R
a
4.
F '(x) = f(x) olmak üzere,
 f(x)dx   f(x)dx
b
Diferansiyel Kavramý
a
c
b

Tanım: y = f(x) fonksiyonu, x noktasında türevli bir

f(x)dx  f(x)dx  f(x)dx , a < c < b
a
dy
fonksiyon olmak üzere,   f '(x) eşitliğinden elde
dx
c
b
b
edilen dy = f '(x).dx ifadesine f(x) in diferansiyeli denir.
a
dy = d •f(x)œ = f '(x).dx tir.
f(x)  g(x) dx  f(x)dx  g(x)dx

a

4
Belirsiz Ýntegral
Konu Özeti
Belirsiz Ýntegral

4.
 e dx  e
5.
 a dx 
6.
 sin xdx   cos x  c
7.
 cos xdx  sin x  c
8.
 sin2 x   (1  cot
9.
 cos2 x   (1  tan
10.
 1 x2
11.

Tanım: Türevi f(x) veya diferansiyeli f(x) dx olan F(x)
fonksiyonuna, f(x) in belirsiz integrali denir ve
If(x)dx = F(x) + c , c  R biçiminde gösterilir.

If(x) dx = F(x) + c eşitliğinde; I işaretine, integral
işareti, f (x) e integrand (integral altındaki fonksiyon),
F(x) fonksiyonuna f (x) in ilkel fonksiyonu ve c ye integral sabiti denir.

F(x) + c yi bulma işlemine, belirsiz integral alma işlemi (integrasyon) denir.

F(x) in x e göre türevi f(x) olmak üzere,
d
F(x)  c   F '(x)  f(x) tir.
dx
f(x) in integralini bulmak, türevi f(x) e eşit olan fonksiyonu bulmaktır.
x
x
eşittir.
2.
'
d 
f(x)dx    f(x)dx   f(x)
 

dx 


Belirsiz integralin diferansiyeli, integral işaretinin al-
Bireysel Yetenek
Belirsiz integralin türevi, integrali alınan fonksiyona
tındaki ifadeye eşittir.
c
ax
c , a > 0 , a  1
ln a
dx
dx
2
x) dx   cot x  c
2
x) dx  tan x  c
 arctan x  c1  arc cot x  c 2
dx
1 x2
 arcsin x  c 1  arc cos x  c 2
Ýntegral Alma Yöntemleri
A. Deðiþken Deðiþtirme Yöntemi
f(x) ve g(x) tanımlı olduğu aralıkta türevlenebilen iki
fonksiyon olsun.

d  f(x)dx   f(x)dx


3.
x
dx
Belirsiz Ýntegralin Özellikleri
1.
dx
 ln x  c
x
3.
1.
Bir fonksiyonun diferansiyelinin belirsiz integrali, bu
 f(x).f '(x)dx
integralinde, f(x) = u dönüşümü yapılır.
f '(x)dx = du olur. Bu durumda,
fonksiyon ile bir c sabitinin toplamına eşittir.

 d f(x)   f '(x)dx  f(x)  c
4.
İntegral içindeki sabit çarpan, integral dışına alınabilir.
k  R olmak üzere,
5.
2.
 k.f(x)dx  k. f(x)dx

f(x).f '(x)dx  u.du 
n
 f(x) .f '(x)dx
u2
f 2(x)
c 
 c dir.
2
2
integralinde, f(x) = u dönüşümü ya-
pılır. f '(x) dx = du olur. Bu durumda,
İki fonksiyonun toplamının veya farkının integrali
n
n
 f(x) .f '(x)dx   u .du 
 f(x)  g(x)  dx   f(x)dx   g(x)dx
n 1
f(x)
un 1
c 
n 1
n 1
c
bulunur.
Ýntegral Alma Kurallarý
3.
1.
 adx  a dx  ax  c
2.

xndx 
, a, c  R

f '(x)
dx integralinde, f(x) = u dönüşümü yapılır.
f(x)
f '(x)dx = du olur. Bu durumda,
xn 1
 c , n  R – {–1}
n 1

5
f '(x)
dx 
f(x)

du
 ln u  c  ln f(x)  c bulunur.
u
Belirsiz Ýntegral
4.
a
f(x)
Konu Özeti
.f '(x)dx a  R+ – {1} integralinde, f(x) = u döˆ
nüşümü yapılır. f '(x)dx = du olur. Bu durumda,
a
5.

f(x)

.f '(x)dx  a udu 
au
a f(x)
c 
 c dir.
ln a
ln a
a, b  R – {0} olmak üzere,




f g(x).g '(x)dx integralinde, g(x) = u dönüşümü
yapılır. g'(x)dx = du olur. Bu durumda,
 f g(x).g '(x)dx   f(u)du
gibi basit fonksiyon in-
6.
İntegrandında sadece
2
a x
2
a x
2
,
2
x a
2
veya
a x
2
dx
2
2 2
a b x

1
 bx 
arcsin 
c
b
 a 
m, n  R , m  0 , a  R+ – {1} olmak üzere,

e
mx n
dx 
1 mx n
c
e
m

a
mx n
dx 
1
a mx n  c
m.ln a
tegrali elde edilir.
2
 x 
 arcsin    c
 a 
dx
2
köklü ifadelerinden birini bulunduran in-
tegraller, trigonometrik dönüşümler yardımıyla hesaplanabilir.
İntegralde
a2  x 2
varsa (a > 0), x = asint dönü-
m, n  R , m  0 olmak üzere,
1

 sin(mx  n)dx   m cos(mx  n)  c

 cos(mx  n)dx 
a2  x 2  a 2  a 2 sin 2 t  a | cos t | olur.
İntegralde
2
x a
2
varsa x = asect dönüşümü ya-
pılır. Bu durumda, dx = asect.tantdt ve
Bireysel Yetenek
şümü yapılır. Bu durumda, dx = acostdt ve
x 2  a 2  a 2 sec 2 t  a 2  a | tan t | olur.
İntegralde
a2  x 2
1
sin(mx  n)  c
m
B. Kýsmi (Parçalý) Ýntegrasyon Yöntemi
Çarpım şeklinde olup, değişken değiştirme yöntemi
uygulanamayan fonksiyonların integralinde kullanılır. u ve
v türevlenebilen iki fonksiyon olmak üzere, çarpım fonksiyonunun diferansiyeli, d(u.v) = du.v + dv.u dur. Buradan,
u.dv = d(u.v) – du.v yazılarak her iki tarafın integrali alınırsa
varsa (a > 0), x = atant dönü-
 u.dv   d(u.v)   v.du  u.dv  u.v   v.du
şümü yapılır. Bu durumda, dx = asec2t.dt ve
elde edilir.
a2  x 2  a 2  a 2 tan 2 t  a | sec t | olur.
Genel olarak logaritmik, ters trigonometrik, polinom,
trigonometrik ve üstel fonksiyonlardan herhangi ikisinin çar7.
m
ax  b ve
n
ax  b köklü ifadelerini bulunduran
pımını bulunduran integrallerde bu sıraya göre, (LAPTÜ)
önce gelen u diğeri dv olarak seçilir.
integral hesabında; ekok(m, n) = k olmak üzere,
ax + b = uk dönüşümü yapılır. Böylece fonksiyon
Sonuç: f(x) polinom fonksiyon olmak üzere,
kökten kurtarılır ve integral işlemine devam edilir.
 f(x).e dx  f(x)  f '(x)  f ''(x)  L.e
x
x
 c dir.
Sonuçlar
a, b  R – {0} olmak üzere,


dx
 a2  x 2
dx
C. Basit Kesirlere Ayýrma Yöntemi
1
 x 

arctan    c
a
 a 
 a 2  b 2x 2
P(x) ve Q(x) ortak çarpanı olmayan iki polinom olmak üzere,
1
 bx 

arctan 
c
ab
 a 
P(x)
 Q(x)
integrali payın ve paydanın derece-
lerine göre farklı iki yöntemle sonuçlandırılır.
6