DERS 12 Belirli İntegral 12.1. Bir eğri altında kalan alan. Bir [a , b

DERS 12
Belirli İntegral
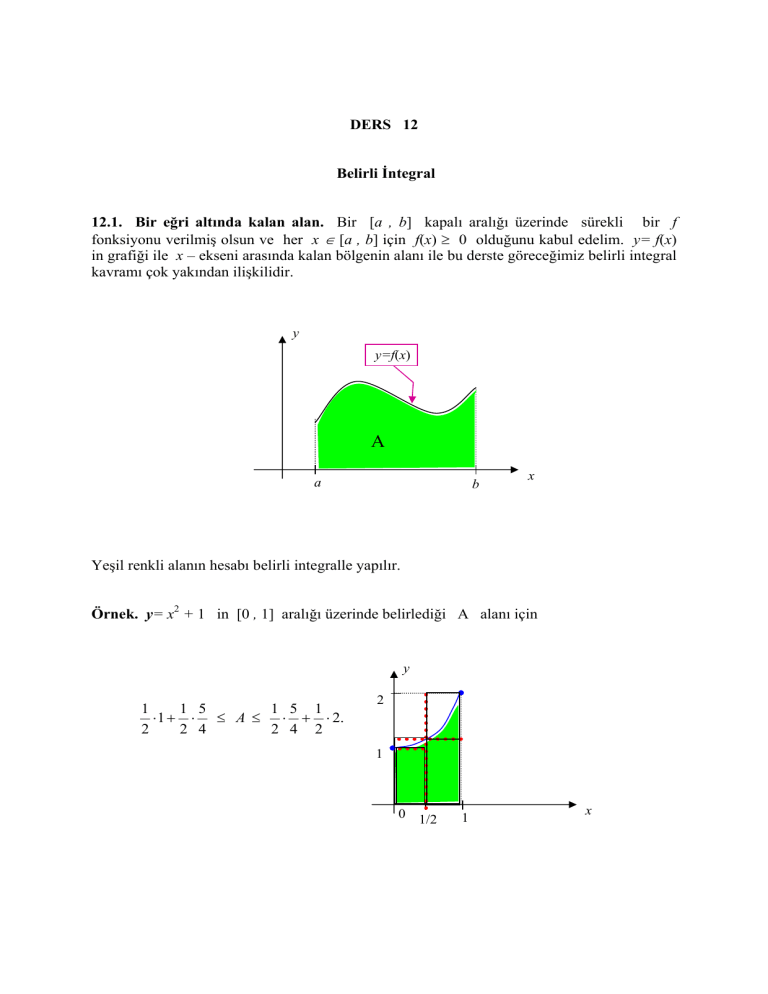
12.1. Bir eğri altında kalan alan. Bir [a , b] kapalı aralığı üzerinde sürekli bir f
fonksiyonu verilmiş olsun ve her x ∈ [a , b] için f(x) ≥ 0 olduğunu kabul edelim. y= f(x)
in grafiği ile x – ekseni arasında kalan bölgenin alanı ile bu derste göreceğimiz belirli integral
kavramı çok yakından ilişkilidir.
y
y=f(x)
A
a
b
x
Yeşil renkli alanın hesabı belirli integralle yapılır.
Örnek. y= x2 + 1 in [0 , 1] aralığı üzerinde belirlediği A alanı için
y
1
1 5
1 5 1
⋅ 1 + ⋅ ≤ A ≤ ⋅ + ⋅ 2.
2
2 4
2 4 2
2
1
0 1/2
1
x
12.2. Belirli integral, Riemann Toplamları. Bir [a , b] kapalı aralığı üzerinde sürekli bir
f fonksiyonu verilmiş olsun.
y
(c1 , f(c1))
a=x0 < x1 < x2 < x3 < . . . < xn-2 < xn-1 < xn=b
ck ∈ (xk-1 , xk)
, 1≤ k ≤ n
∆xk = xk – xk-1 , 1 ≤ k ≤ n
c2
c1
x0= a
x1
cn-2
c3
x3
x2
cn-1
xn-2
xn-3
cn
xn-1
x
b =xn
y = f(x)
n
Tn = f(c1) ∆ x1 + f(c2) ∆ x2 + . . . + f(cn) ∆ xn =
∑ f (c )∆x
k =1
k
k
toplamına bir Riemann Toplamı denir.
Burada ∆ xk lardan her biri sıfıra yaklaşırken (ki bu durumda n sayısı da sonsuza yaklaşır)
Tn Riemann toplamının limit değerine f fonksiyonunun [a , b] kapalı aralığı üzerinde belirli
integrali (definite integral) denir ve bu integral
∫
b
integralin üst sınırı
f ( x ) dx
a
integralin alt sınırı
sembolü ile gösterilir.
n
Tn = f(c1) ∆ x1 + f(c2) ∆ x2 + . . . + f(cn) ∆ xn =
Riemann Toplamı:
Belirli İntegral:
∫
b
a
∑ f (c )∆x
k =1
k
k
f ( x) dx = lim Tn
∆xk → 0
= lim ( f (c1 )∆x1 + f (c2 ) ∆x2 + L + f (cn )∆xn )
∆xk → 0
Belirli İntegralin Bazı Özellikleri.
∫ f ( x) dx
1. Eğer her x∈ [a , b] için f(x) ≥ 0 ise,
belirli integrali , [a , b] aralığı
üzerinde y = f(x) in grafiği ile x – ekseni arasında kalan alanı verir.
2.
∫a (k ⋅ f ( x))dx = k ⋅∫a f ( x) dx
3.
∫a ( f ( x) m g ( x)) dx = ∫a
b
b
b
b
4. a < c < b için
∫
b
a
b
f ( x) dx m ∫ g ( x) dx
a
c
b
a
c
f ( x) dx = ∫ f ( x) dx + ∫ f ( x) dx
12.3. Kalkülüs’ün Temel Teoremi(Fundamental Theorem of Calculus).
belirli integral ile belirsiz integral arasındaki ilişkiyi verir:
Bu teorem
Kalkülüs’ün Temel Teoremi. f fonksiyonu [a , b] kapalı aralığında sürekli ve f nin bir
ters türevi F ise,
∫
b
a
f ( x) dx = F (b) − F (a )
dir.
b
Gösterim. F ( x ) a = F (b) − F ( a )
F ' ( x) = f ( x)
Örnek.
∫ (2 x + 1)dx = x
1
2
⇒
∫
b
a
b
f ( x) dx = F ( x) = F (b) − F (a)
a
+ x = (1 + 1) − (0 + 0 ) = 2.
1
0
0
y
A
C
a
b
B
y = f(x)
∫
b
a
f ( x) dx = A − B + C
x
Örnek.
∫(
1
0
1
)
x3
4
⎛1 ⎞
x + 1 dx = + x = ⎜ + 1⎟ − (0 + 0) = .
3
3
⎝3 ⎠
0
2
y
2
y = x2+1
1
(
A
0
∫
2
∫
5
1
(
2x
dx = ?
x + 10
u= x2 + 10
∫
0
)
, du = 2x dx .
2x
1
dx = ∫ du = ln u = ln (x 2 + 10) + C
x + 10
u
∫
5
x
1
4⎞
⎛
x
2
x
2
2
⎜ 2 x + 3e − ⎟ dx = x + 3e − 4 ln x = 4 + 3e − 4 ln 2 − (1 + 3e − 0 ) = 3(1 + e − e) − 4 ln 2.
x
⎝
⎠
2
0
)
1
4
A = ∫ x 2 + 1 dx = .
0
3
2
5
2x
2
(
)
dx
=
ln
x
+
10
= ln 35 − ln 10 = ln (3.5).
0
x 2 + 10
12.4. Belirli integralde değişken değiştirme.
Son örneğimizde belirli integrali hesaplarken, ters türevin, yani belirsiz integralin belirlen-mesinde değişken değiş-tirme
yöntemini kullandık. Bu yöntemi doğrudan doğruya belirli integral üze-rinde de
uygulayabiliriz. Hatta bu durumda zaman kazanılacağı da söylenebilir.
u = g(x) , du = g´(x) dx
x=a ⇒ u=g(a) ; x=b ⇒ u =g(b)
∫
b
a
F ' ( g ( x )) g ' ( x ) dx =
∫
g (b )
g (a)
F ' (u ) du = F ( u )
g (b )
g (a )
= F ( g ( b )) − F ( g ( a ))
Son örneğimizi bu yolla yapalım:
∫
5
0
2x
dx =
2
x + 10
1
35
∫10 u du = ln u 10 = ln 35 − ln 10 = ln (3.5).
35
u = x2 + 10 , du = 2x dx
x=0 ⇒ u=10 ; x=5 ⇒ u =35
Başka bir örnek:
1
∫
0
x 3 x 2 + 1 dx =
∫
4
1
3
2
4
1
u du = 1 ⋅ u
6
6 3
2
1 32
= ⋅u
9
4
=
1
1
(8 − 1) = 7 .
9
9
1
u = 3x2 + 1 , du = 6x dx , x dx = (1/6) du
x=0 ⇒ u=1 ; x=1 ⇒ u =4
Başka bir örnek:
∫ (e
1
0
2x
)(
)
− 2 x e 2 x − 1 dx =
∫
e 2 −2
1
2
2 e −2
2
e −2
1
2
1 u
1 2
1
1
= ⋅u
= (e2 − 2) − .
u du = ⋅
2 21
4 1
4
4
2
u = e2x – 2x , du = (2e2x – 2) dx , (e2x – 1) dx = (1/2) du
x=0 ⇒ u=1 ; x=1 ⇒ u =e2 - 2
Uygulama. Haftada x televizyon ünitesi üreten bir işletmenin haftalık marjinal kârı, YTL
olarak, P´(x) = 165 - (0.1)x , 0 ≤ x ≤ 4000 biçiminde veriliyor. Şu anda haftada 1500
ünite üreten firma, haftalık üretimini artırmak istiyor. Haftalık üretimini 1600 e çıkarırsa,
haftalık kârındaki değişim ne olacaktır?
Çözüm. Kârdaki artış
1600
P (1600) − P(1500) = P( x) 1500 = ∫
1600
P' ( x) dx
1500
1600
=∫
1500
(165 − (0.1)x ) dx = 165 x − (0.05)x 2 1500
1600
= 165 ⋅1 600 − 0.05 ⋅ 2 560 000 − (165 ⋅1500 − 0.05 ⋅ 2 250 000 )
= 16500 − 0.05 ⋅ 31 000 = 16500 − 15 500 = 1000
YTL olur.
Daha önce belirsiz integral hesabında kullandığımız kısmî integrasyon yöntemini belirli
integral hesaplarken de kullanabiliriz.
Örnek.
∫
1
0
x e x dx = ∫ u dv = uv − ∫ vdu = xe x − ∫ e x dx = xe x − e x = 0 − (− 1) = 1.
1
0
u=x
du = dx
, dv = ex dx
, v = ex
Bazı integrallerin hesabında değişken değiştirme ve kısmî integrasyon yöntemleri birlikte
kullanılabilir.
Örnek.
∫ x ln (x
1
0
2
)
+ 1 dx =
1
⎛1⎞
∫ (ln t ) ⎜⎝ 2 ⎟⎠dt = 2 ∫ (ln t ) dt
2
1
2
1
1⎛
⎛1⎞ ⎞
= ⎜⎜ (t ln t ) − ∫ t ⎜ ⎟dt ⎟⎟
2⎝
⎝t ⎠ ⎠
2
t= x2 + 1
, dt= 2x dx , x dx = (1/2) dt
x=0⇒ t=1 , x=1⇒t=2
u = ln t
, dv = dt
du = (1/t) dt ,
v=t
=
1
((t ln t ) − t ) = 1 (2 ln 2 − 2 − (0 − 1))
2
2
1
1
1
= (2 ln 2 − 1) = ln 2 − .
2
2
12.5. İntegral için ortalama değer teoremi.
sürekli ise, öyle bir c∈ (a , b) vardır ki
b
∫
a
f
fonksiyonu [a , b] kapalı aralığında
f (x) dx = (b − a) f (c)
dir.
y
(c , f(c))
f (c ) =
b
1
f ( x) dx
(b − a) ∫a
a
c
f fonksiyonunun [a , b] aralığı üzerinde ortalama değeri
(Average value of f on the interval [a , b] )
Örnek. f(x) = x - 3x2
nin [-1 , 2] aralığı üzerinde ortalama değeri
2
2
1 x2
1⎛
1
5
1
⎞
2
f (c ) =
(
x
−
3
x
)
dx
=
( − x 3 ) = ⎜ 2 − 8 − ( − (−1)) ⎟ = − .
∫
1
−
(2 − (−1))
3 2
3⎝
2
2
⎠
−1
b
x
12.6. Alan Hesabı. Bir eğri ile x-ekseni arasında kalan alan.
y
y = f(x)
b
A = ∫ f ( x) dx
a
A
a
f(x) ≥ 0
,
x ∈ [a , b]
x
b
y
a
b
x
A
y = f(x)
b
A = − ∫ f ( x) dx
a
f(x) ≤ 0
,
x ∈ [a , b]
y
y =f (x)
a
b
x
d
c
b
c
d
a
b
c
A = ∫ f ( x) dx − ∫ f ( x) dx + ∫ f ( x) dx
Boyalı Alan : A
Örnek. f(x) = 6x – x2
y
1≤ x≤4
,
ile verilen bölgenin alanı.
y = 6x – x2
4
(
4
)
A = ∫ 6 x − x 2 dx = 3x 2 −
1
x3
3 1
43 ⎛ 3 13 ⎞
= 3 ⋅ 4 − − ⎜⎜ 3 ⋅1 − ⎟⎟
3 ⎝
3⎠
63
= 45 −
= 24.
3
2
A
1
3
Örnek. f(x) = x2 - 2x ,
x
4
1 ≤ x ≤2
ile verilen bölgenin alanı.
y
2
(
)
A = − ∫ x 2 − 2 x dx
1
2
1
⎛ x3
⎞
= − ⎜⎜ − x 2 ⎟⎟
⎝ 3
⎠1
2
x
A
y = x2 – 2x
⎛8
⎞ ⎛1 ⎞
= −⎜ − 4 ⎟ + ⎜ − 1⎟
⎝3
⎠ ⎝3 ⎠
7
2
= − +3= .
3
3
Örnek. f(x) = x2 - 2x ,
-1 ≤ x ≤ 1
ile verilen bölgenin alanı.
y
0
(
)
1
(
)
A = ∫ x − 2 x dx − ∫ x 2 − 2 x dx
−1
2
0
0
1
⎞
⎛ x3
⎛ x3
2⎞
= ⎜⎜ − x ⎟⎟ − ⎜⎜ − x 2 ⎟⎟
⎠0
⎠ −1 ⎝ 3
⎝ 3
y = x2 – 2x
⎛ −1 ⎞ ⎛ ⎛ 1 ⎞ ⎞
= 0 − ⎜ − 1⎟ − ⎜⎜ ⎜ − 1⎟ − 0 ⎟⎟
⎝ 3
⎠ ⎝⎝ 3 ⎠ ⎠
1
x
-1
1
1
= + 1 − + 1 = 2.
3
3
12.7. İki Eğri Arasında Kalan Alan. f ve g [a , b ] aralığında sürekli fonksiyonlar, her
x ∈ [a , b ] için g(x) ≤ f(x) olsun . Bu durumda y = f(x) in grafiği y = g(x) in grafiğinin
yukarısındadır ve [a , b ] aralığı üzerinde bu iki eğri arasında kalan alan integral olarak şöyle
ifade edilir:
y = f(x)
y
A
A = ∫ ( f ( x) − g ( x) ) dx
b
a
y = g(x)
a
b
x
Örnek. f(x) = 2x +3 , g(x) = -x2 + 1 , 0≤ x ≤ 2
y
A=∫
ile verilen bölgenin alanı.
((2 x + 3) − (− x
2
0
=∫
y = 2x + 3
2
0
(x
2
2
))
+ 1 dx
)
+ 2 x + 2 dx
2
⎛ x3
⎞
= ⎜⎜ + x 2 + 2 x ⎟⎟
⎝ 3
⎠0
A
32
8
= +4+4 = .
3
3
x
1 2
y = -x2 + 1
İki eğri arasında kalan alan hesaplanırken, y = f(x) in grafiğinin bir kısmı y = g(x) in
grafiğinin yukarısında, bir kısmı da aşağısında olabilir. Bu durumda söz konusu aralık alt
aralıklara bölünerek alan hesaplanır. Örnek olarak aşağıdaki şekilde gösterilen bölgenin
alanına bakalım.
y = f(x)
y
a
c
b
x
A : Boyalı alan
y = g(x)
A = ∫ ( f ( x) − g ( x) ) dx + ∫ ( g ( x) − f ( x) ) dx
c
b
a
c
Örnek. f(x) = -x +1 , g(x) = x2 - 1 , 0≤ x ≤ 2
ile verilen bölgenin alanı.
y
1
A= ∫
0
2
y=x -1
((− x +1) − (x −1)) dx
+ ∫ ((x − 1) − (− x + 1)) dx
2
2
2
1
1
(
)
2
(
)
= ∫ − x2 − x + 2 dx+ ∫ x2 + x − 2 dx
0
1
x
2
y = -x + 1
1
1
2
⎛ x3 x2
⎞ ⎛ x3 x2
⎞
= ⎜⎜ − − + 2x ⎟⎟ + ⎜⎜ + − 2x ⎟⎟
⎝ 3 2
⎠0 ⎝ 3 2
⎠1
⎛ 1 1
⎞ ⎛8
⎛1 1
⎞⎞
= ⎜ − − + 2 − 0 ⎟ + ⎜⎜ + 2 − 4 − ⎜ + − 2 ⎟ ⎟⎟
⎝ 3 2
⎠ ⎝3
⎝3 2
⎠⎠
= 3.
12.8. Hacim Hesabı , Dönel Cisimlerin Hacmi. Düzlemde bir bölgenin x-ekseni etrafında
döndürülmesiyle meydana gelen cismin hacmi integral yardımıyla hesaplanabilir.
y
y = f(x)
Cismin Hacmi : V
f(x)
a
dx
V = π ∫ ( f (x)) dx
b
b
Silindirin Hacmi : dV
x
a
dV = π ( f ( x) ) dx
2
2
Örnek. f(x) = x2
, 0≤ x≤1
ile verilen bölgeyi x - ekseni etrafında döndürünce
meydana gelen cismin hacmini hesaplayalım.
y
( )
1
y=x
2
V = π ∫ x2
2
0
dx
1
=π ∫ x4 dx
0
1
π
x5
=π
= .
5 0 5
x
1
Örnek(Kürenin hacmi). Yarıçapı r birim olan küre, yarıçapı r birim olan bir yarım
çemberin çapı etrafında döndürülmesiyle elde edilir. Dolayısıyla, sözü edilen hacim
f(x)= (r2 - x2 )1/2 , -1 ≤ x ≤ 1 eğrisinin x - ekseni etrafında döndü-rülmesiyle elde edilir.
y
V =π∫
r
−r
y = r 2 − x2
=π
(r
∫ (r
r
−r
2
2
− x2
) dx
2
)
− x 2 dx
r
-r
r
x
⎛ 2
x3 ⎞
= π ⎜⎜ r x − ⎟⎟
3 ⎠ −r
⎝
⎛
r3 ⎛
r 3 ⎞ ⎞ 4πr 3
.
= π ⎜⎜ r 3 − − ⎜⎜ − r 3 + ⎟⎟ ⎟⎟ =
3
3
3
⎠
⎝
⎝
⎠
Örnek(Koninin hacmi). Taban yarıçapı
r birim ve yüksekliği h birim olan koni,
f(x) = (r/h)x , 0 ≤ x ≤ h
eğrisinin x - ekseni etrafında döndürülmesiyle elde edilir.
y
V =π∫
h
0
y = (r / h) x
=π
((r / h) x )2
∫
h
0
dx
⎛ r2 2 ⎞
⎜⎜ 2 x ⎟⎟ dx
⎝h
⎠
h
h
x
⎛ r 2 x3 ⎞
⎟⎟
= π ⎜⎜ 2
⎝h 3 ⎠0
⎛ r 2 h3 ⎞ π 2
= π ⎜⎜ 2 ⋅ ⎟⎟ = r h.
⎝h 3 ⎠ 3
Problemler 12
1. Aşağıdaki belirli integralleri hesaplayınız.
2
a) ∫ (2 x − 2 − 3)dx
1
10
d)
∫e
− 0.05 x
4
b) ∫ 3 x dx
1
3
e)
−5
∫
7
4 − 2 x dx
ç)
2
0
dx
5
c) ∫ 12( x 2 − 4) 5 xdx
f)
−6
∫
−1
x
x+2
1
∫ x − 1 dx
3
1
g) ∫ (e 2 x − 2 x)(e 2 x − 1)dx
dx
0
2. Aşağıdaki belirli integralleri hesaplayınız.
1
a)
x
∫ ( x + 1)e dx
0
3
ç)
4
∫ 10(2 x − 1) dx
0
e
3
b) ∫ ln(2 x) dx
c)
1
1
10
d)
∫ 10e
0
−0.02 x
∫
ln x
x
2
dx
e)
∫
2
dx
e−x
−x
1 1 + 2e
dx
3. Dağ bisikleti üreten bir firmanın araştırma departmanı, marjinal gider fonksiyonunu,
ayda
x adet bisiklet üretilmesi durumunda, C´(x) = 500 −
3
, 0 ≤ x ≤ 900 olarak
x
belirliyor. 300 bisikletlik bir üretim seviyesinden 900 bisikletlik bir üretim seviyesine
geçilmesi durumunda toplam giderde ne kadar artış olacağını bir belirli integral olarak
ifade edip hesaplayınız.
4. Aşağıdaki şekilde verilen alanları belirli integraller olarak ifade ediniz:
y
y = f(x)
0
a
c
b
d
x
a) [a , b] aralığı ile grafik arasındaki alan. b) [b , c] aralığı ile grafik arasındaki alan.
c) [c , d] aralığı ile grafik arasındaki alan.
ç) [a , c] aralığı ile grafik arasındaki alan.
d) [b , d] aralığı ile grafik arasındaki alan.
e) [a , d] aralığı ile grafik arasındaki alan.
5. Aşağıda verilen eğriler ile verilen aralık üzerinde çevrelenmiş bölgelerin alanlarını
bulunuz.
a) y = 3 x 2 , y = 0 ; 1 ≤ x ≤ 2
b) y = −2 x − 1 , y = 0 ; 0 ≤ x ≤ 4
c) y = x 2 + 2 , y = 0 ; − 1 ≤ x ≤ 0
ç) y = e x , y = 0 ; − 1 ≤ x ≤ 2
d) y =
−1
, y = 0 ; 0.5 ≤ t ≤ 1
t
e) y = −2 x + 8 , y = 12 ; − 1 ≤ x ≤ 2
f) y = x 2 + 1 , y = 2 x − 2 ; − 1 ≤ x ≤ 2 g) y = x3 , y = x ; − 2 ≤ x ≤ 2
6. Aşağıda verilen iki eğri arasında kalan bölgenin alanını bulunuz.
a) y = 3 x 2 , y = 12
b) y = 4 − x 2 , y = −5
c) y = x3 , y = 4 x
ç) y =
d) y = 2 − x , y = x 2
e) y = x 4 − 6 x 2 , y = 4 x 2 − 9
x,y=x
7. Alıştırma 6 da verilen bölgelerin x – ekseni etrafında döndürülmesiyle elde edilen
cisimlerin hacimlerini bulunuz.