Heat Capacity and Specific Heat
• Fonon (Phonon) – Elastik dalga paketidir. Enerjisi,
dalga boyu veya frekansı ile karakterize edilir ki bu
enerji malzemeye transfer edilir.
• Özgül ısı (Specific heat) – bir gram malzemenin
sıcaklığını bir derece arttırmak için gereken enerji
miktarıdır.
Figure 21.1 Heat capacity as a function of temperature for
metals and ceramics.
Figure 21.2 The effect of temperature on the specific heat of
iron. Both the change in crystal structure and the change from
ferromagnetic to paramagnetic behavior are indicated.
Specific Heat of Tungsten
How much heat must be supplied to 250 g of tungsten to raise
its temperature from 25oC to 650oC?
Example 21.1 SOLUTION
If no losses occur, 5000 cal (or 20,920 J) must be supplied to
the tungsten.
Thermal Expansion
Lineer termal uzama katsayısı (Linear coefficient of thermal
expansion) – Sıcaklığı bir derece arttırıldığında malzemenin
birim boyutunda meydana gelen değişimi ifade eder.
Isıl gerilmeler (Thermal stresses) – Sıcaklıklarda meydana
gelen değişimin, malzeme hacminin farklı noktalarında
meydana gelen genleşme veya büzülme farklarından dolayı
meydana gelen gerilmelerdir
The relationship between the linear coefficient of thermal
expansion and the melting temperature in metals at 25°C. Higher
melting point metals tend to expand to a lesser degree.
(a) The linear coefficient of thermal expansion of iron
changes abruptly at temperatures where an allotropic
transformation occurs. (b) The expansion of Invar is very
low due to the magnetic properties of the material at low
temperatures.
Example:Bonding and Thermal Expansion
Explain why, in Figure, the linear coefficients of thermal
expansion for silicon and tin do not fall on the curve. How
would you expect germanium to fit into this figure?
Figure 21.3 The
relationship between
the linear coefficient
of thermal expansion
and the melting
temperature in
metals at 25°C.
Higher melting point
metals tend to
expand to a lesser
degree.
Example SOLUTION
Both silicon and tin are covalently bonded. The strong
covalent bonds are more difficult to stretch than the
metallic bonds (a deeper trough in the energy-separation
curve), so these elements have a lower coefficient. Since
germanium also is covalently bonded, its thermal
expansion should be less than that predicted by Figure
21.3.
Example: Design of a Pattern for a Casting
Process
Design the dimensions for a pattern that will be used to
produce a rectangular-shaped aluminum casting having
dimensions at 25oC of 25 cm 25 cm 3 cm.
Example 21.4 SOLUTION
The linear coefficient of thermal expansion for aluminum is 25
10-6 1/oC. The temperature change from the freezing
temperature to 25oC is 660 - 25 = 635oC. The change in any
dimension is given by:
For the 25-cm dimensions, lf = 25 cm. We wish to find l0 :
Example: SOLUTION (Continued)
For the 3-cm dimensions, lf = 3 cm.
If we design the pattern to the dimensions 25.40 cm
25.40 cm 3.05 cm, the casting should contract to the
required dimensions.
Example:Design of a Protective Coating
A ceramic enamel is to be applied to a 1020 steel plate. The
ceramic has a fracture strength of 4000 psi, a modulus of
elasticity of 15 106 psi, and a coefficient of thermal expansion
of 10 10-6 1/oC. Design the maximum temperature change
that can be allowed without cracking the ceramic.
Example: SOLUTION
If only the enamel heated (and the steel remained at a
constant temperature), the maximum temperature change
would be:
However, the steel also expands. Its coefficient of thermal
expansion (Table 21-2) is 12 10-6 1/oC and its modulus
of elasticity is 30 106 psi. The net coefficient of
expansion is
Thermal Conductivity
Termal iletkenlik (Thermal conductivity) – mikroyapıya
bağımlı ve malzeme içerisinde ısı transfer hızının ölçüsü
olan bir malzeme özelliğidir.
Lorentz sabiti – elektrik ve termal özellikleri ilişkilendiren
bir katsayıdır.
©2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.
Figure: When one end of a bar is heated, a heat flux Q/A
flows toward the cold ends at a rate determined by the
temperature gradient produced in the bar.
Figure: The effect of
temperature on the
thermal conductivity
of selected
materials. Note the
log scale on the yaxis.
©2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.
Example:Design of a Window Glass
Design a glass window 4 ft 4 ft square that separates a
room at 25oC from the outside at 40oC and allows no more
than 5 106 cal of heat to enter the room each day. Assume
thermal conductivity of glass is 0.96 W . m-1 K-1 or 0.023
cal/cm . s . K.
Example 21.6 SOLUTION
where Q/A is the heat transferred per second through the
window.
Example: SOLUTION (Continued)
Thermal Shock
Termal şok (Thermal shock) – Sıcaklıktaki ani değişimler
sonucu oluşan oluşan termal gerilmelerin malzemelerde
oluşturduğu hasardır.
©2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.
Figure: The effect of quenching temperature difference on
the modulus of rupture of sialon. The thermal shock
resistance of the ceramic is good up to about 950°C.
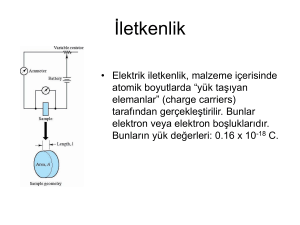
İletkenlik
• Elektrik iletkenlik, malzeme içerisinde
atomik boyutlarda “yük taşıyan
elemanlar” (charge carriers)
tarafından gerçekleştirilir. Bunlar
elektron veya elektron boşluklarıdır.
Bunların yük değerleri: 0.16 x 10-18 C.
V I .R
V: volt, I: akım, R: direnç
R. A
l
1
: öz dirençlik, , A: alan, l: boy
: iletkenlik
n.q.
E
q: yük :C, : hareketlilik (mobility)(m2 /(V.Sn)
N: yük yoğunluğu: 1 /m3
: ortalama hız, m/s, E: elektrik alan, V/m
nn qn n n p q p p
Enerji seviyeleri
Pauli exclusion kuralı: 2 tane elektron yörünge içerisinde aynı yerde
bulunamaz.Her bir yörünge birbirinin tersi spine sahip iki elektrona sahiptir.
Bir Na atomu 3s yörüngede bir elektrona sahiptir. 4 adet Na atomunda 4
elektron Pauli prensibine göre aynı yörüngede bulunamaz. Bu nedenle 3s
yörüngeleri arasında hafif seviye farkı vardır. Aynı zamanda delokolize olan
bu 4 elektron çok hareketlidir ve 4 farklı Na atomları tarafından paylaşılır.
Bu elektronlar aynı zamanda Na atomlarını bir arada tutacak bir bağ
oluştururlar.
Bu komşu yarı dolu 3s yörüngeleri arasındaki mesafe çok
küçüktür ve bir enerji bandı (valans bandı) oluştururlar. Bu
bant içerisindeki yüksek hareketliliğe sahip bu elektronlar
valans elektronları olarak adlandırılırlar ve elektron bulutu
oluşturarak katı malzeme içerisinde sürekli hareket
edebilirler. Sonuç olarak bu yapıya sahip olan metallerin
elektrik iletkenlikleri yüksektir.
Fermi enerji seviyeleri
0 oK sıcaklıkta valans bandının sahip olabileceği en yüksek enerji Fermi
seviyesi olarak adlandırılır. Herhangi bir sıcaklıkta enerji bandının sahip
olabileceği enerji ise 0 ile 1 arasında değer alabilen Fermi fonksiyonu ile
dikkate alınır.
0oK de Ef in üzerinde enerjiye sahip elektron bulunmadığı için malzeme iletken
değildir.Bu nedenle belli bir seviyede, ısı gibi, dış enerjiye ihtiyaç vardır.
f (E)
1
e
( E E f ) / kT
1
K: boltzman sabiti:13.8 x 10-24J/oK)
E>>Ef f(E) = 0
E<<Ef f(E) = 1
E=Ef f(E) = 0.5
T arttıkça f(E) 0 a yaklaşır.
Sonuç olarak metallerde sıcaklık
elektronların fermi seviyesinin
üzerindeki enerji seviyelerinde
bulunmasını sağlayabildiği için iyi
iletkendirler. Bu elektronlara serbest
elektronlar denir.
Elmas gibi kovalent bağa sahip malzemelerde elektronların valans
bandından iletkenlik bandına geçmesi için yenmeleri gereken bir
enerji aralığı (Eg) söz konusudur.
~6eV
~1.107eV
Silisyumda Eg seviyesi Elmasa göre çok
daha düşüktür. Oda sıcaklığı az fakat
önemli sayıda elektronların, arkalarında
boşluk bırakarak (elektron boşlukları (+
yüklü) valans bandından iletkenlik bandına
geçmesine sebep olur. Bu nedenle Si oda
sıcaklığında dahi iletkenlik gösterebilir.
Hem pozitif hem de negatif taşıyıcılar
iletkenlikte etkin olur
İletkenlik
• İletken, yüksek seviyelerde elektrik iletkenliğe sahip
malzemelere verilen isimdir. İletkenlik seviyeleri 10x106 -1m-1
seviyelerindedir.
İletkenlik bu eşitlikle hesaplanır. Yük elektronlar
ne qe e 1 /
ile taşınır.
Artan sıcaklıkla malzemelerde
görülen iletkenlikte düşme
gerçekleşmektedir. Bunun sebebi,
dalga hareketi şeklinde hareket eden
elektronların hareketliliğinin artan
sıcaklıkla titreşimleri artan atomlar
arasındaki etkileşimdir.
rt 1 (T Trt )
: Sıcaklık direnç sabiti
o 1 x
o: saf metalin direnci
: alaşımın direnci
: Sabit
Isıl eleman
• Isıl eleman iki metal telden
oluşur.
• Bu metal tellerin farklı
sıcaklıklara konması durumunda
sıcak taraftaki yüksek enerjiden
dolayı sıcaktan soğuk tarafa
doğru bir elektron akışı
gerçekleşir. Soğuk taraf (-),
sıcak taraf (+) olarak
davranır.Bu etki Seebeck etkisi,
okunan voltajda seebeck voltajı
olarak adlandırılır.
İletkenliğe etki eden faktörler;
• Malzeme türü
• İletkenlik formülünden
– Yük taşıyıcı yoğunluğu
– Hareketlilik
– Yük
ne qe e 1 /
• Sıcaklık
• Kimyasal kompozisyon- alaşım olma durumu
Superiletkenlik
• Metallerin çoğu 0oK sıcaklığa
yaklaştıkça dirençleri sıfır
değildir ve belli oranlarda
iletkenlik gösterirler,
• Bazı malzemeler ise farklı olarak
belli bir Tc kritik sıcaklığının
altında sıfır direnç göstermeye
başlarlar. Bu duruma süper
iletkenlik adı verilir.
• süper iletkenlik, Tc sıcaklığın
altında kafes titreşimi ile dalga
hareketi ile ilerleyen elektronların
uyumu ile gerçekleşmektedir.
1,2,3 Süper iletken YBa2Cu3O7-x
Yalıtkanlık
• Yalıtkanlar, iletkenlik seviyeleri çok düşük olan
malzemelerdir. İletkenlikleri 10-10 – 10-16 -1m-1
seviyelerindedir.
• Enerji aralığı 2 eV un üzerindedir. Yük taşıyıcı olarak
elektron yoğunluğu (ne) çok düşüktür. Bu nedenle
genelde çok küçük seviyelerde olan iletim sıcaklık
nedeniyle değil, iyonik katışkılar sebebiyle olur.
• Endüstride seramiklerin %80ni elektronik
endüstrisinde kullanılır. %20 si yapısal
uygulamalarda kullanılır.
Yalıtkanlar
Kapasitörler yüksek
yalıtkanlık seviyelerine sahip
dielektrik malzemeler
kullanılarak üretilir.
Yüksek E, Elektrik alan
etkisinde dipoller elektrotlar
üzerinde birikir.
D .E o . .E
D: Yük yoğunluğu: C/m2
: elektrik geçirgenlik: C / (V.m)
o: vakumun elektrik geçirgenliği:8.854x10-12 C / (V.m)
Manyetik Özellikler
Manyetizm: Bazı malzemelerin çekime maruz kalmasını ifade eder.
Elektrik akımının kapalı bir çevrimde
akması
manyetik alan oluşumuna neden
olur.
B o .H
B .H
B .H o .( H M )
r
o
B = indüksiyon (akı yoğunluğu), weber /m2
H = Manyetik alan gerilimi, amper/m
= geçirgenlik, weber /amper-m
o = vakumun geçirgenliği
r = kısmi geçirgenlik
Paramanyetik katılar
Diyamanyetik katılar
Ferromanyetik malzemeler, manyetik histerisiz
H=0
S: Doyma
R: Kalıcı
C: Zorlayıcı
Başlangıç geçirgenliği, i
B=0
Manyetik alan aralığı
Eşleşmemiş elektronlar:
Bohr manyetikleşme
etkisine sebep olurlar
Eşleşmiş elektronlar
Eğer komşu atomlarda
elektronlar aynı manyetik
momente sahip olurlarsa ,
bütün hacimde net bir
manyetik etki söz konusu olur.
Bu yapılarda Bs mevcuttur.
Domain
Power generation
Mıknatıs