MAK 212 - TERMODİNAMİK
18.04.2011
2009-2010 BAHAR YARIYILI
ARA SINAV-2
Soru 1-) Hacmi 8 L olan sabit hacimli rijit bir depoda başlangıçta 1200 C sıcaklık ve 0.1 kuruluk
derecesinde su bulunmaktadır. Depo bir vana ile içinden 400 kPa basınçta ve 2000 C sıcaklıkta su akan
bir boruya bağlıdır. Vana açılmakta ve depo içindeki basınç 300 kPa olana kadar açık tutulmaktadır. Bu
sırada depoya 0.4 kg su girmekte ve 250 C sıcaklıktaki çevreye ısı geçişi olmaktadır.
(a) Son halde depo içindeki su kütlesini bulunuz.
(b) Son halde depo içindeki suyun özgül iç enerjisini hesaplayınız,
(c) Hal değişimi sırasında çevreye olan ısı geçişini belirleyiniz.
Soru 2-) Yeni geliştirilen bir ısı makinasının 180 C sıcaklığındaki bir ısı kaynağından çektiği ısı ile
debisi 0,2 kg/s olan 800 kPa basınçtaki doymuş sıvı R-134a soğutucu akışkanını doymuş buhar haline
getirdiği ve bu makinanın 10 kW iş ürettiği ifade edilmektedir.
(a) Bu makinanın verilen şartlarda gerçekleştirilmesinin mümkün olup olamayacağını
hesaplayarak gösteriniz .
(b) Isı makinasının sıcak ısı kaynağından çektiği ısıyı, soğuk ısı kaynağına terkettiği ısı miktarını
ve verimini bulunuz.
(c) Sıcak ve soğuk ısı kaynaklarının ve R-134a soğutucu akışkanın anlık entropi değişimini
hesaplayınız.
Soru 3-) Yatay bir silindir serbest hareket edebilen, sızdırmaz,
sürtünmesiz ve mükemmel bir şekilde yalıtılmış olan bir pistonla iki
bölmeye ayrılmıştır. Başlangıçta pistonun sol tarafında (A) 40°C
sıcaklıkta 0.15 m3 hava, sağ tarafında (B) ise 120°C sıcaklıkta kuruluk
derecesi 0.2 olan 0.15 m3 ıslak su buharı bulunmaktadır. Silindirin her
tarafı, su buharı bulunan taban hariç, yalıtılmıştır. Daha sonra 450 K sıcaklığındaki bir ısı kaynağından
hacmi 0.2 m3 olana kadar suya yavaş yavaş ısı geçişi olmaktadır. Mükemmel gaz olan havanın hal
değişimini izentropik ( k = 1.4 ) ve özgül ısılarını değişken kabul ederek,
(a) Havanın; ilk halde basıncını, son halde basınç ve sıcaklığını, kütlesini,
(b) Suyun kütlesini, son halde sıcaklığını,
(c) Suya olan ısı geçişini,
(d) Bu hal değişiminde; havanın, suyun, ısı kaynağının entropi değişimlerini ve entropi üretimini
hesaplayınız.
HAVA
& = 11.88 m3/dak
V
3
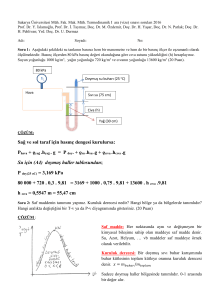
Soru 4-) Hava pencere tipi bir klima cihazının buharlaştırıcısına
100 kPa basınç ve 27oC sıcaklıkta 11.88 m3/dakika debiyle
girmektedir. Soğutucu akışkan-134a ise buharlaştırıcıya 140 kPa
basınçta, 0.3 kuruluk derecesiyle girmekte aynı basınçta doymuş
buhar olarak çıkmaktadır. Soğutucu akışkan-134a’nın debisi 1.81
kg/dakikadır. Her iki akış da süreklidir. 30ºC sıcaklıktaki çevre
ortamdan klima cihazına 33 kJ/dakika ısı geçişi olduğunu kabul
ederek
(a) Havanın çıkış sıcaklığını,
(b) birim zamandaki entropi üretimini hesaplayınız.
(Havayı mükemmel gaz ve özgül ısılarını sabit kabul ediniz.
Özgül ısıların oda sıcaklığındaki değerlerini alınız.)
SA-134a
P1=140 kPa
x1= 0.3
P3=100 kPa
T3=27°C
Tçevre=30ºC
3
1
4
2
P2=140 kPa
x2= 1.0
P4=100 kPa
T4=?
Süre : 120 dakika / Ders notları ve kitaplar kapalıdır. Sınavda kullanılacak Tablolar size verilecektir.
B
A
Ş
A
R
I
L
A
R
Soru 1-) (T) Hacmi 8 L olan sabit hacimli rijit bir depoda başlangıçta 1200 C sıcaklık ve 0.1 kuruluk
derecesinde su bulunmaktadır. Depo bir vana ile içinden 400 kPa basınçta ve 2000 C sıcaklıkta su akan
bir boruya bağlıdır. Vana açılmakta ve depo içindeki basınç 300 kPa olana kadar açık tutulmaktadır. Bu
sırada depoya 0.4 kg su girmekte ve 250 C sıcaklıktaki çevreye ısı geçişi olmaktadır.
(a) Son halde depo içindeki su kütlesini bulunuz.
(b) Son halde depo içindeki suyun özgül iç enerjisini hesaplayınız,
(c) Hal değişimi sırasında çevreye olan ısı geçişini belirleyiniz.
SU
T1 = 120ºC
x1 = 0.1
m1 = ?
Çözüm:
Sistem: Depo (açık sistem, KH, DADA)
Pi = 400 kPa
Ti = 200ºC
P1 = 198.53 kPa
Başlangıç hali : T1 = 120 o C
u 1 = u f + x 1 u fg = 503.5 + 0.1 × 2025.8 = 706.08 kJ / kg
x 1 = 0.1
v1 = v f + x 1 v fg = 0.00106 + (0.1) × (0.8919 − 0.00106 ) = 0.09014 m 3 /kg
m1 =
V1
0.008
=
= 0.089 kg
v1 0.09014
Son hal : P2 = 300 kPa
Giriş hali : Pi = 400 kPa
h = 2860.5 kJ / kg
Ti = 200 o C i
Birinci Yasa: ( W ~ 0, ∆KE ~ 0, ∆PE ~ 0 )
Q d − Wd
(a)
Ê0
+ m i h i = m 2 u 2 − m1 u 1
Kütlenin korunumu:
m 2 = m1 + m i
(b) v 2 =
x2 =
→
m 2 = 0.089 + 0.4 = 0.489 kg
V2 0.008
=
= 0.01637 m 3 / kg , P2 = 300 kPa
m 2 0.489
v 2 − v f 0.01637 − 0.001073
=
= 0.0253
vg − vf
0.6058 − 0.001073
u 2 = u f + x 2 u fg = 561.15 + 0.0253 × 1982.4 = 611.31 kJ / kg
(c) Birinci yasadan:
Q = 0.489 × 611.31 − 0.089 × 706.08 − 0.4 × 2860.5
= 298.8 − 62.66 − 1144.2
= −908.1 kJ
Soru 2-) (N) Yeni geliştirilen bir ısı makinasının 180 C sıcaklığındaki bir ısı kaynağından çektiği ısı ile
debisi 0,2 kg/s olan 800 kPa basınçtaki doymuş sıvı R-134a soğutucu akışkanını doymuş buhar haline
getirdiği ve bu makinanın 10 kW iş ürettiği ifade edilmektedir.
(a) Bu makinanın verilen şartlarda gerçekleştirilmesinin mümkün olup olamayacağını
hesaplayarak gösteriniz .
(b) Isı makinasının sıcak ısı kaynağından çektiği ısıyı, soğuk ısı kaynağına terkettiği ısı miktarını
ve verimini bulunuz.
(c) Sıcak ve soğuk ısı kaynaklarının ve R-134a soğutucu akışkanın anlık entropi değişimini
hesaplayınız.
ÇÖZÜM:
Tdoy= 31.31 C @P=800 kPa hsb= 171.82 kJ/kg
=0.112862
Soru 3-) (L) Yatay bir silindir serbest hareket edebilen, sızdırmaz,
sürtünmesiz ve mükemmel bir şekilde yalıtılmış olan bir pistonla iki
bölmeye ayrılmıştır. Başlangıçta pistonun sol tarafında (A) 40°C
sıcaklıkta 0.15 m3 hava, sağ tarafında (B) ise 120°C sıcaklıkta kuruluk
derecesi 0.2 olan 0.15 m3 ıslak su buharı bulunmaktadır. Silindirin her
tarafı, su buharı bulunan taban hariç, yalıtılmıştır. Daha sonra 450 K sıcaklığındaki bir ısı kaynağından
hacmi 0.2 m3 olana kadar suya yavaş yavaş ısı geçişi olmaktadır. Mükemmel gaz olan havanın hal
değişimini izentropik ( k = 1.4 ) ve özgül ısılarını değişken kabul ederek,
(a) Havanın; ilk halde basıncını, son halde basınç ve sıcaklığını, kütlesini,
(b) Suyun kütlesini, son halde sıcaklığını, (c) Suya olan ısı geçişini,
(d) Bu hal değişiminde; havanın, suyun, ısı kaynağının entropi değişimlerini ve entropi üretimini
hesaplayınız.
Çözüm: (Değişken Özgül Isılar Yaklaşımıyla)
A Tarafı a)
V2 B = 0.2
→
V2 A = 0.3 − V2 B = 0.3 − 0.2 = 0.1
P1 = Pdoyma @120C = 198.67 kPa
Pistonun iki tarafında basınç aynıdır.
PV
198.67 × 0.15 = m × 0.287 × (273 + 40)
m = 0.332kg
1 1 = mRT1
V
0.15
V
0.1
v1 = 1 =
= 0.4518 m3/kg
v2 = 2 =
= 0.3012 m3/kg
m 0.332
m 0.332
Hava tablosundan interpolasyonla;
T1 = 313K
→
vr1 = 558.8
Pr1 = 1.6082
u1 = 223.41kJ / kg
v2 vr 2
v
0.3012
vr 2 = 372.53
= r2
=
0.4518 558.8
v1 vr1
Hava tablosundan interpolasyonla;
vr 2 = 372.53 →
T2 = 367.97 K
Pr 2 = 2.8379
u2 = 262.99kJ / kg
P2
P2 Pr 2
2.8379
P2 = 350.58kPa
=
=
198.67 1.6082
P1 Pr1
B Tarafı b)
v1 = v f + x1v fg = 0.001060 + 0.2(0.89133 − 0.001060) = 0.179114 m3 kg
u1 = u f + x1u fg = 503.60 + 0.2(2025.3) = 908.66 kJ/kg
s1 = s f + x1s fg = 1.5279 + 0.2(5.6013) = 2.64816 kJ/kg.K
V1
0.15
=
= 0.8375kg
v1 0.179114
V
0.2
v2 = 2 =
= 0.2388 m3 kg
m 0.8375
P2 = 350.58 ≈ 350kPa →
v f = 0.001079 m3 kg
m=
v f < v2 < vg olduğundan son hal ıslak buhardır.
x2 =
v2 − v f
v fg
=
vg = 0.52422 m3 kg
T2 = Tdoyma @350 kPa = 138.86C
0.2388 − 0.001079
= 0.4544
0.52422 − 0.001079
s2 = s f + x2 s fg = 1.7274 + 0.4544(5.2128) = 4.0961 kJ/kg.K
u2 = u f + x2u fg = 583.89 + 0.4544(1964.5) = 1476.56 kJ/kg
c) Kapalı Sistem: A ve B’deki toplam kütle
W =0
1. yasa
Q − W = ∆U
Q = ∆U = ∆U A + ∆U B = m ( u2 − u1 ) A + m ( u2 − u1 ) B
Q = [ 0.332(262.99 − 223.41] A + [ 0.8375(1476.56 − 908.66) ]B = 488.76kJ
d) ∆S A = 0
(İzentropik h.d.)
∆S B = m ( s2 − s1 ) B = 0.8375(4.0961 − 2.64816) = 1.2126 kJ/kg.K
Q
−Q
−488.46
∆Skaynak = kaynak =
=
= −1.0855 kJ/kg.K
Tkaynak Tkaynak
450
Süretim = ∆S A + ∆S B + ∆Skaynak = 0 + 1.2126 − 1.0855 = 0.1271 kJ/kg.K
Çözüm: (Sabit Özgül Isılar Yaklaşımıyla)
A Tarafı a)
→
V2 B = 0.2
V2 A = 0.3 − V2 B = 0.3 − 0.2 = 0.1
P1 = Pdoyma @120C = 198.67 kPa
Pistonun iki tarafında basınç aynıdır.
P2 V1
=
P1 V2
T2 V1
=
T1 V2
k
1.4
P2
0.15
=
198.67 0.1
k −1
P2 = 350.48kPa
1.4 −1
T2
0.15
=
273 + 40 0.1
T2 = 368.11K
PV
198.67 × 0.15 = m × 0.287 × (273 + 40)
m = 0.332kg
1 1 = mRT1
Hava tablosundan interpolasyonla;
T1 = 313K
→
u1 = 223.41kJ / kg
T2 = 368.11K →
u2 = 262.99kJ / kg
B Tarafı b)
v1 = v f + x1v fg = 0.001060 + 0.2(0.89133 − 0.001060) = 0.179114 m3 kg
u1 = u f + x1u fg = 503.60 + 0.2(2025.3) = 908.66 kJ/kg
s1 = s f + x1s fg = 1.5279 + 0.2(5.6013) = 2.64816 kJ/kg.K
V1
0.15
=
= 0.8375kg
v1 0.179114
V
0.2
v2 = 2 =
= 0.2388 m3 kg
m 0.8375
P2 = 350.48 ≈ 350kPa →
v f = 0.001079 m3 kg
m=
v f < v2 < vg olduğundan son hal ıslak buhardır.
x2 =
v2 − v f
v fg
=
vg = 0.52422 m3 kg
T2 = Tdoyma @350 kPa = 138.86C
0.2388 − 0.001079
= 0.4544
0.52422 − 0.001079
s2 = s f + x2 s fg = 1.7274 + 0.4544(5.2128) = 4.0961 kJ/kg.K
u2 = u f + x2u fg = 583.89 + 0.4544(1964.5) = 1476.56 kJ/kg
c) Kapalı Sistem: A ve B’deki toplam kütle
Q − W = ∆U
W =0
1. yasa
Q = ∆U = ∆U A + ∆U B = m ( u2 − u1 ) A + m ( u2 − u1 ) B
Q = [ 0.332(262.99 − 223.41] A + [ 0.8375(1476.56 − 908.66) ]B = 488.76kJ
d) ∆S A = 0
(İzentropik h.d.)
∆S B = m ( s2 − s1 ) B = 0.8375(4.0961 − 2.64816) = 1.2126 kJ/kg.K
Q
−Q
−488.46
∆Skaynak = kaynak =
=
= −1.0855 kJ/kg.K
450
Tkaynak Tkaynak
Süretim = ∆S A + ∆S B + ∆Skaynak = 0 + 1.2126 − 1.0855 = 0.1271 kJ/kg.K
Soru 4-) Hava pencere tipi bir klima cihazının buharlaştırıcısına
100 kPa basınç ve 27oC sıcaklıkta 11.88 m3/dakika debiyle
girmektedir. Soğutucu akışkan-134a ise buharlaştırıcıya 140 kPa
basınçta, 0.3 kuruluk derecesiyle girmekte aynı basınçta doymuş
buhar olarak çıkmaktadır. Soğutucu akışkan-134a’nın debisi 1.81
kg/dakikadır. Her iki akış da süreklidir. 30ºC sıcaklıktaki çevre
ortamdan klima cihazına 33 kJ/dakika ısı geçişi olduğunu kabul
ederek (a) Havanın çıkış sıcaklığını, (b) birim zamandaki entropi
üretimini hesaplayınız. (Havayı mükemmel gaz ve özgül ısılarını
sabit kabul ediniz. Özgül ısıların oda sıcaklığındaki değerlerini
alınız.)
HAVA
& = 11.88 m3/dak
V
3
SA-134a
P1=140 kPa
x1= 0.3
x1= 0.3
T3= 27ºC
x2=1.0
T4= ?
Tçevre=30ºC
3
1
4
2
P2=140 kPa
x2= 1.0
P4=100 kPa
T4=?
(a) Açık Sistem (Kontrol Hacmi): Buharlaştırıcı (SASA)
Giriş Halleri: P1= 140 kPa,
P3= 100 kPa,
Çıkış Halleri: P2=140 kPa,
P4=100 kPa,
P3=100 kPa
T3=27°C
(SA-134a)
(Hava)
(SA-134a)
(Hava)
Soğutucu akışkan-134a Tablolarından,
h 1 = h f + x 1 h fg = 27.08 + (0.3) × (212.08) = 90.70 kJ / kg
P1 = 140 kPa
x 1 = 0.3
s1 = s f + x 1s fg = 0.11087 + (0.3) × (0.83368) = 0.36097 kJ / kg ⋅ K
P2 = 140 kPa h 2 = h g,140kPa = 239.16 kJ / kg
x 2 = 1.0
s 2 = s g,140kPa = 0.94456 kJ / kg ⋅ K
Hava mükemmel gaz kabul edilirse, girişteki havanın özgül hacmi:
RT3 0.287 × 300
=
= 0.861 m 3 / kg
P3
100
&
V
11.88
& hava = 3 =
m
= 13.8 kg / dakika (0.23 kg / s)
v 3 0.861
& ç = ∑m
&g
&2 =m
&1 =m
& SA
Kütlenin Korunumu: ∑ m
→ m
v3 =
ve
&4 =m
&3 =m
& hava
m
& = 33 kJ / dakika (0.55 kW )
Q
Kinetik ve potansiyel enerji değişimleri ihmal edilirse sürekli akışlı açık sistem için
Enerjinin Korunumu:
& −W
& Ê0 = ∑ m
& çhç − ∑ m
& ghg
Q
→
& = ∑m
& çhç − ∑ m
& ghg
Q
& = (m
& =m
& 2h 2 + m
& 4 h 4 ) − (m
& 1h 1 + m
& 3h 3 )
& SA (h 2 − h 1 ) + m
& hava (h 4 − h 3 )
Q
→
Q
& =m
& SA (h 2 − h 1 ) + m
& hava c po (T4 − T3 )
Havanın özgül ısıları sabit kabul edilirse,
Q
& −m
& SA (h 2 − h 1 )
Q
33 − 1.81 × (239.16 − 90.70 )
T4 = T3 +
= 27 o C +
= 10 o C
&
m hava c po
13.8 × 1.005
(b) Sadece çevresiyle ısı alışverişinde bulunan sürekli akışlı açık sistem için birim zamandaki entropi üretimi:
&
&
Q
Q
& çs ç − ∑ m
& g s g + çevre
& 4s 4 + m
& 2 s 2 ) − (m
& 3s 3 + m
& 1s1 ) + çevre
S& üretim = ∑ m
S& üretim = (m
⇒
Tçevre
Tçevre
&
Q
& SA (s 2 − s1 ) + m
& hava (s 4 − s 3 ) + çevre
S& üretim = m
Tçevre
T
P
Burada s 4 − s 3 = c po ln 4 − R ln 4
T3
P3
S& üretim
Ê0
T4
283
= 1.005 × ln
= −0.05863 kJ / kg ⋅ K
T3
300
− 33
= 1.81 × (0.94456 − 0.36097) + 13.8 × (−0.05863) +
303
= 0.1383 kJ / dakika ⋅ K = 0.0023 kW/K
= c po ln