11. sınıf konu anlatımlı - Nihat Bilgin Yayıncılık

11. SINIF
KONU ANLATIMLI
2. ÜNİTE: ELEKTRİK VE MANYETİZMA
4. Konu
MANYETİZMA
ETKİNLİK VE TEST ÇÖZÜMLERİ
4 Manyetizma
2
2. Ünite 4. Konu (Manyetizma)
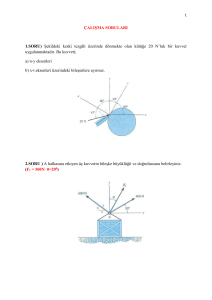
3. Üzerinden i akımı geen r yarıçaplı bir halkanın
merkezinde oluşan manyetik alanın büyüklüğü
A’nın Çözümleri
1.
P
B1
B2
2r i
B=K r
dir. Hem i1 hem de i2 akımı O noktasında 9 biçiminde manyetik alan oluşturur. Bileşke manyetik alan
için ikisini toplarız.
i1 = i
R
3B
r
B
i2 = 3i
r
O
i2 = 2i
S
B
3
3B
R noktasında bileşke manyetik alanın yönü 7 , S
noktasında bileşke manyetik alanın yönü 9 olur.
Nihat Bilgin Yayıncılık©
d
Y
6B 4B
6i
2d
X
3B
8B
d
8i
BX
BY
BX
BY
BX
BY
=
8-3
6+4
=
5
10
=
1
2
2d
i1 akımının O noktasında oluşturduğu manyetik alanın büyüklüğü;
2ri1
2ri
B1 = K r
= K· r
1
2ri
B1 = K r
B2 = K
2 · 2ri 1
·
2r
2
ri
B2 = K r
Çemberin merkezi olan O noktasında oluşan bileşke manyetik alanın büyüklüğü;
BO = B1 + B2
ri
2ri
BO = K r + K r
ri
BO = 3 K r olarak bulunur.
2.
i2
i1 = i
P noktasında bileşke manyetik alanın sıfır olması
için, ters yönlü B1 ve B2 alanlarının birbirine eşit olması gerekir. Bu durumda i1 = i ise i2 = 3i olur.
B1 B2
MANYETİZMA
4.
c. Sağ elin dört parmağı B 2 nin, başparmağı v nin
yönünü gösterecek şekilde elimizi ayarlarsak avuç
i2 = 2i
iX
3
içinden çıkılan dikme F nin yönünü gösterir. v ile
i1 = i
F birbirine dik olduğundan cismin yörüngesi şekildeki gibi daireseldir.
FZY
FXY
X
Y
Z
Üzerinden akım geçen tellerin birbirine uyguladığı
manyetik kuvvet;
2iX · i
d
·, = K
2i · 2i
·,
2d
iX = i
bulunur . (-)
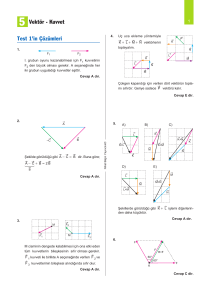
5. a. q yüklü parçacık v hızıyla B 1 manyetik alanından sapmadan geçmiştir. O hâlde, yüklü cisme
etkiyen elektrik ve manyetik kuvvetler eşit ve zıt
yönlüdür.
b. Yüklü parçacık v hızı ile levhalar arasında geçerken sapmadan geçiyorsa kendine etkiyen elektrik
ve manyetik kuvvetleri eşit ve zıt yönlüdür.
Fmanyetik
Felektrik = Fmanyetik
+q
FXY = FZY
K·
2i1 · i2
·,
d
bağıntısı ile hesaplanır. Ayrıca tellerden aynı yönde
akım geçiyorsa birbirini çeker. Zıt yönde akım geçiyorsa birbirini iter. Buradan;
F=K
Nihat Bilgin Yayıncılık©
F
qE = qvB 1
E
v=
B1
+q
Felektrik
v
v
4
Ünite 2
Elektrik ve Manyetizma
B’nin Çözümleri
4.
v2
|F2| = 0
v1
1.
–q
F1
i
+q
Şekil I
B
Şekil I deki manyetik alan sayfa düzlemindedir. Bu
alan içine v1 hızıyla atılan +q yüklü cisim sağ-el ku-
manyetik
alan çizgileri
i
ralına göre F 1 ( ) kuvvetinin etkisinde kalır. v2 hızıyla atılan –q yüklü cisim manyetik alan çizgilerine
i
paralel hareket ettiği için F 2 = 0 olur.
2.
F4
+q1
v2
v1
–q2
v4
F3
v1
Selenoidin ekseninde oluşan manyetik alan, şekildeki gibi düzgün bir alan olur. Bu alana paralel hareket eden yüklü cisimler, herhangi bir kuvvetin etkisinde kalmazlar. Manyetik alan içinde bu cisimlerin doğrultusu, yönü ve hızı değişmez.
Nihat Bilgin Yayıncılık©
v2
+q
–q
v3
Şekil II
Şekil II deki manyetik alan sayfa düzlemine dik olup
yönü içe doğrudur. Sağ-el kuralı uygulandığında
F 3 ve
olur.
F4
kuvvetlerinin yönü Şekil II deki gibi
3. Sağ elin başparmağı akımın yönünü (pozitif yüklerin hareket yönünü), dört parmak B nin yönünü gösterecek şekilde birbirine dik açılırsa, avuç içinden
çıkan dikme (+) yüklere etkiyen manyetik kuvvetin
yönünü gösterir.
+
–
anot
5.
i1 = i
katot
Şekil II
O hâlde (+) yüklü parçacıklara etkiyen kuvvet mıknatısın içine doğru olacaktır. Bir başka ifadeyle,
iyon demeti tüp içinde, mıknatısın iç kısmına doğru
sapar.
i3 = 2i
i2 = i
MANYETİZMA
C’nin Çözümleri
8. ( D )
9. ( D )
1. ( Y )
Mıknatıslar çevrelerinde manyetik alan oluşturabilir. Ayrıca üzerlerinden akım geçen iletkenlerin çevrelerinde de manyetik alan oluşur. Dünya’nın, diğer
gezegenlerin ve tüm gök cisimlerinin de bir manyetik alanı vardır.
10.( Y )
B
v
2. ( Y )
Manyetik alan çizgileri hem mıknatısın içinde, hem
de dışında vardır. Mıknatısın içinde manyetik alan
çizgileri S den N ye doğru, dışında ise N den S ye
doğrudur.
4. ( Y )
Hızı olmayan yüklü bir cisim manyetik alandan etkilenmez.
5. ( D )
6. ( D )
7. ( Y )
i
K·2i
d
d
d
30
°
B=
O
60°
K·2i
B= d
i
30°
d
B=
K·2i
d
Nihat Bilgin Yayıncılık©
3. ( D )
–q
5
Ünite 2
Elektrik ve Manyetizma
Test 1 in Çözümleri
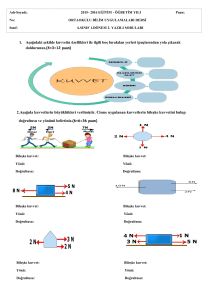
1. Arada yalıtkan varken X mıknatısı engele
2G . sin30° = G kadar bir etki yapar. Bu durumda T1
tepki kuvveti T1 = G dir. X ve Y mıknatısları arasındaki yalıtkan kaldırıldığında
yalıtkan
engel X N
S
T
α=30°
1
G
mıknatıslar birbirini F kuvvetiyle çeker.
T2
Y
N
S
F
Nihat Bilgin Yayıncılık©
6
K
F
G
N
S
G
α=30°
Hareket başladıktan sonra F kuvveti uzaklığın karesiyle ters orantılı olarak artar. Bu nedenle T1 azalır. Mıknatısların birbirine uyguladığı F çekme kuvveti arttıkça G ağırlıklı K cismin ivmesi artar. Bunun
sonucunda T2 ip gerilme kuvveti artar.
Yanıt A dır.
2. Sağ-el kuralını uygularsak, belirtilen noktalarda
manyetik alan vektörleri şekildeki gibi olur.
MANYETİZMA
K ve M noktalarında vektörler eşit ve zıt yönlü olduğundan bu noktalarda bileşke manyetik alan sıfır
olur. L ve N noktalarında ise vektörler aynı yönlü olduklarından, bu noktalardaki bileşke manyetik alan
sıfır olmaz.
5.
7
B2
B1
i1
d
i2 = 2i
d
i3 = 5i
d
d
B3
Yanıt C dir.
Düz telden geçen akımın, telin çevresinde oluşturduğu bileşke manyetik alanın büyüklüğü;
3. Sayfa düzleminde ve birbirine paralel iki telden, geçen akımlar aynı yönlü ise, bileşke manyetik alanın
sıfır olduğu nokta, teller arasındadır. i1 = i, i2= 3i olduğundan bileşke manyetik alan P noktasında sıfırdır.
2i
d
olup, yönü sağ-el kuralıyla bulunur. i2 akımının A
B tel = K
noktasında oluşturduğu B 2 manyetik alanın yönü
sayfa düzleminde ve yukarı doğrudur. B 2 nin büyüklüğü ise;
Yanıt D dir.
B2 = K
2i2
d
=K
2.2i
4i
=K
d
d
dir.
i3 akımının A noktasında oluşturduğu B 3 manyetik
alanın yönü sayfa düzleminde ve aşağı doğrudur.
B 3 ün büyüklüğü ise;
4.
Nihat Bilgin Yayıncılık©
i1
B1
A
i2
B
B 2 ve B 3 vektörleri ters yönlü olup büyüklük olarak
B3 > B2 dir. Bileşke manyetik alanın sıfır olabilmesi
i2 akımlarının A noktasında oluşturduğu B bileşke
=K
K
olur.
2i1
5i
4i
–K
=K
d
d
2d
i1 = i
Üzerinden akım geçen düz bir telin çevresindeki
manyetik alan şiddeti;
2i
d
bağıntısı ile, yönü ise sağ el kuralıyla bulunur. i1 ve
2d
için; B 1 vektörü B 2 ile aynı yönlü olmalıdır. Bunun
için i1 akımının yönü şekildeki gibi, büyüklüğü ise;
B tel = K
2.5i
5i
=K
2d
d
B3 = K
B2
2i3
6.
bulunur .
B1
iX
Yanıt C dır.
B2
FY
Z
iZ
manyetik alanın bileşenleri B 1 ve B 2 dir. B 1 in
büyüklüğü 2 birim, B 2 nin büyüklüğü ise 1 birimdir.
Buna göre;
B1 = 2 = K
B2 = 1 = K
2i1
2i2
2d
yazabiliriz. Bağıntıları taraf tarafa oranlarsak;
i1
i2
=3
bulunur .
Yanıt E dir.
Y
FZ
X
Şekil I
3d
iY
F
Şekil II
Sağ elin dört parmağı manyetik alanın yönünü, başparmak akımın yönünü gösterecek şekilde tutulursa, avuç içinden çıkılan dikme, tele etki eden manyetik kuvvetin yönünü gösterir. Bu yöntemle çözüm
yaptığımızda I, II ve III önermeleri doğru çıkar.
Yanıt E dir.
8
Ünite 2
Elektrik ve Manyetizma
7. Üzerinden akım geçen düz telin çevresinde oluşan
manyetik alan şiddeti:
B tel = K
8. Aynı yönlü akım taşıyan para-
K
L
lel iki tel, birbirine yaklaşacak
iL
iK
şekilde kuvvet uygular. O halde
2i
d
iK ile iL aynı yönlüdür. Zıt yönlü
FK
akım taşıyan paralel iki tel, bir-
FL
birinden uzaklaşacak biçimde
kuvvetin etkisinde kalır. Öyle
i1 = 4i
B3
B1
i2 = i
ise iX ile iY zıt yönlüdür. Üzerlerinden akım geçen paralel
B2
Y
iki telin birbirine uyguladığı
iX
manyetik kuvvetler eşit ve
i3
X
zıt yönlüdür.
bağıntısı ile bulunur. Üzerinden akım geçen iletken
çemberin merkezinde oluşan manyetik alan şiddeti
ise;
iY
FX
FY
İki tel arasındaki manyetik
kuvvetin büyüklüğü genel
2i1 .i2
2ri
B halka = K r
olarak;
bağıntısı ile bulunur. Sağ-el kuralına göre i1 ve i2
akımlarının çemberin merkezinde oluşturduğu
manyetik alanların yönü şekil üzerinde verildiği gibidir. Buna göre;
bağıntısıyla bulunur. Bu bağıntıya göre i1 ve i2
B1 = K
B2 = K
B2 = K
2i1
2d
4i
d
7
2.3.i
6i
=K
d
d
9
Yanıt A dır.
9. Manyetik alan içine, alan çizgilerine dik olarak atılan yüklü parçacık;
Fmanyetik = q v B
büyüklüğünde manyetik kuvvetin etkisinde kalır.
Manyetik kuvvet hız vektörüne dik uygulandığından, yüklü parçacık manyetik alan içinde düzgün
bulunur. B1 ve B2 zıt yönlü olup B2 > B1 dir. O noktasında bileşke manyetik alanın sıfır olabilmesi için;
B3 manyetik alanın yönü
biçiminde olmalıdır.
Bunun için i3 akımı (2) yönünde akmalıdır. i3 akımının şiddeti ise;
B1 + B3 = B2
K
2i3
d
=K
i3 = i
.,
de seçeneklerin içinde yanlış olan A seçeneğidir.
2ri2
d
d
akımları eşit olabileceği gibi farklı da olabilir. O halNihat Bilgin Yayıncılık©
B1 = K
F=K
dairesel hareket yapar. Parçacığın düzgün dairesel
hareket yapmasını sağlayan merkezcil kuvvet;
Fmerkezcil =
mv 2
r
dir. Manyetik ve merkezcil kuvvetler aynı kuvvet olduğundan;
6i
4i
-K
d
d
q v B=
bulunur .
r=
Yanıt C dir.
mv 2
r
mv
qB
bulunur. Bulduğumuz son bağıntıya göre yörünge
yarıçapını büyütmek için q ile B yi küçültmek gerekir.
Yanıt B dir
MANYETİZMA
10.9. sorunun çözümünü yaparken yörünge yarıçapını;
mv
qB
olarak bulmuştuk. Bağıntıya göre r nin iki katına
çıkması için v nin iki katına çıkması gerekir.
Öte yandan, –q yüklü parçacık K levhasından L levhasına giderken elektrik kuvvetleri,
W = q VH
kadar iş yapar. Yapılan bu iş cismin kinetik enerjisini artırır. Buradan;
qVH =
FY = i . Btop . l . sinα
dır. Manyetik alan tele dik uygulandığından;
FY = i Y . ( B +
FY = 2 i .
v=
B
).,
2
3
B . , = 3 Bi ,
2
1
mv 2
2
12.Tellerin dışındaki A noktasında bileşke manyetik
alanın sıfır olabilmesi için i1 ve i2 akımlarının şekildeki gibi ters yönde akması gerekir. Ayrıca manyetik alan şiddeti uzaklıkla ters orantılı olduğundan
i2 = 2i dir.
2 qVH
m
yazabiliriz. Buna göre v nin 2 katına çıkması için
VH , 4 katına çıkarılmalıdır.
A
B1
Yanıt C dir.
iX = i
iY = 2i
B
BY
B2
d
Nihat Bilgin Yayıncılık©
11.
bulunur .
Yanıt D dir.
r=
i1 = i
d
i2
i2 = 2i
(1)
Yanıt A dır.
B
B
BX =
2
13.
X teli üzerinde zıt yönde (BY ve B ) olan manyetik alanlar birbirinin etkisini sıfırladığı için FX = 0 olarak verilmiştir. Buradan BY = B olduğunu söyleyebiliriz.
BY = K
2.2i
= B ise
d
BX = K
2.i
B
=
d
2
3
B
= B
2
2
olur. Y teline etki eden bileşke kuvvet;
B + BX = B +
B3
B1
olur .
Y teli üzerindeki B ve BX manyetik alanları aynı yönlü olduğundan, bileşke için ikisini toplarız. Y teline
etki eden bileşke manyetik alan;
9
B2
i3 = i akımının A noktasında oluşturduğu manyetik
alan şiddeti;
2i
=9 B
d
olarak verilmiştir. i1 akımının A noktasında oluşturduğu manyetik alan şiddeti;
B3 = K
10
Ünite 2
B1 = K
2i
2d
i
B1 = K d
olur. i2 akımının A noktasında oluşturduğu manyetik
alan şiddeti;
B2 = K
2.2i
4i
=K
d
d
BA = 7
bulunur. Bu iki kuvvet zıt yönlü olduğundan;
FR = 3F – 2F = F
ve (2) yönündedir. Yön de dikkate alındığında
FR = F bulunur.
3
B
2
bulunur .
Yanıt C dir
2.i1 .i2
.l
d
bağıntısı ile hesaplanır. Tellerin uzunlukları eşit olduğundan oluşan manyetik kuvvet, akımlar ve teller arası uzaklığa bağlı olarak değişir. Ayrıca tellerden aynı yönde akım geçerken çekme, zıt yönlerde
akım geçerken itme kuvveti oluşur.
F=K
15.Sağ elin başparmağı akımın
yönünü gösterecek şekilde
düz tel avuç içine alınırsa, telden geçen akımın O noktasında oluşturduğu manyetik
alanın yönü sayfa düzlemine dik ve yönü okuyucuya doğrudur. Ayrıca halkadan geçen akımın, halka
merkezinde oluşturduğu manyetik alan da sayfa
düzlemine dik ve yönü okuyucuya doğru olur.
(1)
(2)
Halka merkezinde oluşan toplam manyetik alan şiddeti;
B top =
FRP = K
2 . i . 2 i . = 2 F olur .
l
d
FP = FSP + FRP = 3 F
bulunur .
→
B1 +
→
B2 ile bulunur.
2i1
2 ( 3i )
6i
B1 = K r = K r = K r
P teline etkiyen kuvvetler;
B2 = K
2.i.3i .
FSP = K
l = F ise
3d
2.2i.3i .
l = 3F
2d
B
+72 B
2
14.Üzerinden akım geçen tellerin birbirine uyguladığı
manyetik kuvvetin büyüklüğü;
FSR = K
Yanıt C dir
Nihat Bilgin Yayıncılık©
2.i.2i .
l = 2F
d
bulunur. A noktasındaki bileşke manyetik alan;
BA = 9 B + 7
FPR = K
B2 = 7 2 B
P teline etki eden net kuvvet (2) yönünde ve 3F büyüklüğünde olur. R teline etkiyen kuvvetler;
B
2
B1 = 7
Elektrik ve Manyetizma
2ri2
2 ( 3i )
6i
r =K r =K r
değerleri yerine konulursa;
12 i
B top = K r 9 bulunur.
MANYETİZMA
Yanıt D dir
16.Düzgün manyetik alanı içinde çembersel hareket
yapan bir cisim için yarıçap bağıntısı;
mv
qB
r=
idi. r yörünge yarıçapı biliniyor, q yu bulabilmek için
mv ile B yi de bilmek gerekir.
Nihat Bilgin Yayıncılık©
Yanıt C dir.
11