EME 3105 SİSTEM SİMÜLASYONU

12.12.2013
1
EME 3105
SİSTEM SİMÜLASYONU
Rassal Değer Üretimi
Ders 11
Amaç
• Bir simulasyon modelinde girdi olarak
kullanılmak üzere belirli bir dağılımdan
örneklem üretilmesi
• Yaygın olarak kullanılan rassal değer üretim
yöntemlerinin öğrenilmesi


Ters dönüşüm tekniği
Kabul-ret tekniği
2
Dağılımlardan Örneklem Alınması
Rassal Değer Üretme Teknikleri
• Tahmin edilemeyen yada belirsiz faaliyetlerin
modellenmesinde istatistiksel dağılımlar kullanılır.
• Rassal değer üretme tekniklerinin tümü [0,1]
aralığında Düzgün dağılmış rassal sayıların elimizde
mevcut olduğunu varsayar.
• Gerçek yaşam problemlerindeki gelişler arası süre,
servis süreleri, talep vb. değişkenler genellikle
tahmin edilemezdir.
Her bir Ri rassal sayı için:
• Bu tür değişkenler, belli bir istatistiksel dağılıma
sahip rassal değişkenler olarak modellenebilir.
1
12.12.2013
Ters Dönüşüm Tekniği
Ters Dönüsüm Tekniği (Devam)
Üstel, Düzgün, Weibull ve deneysel sürekli
dağılımların yanı sıra bir çok kesikli dağılımdan
örneklem almaya uygun bir yöntemdir.
• Tekniğin temel mantığı:
r = F(x) birikimli dağılım fonksiyonu için
[0,1] düzgün dağılımından r rassal sayısını üret
 x’i hesapla.


F(x)
r = F(x)
Hesaplama yönünden basit ve direk bir yöntem
x=
F-1(r)
r1
olmasına karşın, her zaman etkin değildir.
x1
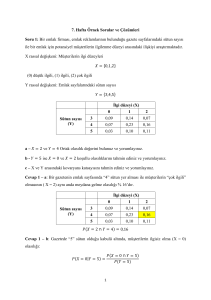
Deneysel Kesikli Dağılım
Deneysel Kesikli Dağılım (Devam)
(Ters Dönüşüm)
(Ters Dönüşüm)
R
xi
1
2
3
f xi  0.4 0.3 0.2
0.4 0.7 0.9
F x i 
if x  1
0
0.4 if 1  x  2

F ( x)  0.7 if 2  x  3
0.9 if 3  x  4

 1
if 4  x
4
1.0
X=4 (0.9 < R ≤ 1)
0.1
1.0
.8
X=3 (0.7 < R ≤ 0.9)
.6
Eğer Ri aralıktaysa
0 £ Ri £ 0.4
0.4 < Ri £ 0.7
0.7 < Ri £ 0.9
0.9 < Ri £ 1.0
Xi
1
2
3
4
X=2 (0.4 < R ≤ 0.7)
.4
X=1 (0 ≤ R ≤ 0.4)
.2
0
Kesikli Ters Dönüşüm Algoritması
Üret ri = uniform(0,1)
for i=1 to n
If ri £ F(xi ) then return x
Loop
i
0
1
2
3
x
4
2
12.12.2013
[a,b] Aralığında Düzgün Değer Üretimi
Uygulamalar
(Ters Dönüşüm)
• Düzgün dağılmış X rassal değişkenine ait f(x) olasılık
yoğunluk fonksiyonu aşağıda verilmiştir.
• [a,b] aralığında Düzgün Değer Üretimi
ì 1
ï
f(x) = í b - a
ïî0
• Üstel Değer Üretimi
[a,b] Aralığında Düzgün Değer Üretimi (Devam)
(Ters Dönüşüm)
• X rassal değişkeninin Birikimli Dağılım Fonksiyonu
F(x), Olasılık Yoğunluk Fonksiyonu f(x)’in integrali
alınarak bulunur.
F(x) = ò
Aksi Halde
f(x): Olasılık Yoğunluk Fonksiyonu (Probability density function, pdf):
9
ì0
ïï x - a
f(x)dx = í
ïb - a
ïî1
a£ x£b
[a,b] Aralığında Düzgün Değer Üretimi
(Devam)
(Ters Dönüşüm)
• Düzgün dağılımdan değerler üretmede ters dönüşüm
metodunu kullanmak için Fx(x) = R alınır ve x aşağıdaki
gibi çözülür:
x- a
= RÞ x = F -1 (x) = (b - a) ´ R+ a
b- a
x<a
a£ x£b
x>b
• Artık, [a,b] aralığında Düzgün rassal değer üretebiliriz:
 [0,1] aralığında Düzgün R üret
 x = a + R (b -a)
F(x): Birikimli (Olasılık) Dağılım Fonksiyonu (Cumulative density function, cdf)
12
3
12.12.2013
Üstel Dağılım (Devam)
Üstel Dağılım (Ters Dönüşüm)
13
(Ters Dönüşüm)
14
ìl e- l x
f (x) = í
î0
ì0
F(x) = í
-lx
î1- e
E[X] =
1
l
x³0
1- İstenilen X rassal değişkeni için kümülatif yoğunluk
fonksiyonu hesaplanır.
A ksi Halde
x<0
0 £ x£¥
l=
1
E[X]
Üstel Dağılım (Devam)
Üstel Dağılım (Devam)
(Ters Dönüşüm)
15
(Ters Dönüşüm)
16
4
12.12.2013
Üstel Dağılım (Devam)
Üstel Dağılım (Devam)
(Ters Dönüşüm)
(Ters Dönüşüm)
17
18
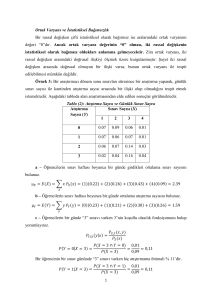
Rassal Normal Değer Üretme
Rassal Normal Değer Üretme
(0,5<Rassal Sayı<1)
(0,5<Rassal Sayı<1)

r = F(x) birikimli dağılım fonksiyonu için

[0,1] düzgün dağılımından r rassal sayısını üret

x’i hesapla.
P( Z £ 1, 4 ) = 0,919
z = 1, 4
z
s = 100
2
Örnegin m =25,s 2 = 100 parametreli
Normal Dagilimdan rassal deger uretelim.
R=0.919 olsun.
F(x) = 0,919
m = 25
f(z)
x
z=
x = m + zs
x = m + zs
= 25 + 1, 4.10
= 39
x- m
s
F(z) = 0,919
z
5
12.12.2013
Rassal Normal Değer Üretme
Rassal Normal Değer Üretme
(0<Rassal Sayı<0,5)
(0<Rassal Sayı<0,5)
Üretilen rassal sayının 0.5’ten küçük olması normal dağılımdan üretilecek
değerin ortalamadan küçük olduğunu gösterir.
s 2 = 100
s2 =1
Örnegin m =25,s 2 = 100 parametreli
Normal Dagılımdan rassal deger uretelim.
R=0.35 olsun.
-z
m = 25
x
z=
s
P(Z < -z) = P(Z > z) = 0, 35
s =1
2
F(z) = RS = 0,35
-z
0
Rassal Normal Değer Üretme
(0<Rassal Sayı<0,5)
P( Z £ 0.39 ) = 0,65
f(z)
P(Z £ -0.39) = 0, 35
z = 0, 39
z
Þ
0
x- m
F(x) = RS = 0, 35
x = m - zs
0
s2 =1
z
x = m - zs
= 25 - 0, 39.10
= 21,1
6
P(Z < z) = 1- 0, 35
= 0,65
z
0, 35