7. Hafta Örnek Sorular ve Çözümleri Soru 1: Bir emlak

7. Hafta Örnek Sorular ve Çözümleri
Soru 1: Bir emlak firması, emlak reklamlarının bulunduğu gazete sayfalarındaki sütun sayısı
ile bir emlak için potansiyel müşterilerin ilgilenme düzeyi arasındaki ilişkiyi araştırmaktadır.
X rassal değişkeni: Müşterilerin ilgi düzeyleri
𝑋 = 0,1,2
(0) düşük ilgili, (1) ilgili, (2) çok ilgili
Y rassal değişkeni: Emlak sayfalarındaki sütun sayısı
𝑌 = 3,4,5
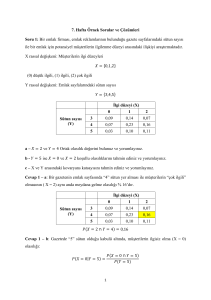
İlgi düzeyi (X)
Sütun sayısı
(Y)
0
1
2
3
0,09
0,14
0,07
4
0,07
0,23
0,16
5
0,03
0,10
0,11
a – 𝑋 = 2 ve 𝑌 = 4 Ortak olasılık değerini bulunuz ve yorumlayınız.
b - 𝑌 = 5 ise 𝑋 = 0 ve 𝑋 = 2 koşullu olasılıklarını tahmin ediniz ve yorumlayınız.
c – X ve Y arasındaki kovaryans katsayısını tahmin ediniz ve yorumlayınız.
Cevap 1 – a: Bir gazetenin emlak sayfasında “4” sütun yer alması ile müşterilerin “çok ilgili”
olmasının ( X = 2) aynı anda meydana gelme olasılığı % 16’dır.
İlgi düzeyi (X)
Sütun sayısı
(Y)
0
1
2
3
0,09
0,14
0,07
4
0,07
0,23
0,16
5
0,03
0,10
0,11
𝑃 𝑋 = 2 ∩ 𝑌 = 4 = 0,16
Cevap 1 – b: Gazetede “5” sütun olduğu kabulü altında, müşterilerin ilgisiz olma (X = 0)
olasılığı:
𝑃 𝑋=0𝑌=5 =
𝑃 𝑋 =0∩𝑌 =5
𝑃(𝑌 = 5)
1 𝑃 𝑋 = 0 ∩ 𝑌 = 5 = 0,03
İlgi düzeyi (X)
Sütun sayısı
(Y)
𝑃 𝑌=5 =
0
1
2
3
0,09
0,14
0,07
4
0,07
0,23
0,16
5
0,03
0,10
0,11
𝑃 𝑥, 𝑦 = 𝑃 𝑌 = 5 ∩ 𝑋 = 0 + 𝑃 𝑌 = 5 ∩ 𝑋 = 1 + 𝑃 𝑌 = 5 ∩ 𝑋 = 2
!
𝑃 𝑌 = 5 = 0,03 + 0,10 + 0,11
𝑃 𝑌 = 5 = 0,24
İlgi düzeyi (X)
Sütun sayısı
(Y)
0
1
2
3
0,09
0,14
0,07
4
0,07
0,23
0,16
5
0,03
0,10
0,11
𝑃 𝑋=0𝑌=5 =
Y değişkeninin “5” değerini alma olasılığı (Kenar veya Marjinal olasılık) 0,24 𝑃 𝑋 =0∩𝑌 =5
0,03
=
= 0,125
𝑃(𝑌 = 5)
0,24
Gazetelerin emlak sayfasında “5” sütun olduğu durumda müşterilerin ilgisiz olma olasılığı %
12.5’tir.
Gazetede “5” sütun olduğu kabulü altında, müşterilerin çok ilgili olma (X = 2) olasılığı:
𝑃 𝑋=2𝑌=5 =
𝑃 𝑋 =2∩𝑌 =5
𝑃 𝑌=5
𝑃 𝑋 = 0 ∩ 𝑌 = 5 = 0,11
İlgi düzeyi (X)
Sütun sayısı
(Y)
𝑃 𝑋=2𝑌=5 =
0
1
2
3
0,09
0,14
0,07
4
0,07
0,23
0,16
5
0,03
0,10
0,11
𝑃 𝑋 =2∩𝑌 =5
0,11
=
= 0,4583
𝑃 𝑌=5
0,24
Gazetelerin emlak sayfasında “5” sütun olduğu durumda müşterilerin çok ilgili olma olasılığı
% 45.83’tür.
2 Cevap 1 – c:
𝐶𝑂𝑉 𝑋, 𝑌 = 𝐸 𝑋𝑌 − 𝐸 𝑋 𝐸(𝑌)
Öncelikle rassal değişkenlerin beklenen değerleri (ortalamaları) hesaplanır:
𝐸 𝑋 =
𝑥𝑃(𝑥, 𝑦)
X rassal değişkeninin her bir değeri için kenar/marjinal olasılıklar hesaplanır:
𝑃 𝑋=𝑥 =
𝑃(𝑥, 𝑦)
!
𝑃 𝑋 =0 =𝑃 𝑋 =0∩𝑌 =3 +𝑃 𝑋 =0∩𝑌 =4 +𝑃 𝑋 =0∩𝑌 =5
𝑃 𝑋 = 0 = 0,09 + 0,07 + 0,03 = 0,19
Rassal olarak seçilen birinin ilgi düzeyinin “0” olma olasılığı % 19’dur.
𝑃 𝑋 =1 =𝑃 𝑋 =1∩𝑌 =3 +𝑃 𝑋 =1∩𝑌 =4 +𝑃 𝑋 =1∩𝑌 =5
𝑃 𝑋 = 1 = 0,14 + 0,23 + 0,10 = 0,47
Rassal olarak seçilen birinin ilgi düzeyinin “1” olma olasılığı % 47’dir.
𝑃 𝑋 =2 =𝑃 𝑋 =2∩𝑌 =3 +𝑃 𝑋 =2∩𝑌 =4 +𝑃 𝑋 =2∩𝑌 =5
𝑃 𝑋 = 2 = 0,07 + 0,16 + 0,11 = 0,34
Rassal olarak seçilen birinin ilgi düzeyinin “1” olma olasılığı % 34’tür.
𝐸 𝑋 =
𝑥𝑃 𝑥, 𝑦 = 0×𝑃 𝑋 = 0 + 1×𝑃 𝑋 = 1 + 2×𝑃 𝑋 = 2
𝐸 𝑋 = 0 0.19 + 1 0,47 + 2 (0,34)
𝐸 𝑋 = 1.15
Bu veri setinde yer alan kişilerin ortalama ilgi düzeyi 1.15’tir.
𝐸 𝑌 =
𝑦𝑃(𝑥, 𝑦)
Y rassal değişkeninin her bir değeri için kenar/marjinal olasılıklar hesaplanır:
𝑃 𝑌=𝑦 =
𝑃(𝑥, 𝑦)
!
𝑃 𝑌 =3 =𝑃 𝑋 =0∩𝑌 =3 +𝑃 𝑋 =1∩𝑌 =3 +𝑃 𝑋 =2∩𝑌 =3
3 𝑃 𝑌 = 3 = 0,09 + 0,14 + 0,07 = 0,30
Rassal olarak seçilen bir gazete sayfasının “3” sütunlu olma olasılığı % 30’dur.
𝑃 𝑌 =4 =𝑃 𝑋 =0∩𝑌 =4 +𝑃 𝑋 =1∩𝑌 =4 +𝑃 𝑋 =2∩𝑌 =4
𝑃 𝑌 = 4 = 0,07 + 0,23 + 0,16 = 0,46
Rassal olarak seçilen bir gazete sayfasının “4” sütunlu olma olasılığı % 46’dır.
𝑃 𝑌 =5 =𝑃 𝑋 =0∩𝑌 =5 +𝑃 𝑋 =1∩𝑌 =5 +𝑃 𝑋 =2∩𝑌 =5
𝑃 𝑌 = 5 = 0,03 + 0,10 + 0,11 = 0,24
Rassal olarak seçilen bir gazete sayfasının “5” sütunlu olma olasılığı % 24’tür.
𝐸 𝑌 =
𝑦𝑃 𝑥, 𝑦 = 3×𝑃 𝑌 = 3 + 4×𝑃 𝑌 = 4 + 5×𝑃 𝑌 = 5
𝐸 𝑌 = 3 0.30 + 4 0,46 + 5 (0,24)
𝐸 𝑌 = 3.94
Bu veri setinde yer alan gazetelerin emlak sayfalarındaki ortalama sütun sayısı 3.94’tür.
Ortak varyansın hesaplanabilmesi için şimdi de ortak dağılımın beklenen değerini
hesaplayalım:
𝐸 𝑋𝑌 =
𝑥𝑦𝑃 𝑥, 𝑦 = 0 3 ( 0,09) + 0 4 0,07 + 0 5 0,03
+ 1 3 0,14 + 1 4 0,23 + 1 5 0,10 + 2 3 0,07
+ 2 4 0,16 + 2 5 0,11 = 4,64
𝐶𝑂𝑉 𝑋, 𝑌 = 𝐸 𝑋𝑌 − 𝐸 𝑋 𝐸 𝑌 = 4,64 − 1,15 3,94
= 0,109
Ortak varyans değerinin “0” olmaması, bu iki değişken arasında doğrusal bir ilişkinin
varlığını göstermektedir. Kovaryans değerinin pozitif olması, bu iki değişken arasında pozitif
yönlü (doğrusal) bir ilişkinin varlığına işarettir.
4 Soru 2: 20 üst düzey yöneticiye bir konferans için davetiye gönderilmiştir. Her bir
yöneticinin bu daveti kabul etme olasılığı 0.90 olarak belirlenmiştir. Her bir yönetici
birbirinden bağımsız olarak katılım kararını verdiği kabul edilmektedir.
a – Bu konferansa 16 yönetici katılma olasılığı nedir?
b – Bu konferansa 17 yönetici katılma olasılığı nedir?
c – Bu konferansa en fazla 18 yönetici katılma olasılığı nedir?
Cevap 2 – a:
𝑃 𝑋 = 16 =?
𝑛 = 20
𝑝 = 0.90
Elimizdeki veriler, değişkenin (yöneticilerin toplantıya katılma kararı) iki terimli bir olasılık
dağılımına sahip olduğunu göstermektedir (Yöneticilerin katılma veya katılmama kararı
verecek olmaları).
𝑃 𝑋=𝑥 =
𝑃 𝑋 = 16 =
𝑛!
𝑝 ! (1 − 𝑝)!!!
𝑥! 𝑛 − 𝑥 !
20!
0,9
16! 20 − 16 !
!"
(0,1)! = 0,08977
Davet edilen 20 yönetici arasından 16 yönetici katılma olasılığı % 8.97’dir.
Cevap 2 – b:
𝑃 𝑋 = 17 =?
𝑛 = 20
𝑝 = 0.90
𝑃 𝑋=𝑥 =
𝑃 𝑋 = 17 =
𝑛!
𝑝 ! (1 − 𝑝)!!!
𝑥! 𝑛 − 𝑥 !
20!
0,9
17! 20 − 17 !
!"
(0,1)! = 0,1901
Davet edilen 20 yönetici arasından 17 yönetici katılma olasılığı % 19,01’dir.
5 Cevap 2 – c: “En fazla 18 yönetici” katılma olasılığı demek, 0 ile 18 arasındaki bütün katılma
sayılarının olasılıklarının hesaplaması demektir.
𝑃 𝑋 ≤ 18 =?
Bu olasılık, şu şekilde de bulunabilir:
𝑃 𝑋 ≤ 18 = 1 − 𝑃 𝑋 = 19 + 𝑃(𝑋 = 20)
Şayet 19 ve 20 yönetici katılma olasılıklarını ayrı ayrı bulup, toplamlarını “1” değerinden
çıkartırsak bu, aynı zamanda katılımcı sayısının 18 ve daha düşük olma olasılığına da eşit
olacaktır.
𝑃 𝑋 = 19 =
20!
0.90
19! 20 − 19 !
!"
(0.10)!"!!" = 0,2701
𝑃 𝑋 = 20 =
20!
0.90
20! 20 − 20 !
!"
(0.10)!"!!" = 0,1215
𝑃 𝑋 ≤ 18 = 1 − [ 0,2701 + (0,1215)]
𝑃 𝑋 ≤ 18 = 0,6084
Bu toplantıya en fazla 18 yönetici katılma olasılığı %60,84’tür.
6 Soru 3: Bir araç satım firmasında işe başlamayı düşünüyorsunuz. Bu iş yerinde bir hafta
içerisinde satılan araç sayısı ve bu sayıda araç satma olasılıkları aşağıdaki gibidir:
Araç sayısı
0
1
2
3
4
5
Olasılık
0,10
0,20
0,35
0,16
0,12
0,07
a – Bir haftada beklenen araç satışı ve standart sapmasını hesaplayınız.
X rassal değişkeni: Satılan araç sayısı
𝑋 = 0,1,2,3,4,5
Bu rassal değişkenin ortalaması:
𝐸 𝑋 =
𝑥𝑃(𝑋 = 𝑥)
𝐸 𝑋 = 0 0,1 + 1 0,2 + 2 0,35 + 3 0,16 + 4 0,12 + 5 0,07
𝐸 𝑋 = 2.21
Bu firmada çalışan birinin haftalık ortalama araç satışı 2.21 olacaktır.
𝑥 ! 𝑃 𝑋 = 𝑥 − 𝐸(𝑋)
𝑠𝑑 𝑋 =
𝑥 !𝑃 𝑋 = 𝑥 = 0
!
0,1 + 1
!
0,2 + 2
𝑠𝑑 𝑋 =
!
0,35 + 3
!
!
0,16 + 4
!
0,12 + 5
!
0,07
6,71 − (2.21)! = 1.82
Haftalık araç satışındaki ortalama değişkenlik, 1.82 araç olacaktır.
b – Bu işyerinde çalışmanız durumunda haftalık sabit 250 TL ve sattığınız her araç başına 300
TL verilecektir. Haftalık ortalama kazancınız ne kadar olacaktır?
𝐻𝑎𝑓𝑡𝑎𝑙ı𝑘 Ü𝑐𝑟𝑒𝑡 = 𝑠𝑎𝑏𝑖𝑡 ü𝑐𝑟𝑒𝑡 + 𝑎𝑟𝑎ç 𝑏𝑎şı ö𝑑𝑒𝑚𝑒 ×(𝑎𝑟𝑎ç 𝑠𝑎𝑦ı𝑠ı)
𝑊 = 250 + 300𝑋
Ortalama haftalık kazanç:
𝐸 𝑊 = 250 + 300𝐸(𝑋)
𝐸 𝑊 = 250 + 300×2.21 = 913
7 Haftalık ortalama kazancının 913 TL olması beklenir.
c – Bu işyerinde çalışırsanız haftalık ücretinizin 850 TL ve daha az olma olasılığı nedir?
0 ≤ 𝑊 ≤ 850 𝑇𝐿 𝑜𝑙𝑚𝑎𝑠ı 𝑖ç𝑖𝑛 𝑋 ≤ 2 𝑜𝑙𝑚𝑎𝑙ı𝑑ı𝑟
𝑃 𝑋 ≤ = 1 − 𝑃 𝑋 = 3 + 𝑃 𝑋 = 4 + 𝑃(𝑋 = 5)
𝑃 𝑋 ≤ 2 = 1 − [ 0,16 + 0,12 + (0,07)]
𝑃 𝑋 ≤ 2 = 0,65
Bu işyerinde çalışmayı kabul ederseniz haftalık ücretinizin 850 TL ve daha düşük olma
olasılığı % 65’tir.
8