dosyayı indir

TRİGONOMETRİ − 2
TRİGONOMETRİK FONKSİYONLAR
TRİGONOMETRİK FONKSİYONLAR
BİR AÇININ KOSİNÜS VE SİNÜS DEĞERLERİ
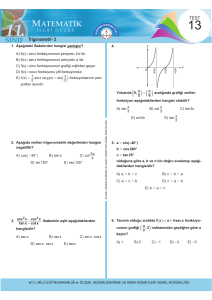
Örnek...1 :
B i r i m ç e m b e r k u l l a n a r ak a ş a ğ ı d ak i i f a d e l e r i
h e s a p l a yı n ı z.
Sinüs
ekseni
M e r k e zi
orijin ve
ya r ı ç a p ı 1
P(a,b)
birim olan
çembere
1
birim çember
x
Kosinüs
d e n i r.
Standart
ekseni
O
p o zi s yo n d a
(Köşesi
orijinde,
başlangıç
y
k en a r ı x
ekseni ve
yö n ü p o zi t i f yö n o l a n a ç ı ) v e ö l ç ü s ü θ
o l a n a ç ı n ı n b i r im ç em b e r ü ze r i n d e ya y
bitim noktası P(a,b) olsun:
y
a) sin 900
b) cos 1800
B 1
C
−1
O
A
1
x
−1 D
c) sin 225
d) cos 3300
0
1, -1,
−√ 2
,
2
√3
2
θ r e e l s a yı s ı n ı c o s θ i l e e ş l e ye n
f on k s i yo n a k o s i n ü s f o n k s i yo n u d e n i r.
K o s i n ü s F o nk s i yo n u
cos : R → [−1,1]
θ → cos θ
Burada cos θ nın değer aralığı
−1≤ cos θ ≤1 d i r.
A yr ı c a , c o s ( θ + k . 2 π )= c o s θ d ı r.
www.matbaz.com
˙
A ) cos(θ)=a
o l a r a k t a n ı m l a n ı r.
O x e k s e n i n e k o s i n ü s ek s e n i d e n i r.
Örnek...2 :
sin2 12+cos 2 12−1
sin 67+cos 34. sin41
i ş l e m i n i n s o n u c u k a ç t ır ?
0
B ) sin(θ)=b o l a r a k t a n ı m l a n ı r.
O y e k s e n i n e i s e s i n ü s ek s e n i d e n i r
θ r e e l s a yı s ı n ı s i n θ i l e e ş l e ye n
f on k s i yo n a s i n ü s f o n k s i yo n u d e n i r
S i n ü s F o n k s i yo n u
sin : R → [−1,1]
θ → sin θ
Burada sin θ nın değer aralığı
−1≤ sinθ ≤1 d i r.
A yr ı c a , s i n ( θ + k . 2 π )= s i n θ
Örnek...3 :
13+5 sinx
3
i s e a k a ç f a rk l ı t am s a yı d e ğ e r i a l ır ?
a=
4
d ı r.
SONUÇ
O K P d ik ü ç g e n i n d e cos 2(θ)+sin2 (θ)=1 d i r.
11.
11. Sınıf Matematik Konu Anlatımı
1/6
TRİGONOMETRİ − 2
TRİGONOMETRİK FONKSİYONLAR
BİR AÇININ TANJANT VE KOTANJANT
DEĞERLERİ
Birim
çembere
A(1,0)
Kotanjant
ekseni
DAR AÇILARIN TRİGONOMETRİK
DEĞERLERİ
y
)
k,1
K(
B 1
y
K
T(1,t)
tanθ
1
x
sinθ
O cos P
1
Tanjant
ekseni
A
1
F
R
x
T
n o k t a s ı n d a n ç i zi l e n t e ğ e t e t a n j a n t
e k s e n i , B ( 0 , 1 ) n ok t a s ı n d a n ç i zi l e n t e ğ e t e
d e k o t a n j a n t e k s e n i d e n i r.
P O R d ik ü ç g e n i n d e cos 2(θ)+sin2 (θ)=1 e l d e
edilir
B i r a ç ı n ı n t a n j a n t (k o t a n j a n t ) d e ğ e r i
b u l u n u r k e n ş u a d ı m l a r i zl e n i r :
Ş ek i l d ek i P O R v e TO F ü ç g e n l e r i n i n
benzerliğinden
A d ı m 1 ) Ve r i l e n a ç ı ya e ş i t o l a n p o zi t if
yö n l ü s t a n d a r t b i ç im l i ya y ı n b i t i m n o k t a s ı
b i r i m ç e m b e r d e i ş a r e t l e n i r,
sin (θ)
ve
cos(θ)
cos(θ)
cot(θ)=
sin(θ)
e l d e e d i l i r.
A d ı m 2 ) Ya y b i t i m n o k t a s ı v e o r i j i n i
b i r l e ş t i r e n d o ğ r u ç i zi l i r,
A d ı m 3 ) D o ğ r u t a n j a n t ek s e n i i l e
k es i ş t i r i l i r,
A d ı m 4 ) K e s i m n o k t a s ı n ı n o r d i n a t ı a ç ın ı n
t a n j a n t ı d ı r.
A yn ı ş ek i l d e k o t a n j a n t d e ğ e r i d e ya y
b i t i m v e o r i j i n i b i r l e ş t i r e n d o ğ r u n u n ( v e ya
u za n t ı s ı n ı n ) k o t a n j a n t e k s e n i n i k e s t i ğ i
n o k t a n ı n a p s i s i d i r.
Örnek...4 :
B i r im ç em b e r k ul l a n a r a k a ş a ğ ı d a k i if a d e l e r i
h e s a p l a yı n ı z .
a) tan 60
b) cot 210
c) tan 225
www.matbaz.com
tan (θ)=
Z
r
y
Bu benzerliğin
M
x
r a s t g e l e b e n ze r
b i r d ik ü ç g e n e u yg u l a n m a s ı yl a
T
x
y
y
x
, sin(θ)=
, tan (θ)= , cot(θ)=
r
r
x
y
e l d e e d i l i r.
cos(θ)=
TRİGONOMETRİK ÖZDEŞLİKLER
cos2 (θ)+sin2 (θ)=1
v e tan(θ).cot(θ)=1 d i r.
Ayr ı c a b i r b i r i n i 9 0 o ye ( π ye )
2
t am am l a ya n a ç ıl a r i ç i n
birinin sinüsü diğerinin kosinüsüne ;
birinin tanjantı diğerinin kotanjantına
e ş i t t i r. Ya n i ,
y
x
cos(90 o−θ)= =sin(θ) , tan(90o −θ)= =cot (θ)
r
y
y
B 1
C
−1
O
A
1
x
Örnek...5 :
5 sinx
cosx
i s e t a n x k a ç t ır ?
=
9
tanx . cotx+2
−1 D
√3 , √3 ,
11.
11. Sınıf Matematik Konu Anlatımı
3
5
1
2/6
TRİGONOMETRİ − 2
TRİGONOMETRİK FONKSİYONLAR
SEKANT VE KOSEKANT FONKSİYONLARI :
Örnek...6 :
c o s 2 1 o + c o s 2 2 o + c o s 2 3 o + . . . . . . . . + c o s 2 9 0 o k aç t ır ?
44,5
Örnek...7 :
x d a r b i r a ç ı o lm ak ü ze r e , cos(x)=
2
ise
3
sin2 (x)−tan 2 (x) k aç t ı r ?
−25
36
1
tan2 x−
+sin2 x+cos2 x=?
cos 2 x
0
Örnek...9 :
T B Z b i r d ik ü ç g e n
^
m (TMZ )=90 o
^
m (BTZ)=90 o
|TM|=6 br
|MZ|=4 br i s e
^
cos( TBM) k a ç t ı r ?
www.matbaz.com
Örnek...8 :
y
Standart
p o zi s yo n d a
S(0,c)
( köşesi
orijin ve
B
başlangıç
kenarı Ox
P
L
ek s e n i )
v e r i lm i ş v e
R(s,0)
ölçüsü θ
K A
x
olan
a ç ın ın
b i r im
ç em b e r
ü ze r i n d e
gördüğü
ya yı n b i t im n o k t a s ı P ( x , y) n o k t a s ı o l s u n .
P ( x , y) n ok t a s ı n d a b i r i m ç e m b e r e ç i zi l e n
t e ğ e t i n x e k s e n i n i k e s t i ğ i R n ok t a s ın ın
a p s i s i n e θ n ın s ek a n t ı ; y e k s e n i n i
k e s t i ğ i S n ok t a s ın ı n o r d i n a t ın a θ n ın
k o s ek a n t ı d e n i r. θ r e e l s a yıs ı n ı s e c θ
i l e e ş l e ye n f on k s i yo n a s ek a n t f o n k s i yo n u ;
c o s e c θ i l e e ş l e ye n f o nk s i yo n a i s e
k o s ek a n t f on k s i yo n u d e n i r.
SONUÇLAR
cosec(θ)=
sec(θ)=
1
cos θ
Örnek...11 :
Ta b l o d a b o ş k a l a n ye r l e r i d o l d u r u n u z.
T
1. Bölge
2. Bölge
3. Bölge
4. Bölge
cos
6
B
1
sinθ
sin
M
4
Z
3 √ 13
13
+
tan
−
cot
sec
Örnek...12 :
a=cos190o , b=sin170o , c=tan70o , d=sec320o
e = c o s e c 1 7 9 o s a yı l a r ı n ın i ş a r e t l e r i n i
b e l i r l e yi n i z.
−++++
Örnek...10 :
a= c o s 7 0 o
b= s i n 7 0 o
s ı r a l a yı n ı z .
c= t a n 7 0 o s a yı l a r ın ı
a<b<c
11.
11. Sınıf Matematik Konu Anlatımı
Örnek...13 :
√ 2 .(tan 30o . cos 45o +cosec 60 o . sin 45o )=?
√3
3/6
TRİGONOMETRİ − 2
TRİGONOMETRİK FONKSİYONLAR
ş ek l i n d e d e ğ i ş t i r i l i r.
İNDİRGEME BAĞINTILARI
Şekli
y
i n c e l e yi n i z.
Birim
P'(-a,b)
P(a,b)
çemberde
standart
π−θ
biçimde ve
θ
θ
ölçüsü θ
O
K
r a d ya n o l a n b i r
d a r a ç ı a l a l ım .
Bu açının
g ö r d ü ğ ü ya yı n
bitim
noktasının
k oo r d i n a t ı P ( a , b ) o l s u n .
c o s θ = a , s i n θ = b , t a n θ = b / a o lm ak
ü ze r e , π−θ v e π −θ t ü r ü n d e k i a ç ı l a r ın
2
t r i g o n o m e t r ik o r a n l a r ı ş ö yl e h e s a p l a n ır.
Örnek...14 :
A ş a ğ ıd a k i if a d e l e r i n ö zd e ş l e r i n i b u l u n u z.
1) tan(180+x)
tanx
x
2) cos(90+2x)
−sin2x
3) sin(270−4x)
−cos4x
4) cot(90−7x)
tan7x
5) cos(360−4x)
cos4x
6) tan(270+8x)
π−θ BİÇİMİNDEKİ AÇILAR
−cot8x
www.matbaz.com
π−θ ‘ l ık ya yı n b i t i m n ok t a s ı P ' ( − a , b )
olacağından :
c o s (π−θ) = − a = − c o s θ
s i n (π−θ) = b = s i n θ
t a n (π−θ) = − b / a = − t a n θ
c o t (π−θ) = − a / b = − c o t θ o l u r.
π −θ BİÇİMİNDEKİ AÇILAR
2
π −θ ‘ l ı k ya yı n b i t im
2
noktası P(b,a)
olacağından :
c o s π −θ = b = s i n θ
2
s i n π −θ = a = c o s θ
2
t a n π −θ = c o t θ
2
c o t π −θ = t a n θ o l u r.
2
y
7)
a) cos(−x)
b) sin(−x)
c) tan(−x)
d) cot(−x)
e) cosec(−x)
cosx; −sinx; −tanx; −cotx; −cosecx
8) sin(−5x)
−sin5x
P(b,a)
( )
( )
( )
( )
x
O
9) tan (9x−270)
−cot 9x
K
10) cot(4x−180)
cot4x
GENELLEME (GENEL İNDİRGEME BAĞINTISI)
(
)
3π
∓θ (2 π−θ ) o l a r ak
2
v e r i l e n if a d e l e r d e π s a d e l e ş t i r i l m e s i i ç i n
Ölçüsü
π
( 2 ∓θ)
( π±θ )
11) cos240+sin150
0
Ad ı m 1 A ç ı n ı n b ö l g e s i n d e n ya r a l a n ı l a r a k
i ş a r e t b u l u n u r. ( A ç ı d a im a d a r k ab u l e d i l i r )
Ad ı m 2 π , 2 π i ç i n i s im d e ğ i ş t i r i lm e z,
π , 3 π için isim sin↔cos, tan↔cot
2 2
11.
11. Sınıf Matematik Konu Anlatımı
12) tan135o−cos(−240)=?
−1
2
4/6
TRİGONOMETRİ − 2
TRİGONOMETRİK FONKSİYONLAR
DEĞERLENDİRME
7) tan1o. tan3o. tan5o..........tan89o kaçtır?
1
1) sinx+cosx=0,7 ise sinx.cosx kaçtır?
−51
200
8)
2) sinx=0,8 ise sin4x+cos4x kaçtır?
sin2 x +cos 3 x+cosx . sin2 x
ifadesinin en sade
1−cos x
hali nedir?
−337
625
1+ 2 . c o s x
3) cosx−sinx=m ise cos3x−sin3x m türünden
nedir?
3 m−m
2
3
9)
(
)
sin x
sin x
−
. tanx ifadesinin en sade
1−cos x 1+cos x
hali nedir?
2.sin x
4) tanx+cotx=m ise tan3x+cot3x m türünden
nedir?
3
m −3 m
10)
cos2 x
ifadesinin en sade hali
sin x−cosec 2 x+cot 2 x
2
nedir?
−1
5) a=cos10o ,b=cos20o ,c=sin50o sayılarını
sıralaması nasıldır?
a>b>c
11) sin (
6) a=tan100o ,b=tan120o ,c=tan150o sayılarını
sıralaması nasıldır?
7π
7π
) +cos ( ) =?
4
4
0
a<b<c
11.
11. Sınıf Matematik Konu Anlatımı
5/6
TRİGONOMETRİ − 2
TRİGONOMETRİK FONKSİYONLAR
cos
12)
(
)
( )
3π
−x +sin (x−2 π )
2
cot
5π
4
ifadesinin en sade hali
nedir?
0
16) Ş ek i l d e M T Z
e şk e n a r
ü ç g e n d i r.
|MZ|=4.|MB| , i s e
^
cos (MBT)
k a ç t ır ?
−1
√ 13
13) sinx=a ise sin(π+x)+cos ( 3 π −x)+sin(−π−x)
2
ifadesinin a türünden eşiti nedir?
−a
o
o
17) tan24o =p ise tan 114 o−tan 156o ifadesinin p
tan 564 −tan 225
türünden eşiti nedir?
p+1
p
14) x+y= π ve sin x=0,3 ise cos (4x+5y) kaçtır?
5
−√ 91
10
18) sin21o + sin22o + sin23o +..........+ sin290o kaçtır?
45,5
15) Ş e k i l d e M o r t a
n o k t a , T B Z d ik
ü ç g e n d i r.
|TZ|=3 br ,
|BZ|=5 br i s e
^
cos (BMZ)
k aç t ı r ?
T
3
M
B
Z
5
19) Eş kareler kullanılarak elde
edilen şekilde ki x açısı için
tan x kaçtır?
x
−2
√ 13
−3
2
11.
11. Sınıf Matematik Konu Anlatımı
6/6