KONU 1. L˙INEER OPERATÖRLER Tanım 1.1. X ve Y normlu

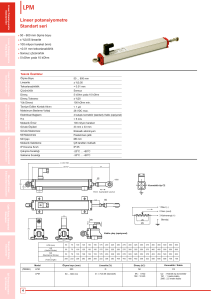
KONU 1. LI·NEER OPERATÖRLER
Tan¬m 1.1. X ve Y normlu uzaylar, A : X ! Y ise tan¬m kümesi D (A)
X olan bir dönüşüm olmak üzere, her ; skalerleri ve her x; y 2 D (A) için
A ( x + y) = Ax + Ay
ise A’ya lineer operatör denir.
Soru 1.1. X = C [a; b] ; Y = R; D (A) = C [a; b] ve her f 2 C [a; b] için
Af =
Zb
f (x) dx
a
bir lineer operatördür.
Soru 1.2. X = Y = C [a; b] ; D (A) = C [a; b] ve her g 2 C [a; b] için
T g (x) = xg (x)
bir lineer operatör müdür? Neden?
Çözüm. Her ; 2 R ve her f; g 2 C [a; b] için
T [ f (x) + g (x)] = x [ f (x) + g (x)] = xf (x)+ xg (x) = T f (x)+ g (x)
elde edilir.
Soru 1.3. X = C 0 [a; b] ; Y = C [a; b] ; D (A) = C 0 [a; b] ve 8f 2 C 0 [a; b] için
0
Af (x) = f (x)
bir lineer operatör oldu¼
gunu gösteriniz.
Çözüm. ; reel say¬lar, f ve g ise C 0 [a; b]’ nin key… elemanlar¬ olmak
üzere
0
0
0
A [ f (x) + g (x)] = [ f (x) + g (x)] = f (x)+ g (x) = Af (x)+ Ag (x)
gerçeklenir.
Al¬şt¬rmalar
1. T : l2 ! l2 olmak üzere (x1 ; x2 :::; ) 2 l2 için
T (x1 ; x2 ; x3 ; :::; ) = (x2 ; x3 ; :::; )
lineer operatör oldu¼
gunu ispatlay¬n¬z.
2. A : L2 (0; ) ! L2 (0; ) ; K (x; t) ise L2 (0; )
man¬olsun. Her f 2 L2 (0; ) için
Af (x) =
Z
K (x; t) f (t) dt
0
1
L2 (0; ) uzay¬n¬n ele-
bir lineer operatör oldu¼
gunu gösteriniz.
3. A : L2 (0; ) ! L2 (0; ) ; D (A) = C 2 [0; ] ve
00
Af (x) = f (x) ; 8f 2 D (A) ile tan¬mlanan A’ n¬n bir lineer operatör
oldu¼
gunu ispatlay¬n¬z.
4. A; B : X ! Y birer lineer operatör ise A + B’de lineer operatör müdür?
Neden?
2