Elektrik Enerjisi Dağıtımı 1 ÇALIŞMA KONULARI • Açma ve Kapama

Elektrik Enerjisi Dağıtımı
1
ÇALIŞMA KONULARI

Açma ve Kapama Elemanlı Sunusundan
1, 3, 4, 24, 25, 26, 27, 28, 36 ve 39. Sayfalar

Dağıtım ve Ölçü Trafoları Sunusundan
3, 4, 9, 15, 18 ve 24. Sayfalar

Gerilim Düşümü Hesapları Üç Fazlı Şebeke
7, 8, 9, 10, 11, 12, 13, 18, 19, 20, 21, 22, 23, 24, 25, 26 ve 27.Sayfalar
Bu Sunuda özellikle 12, 13 ve 27. Sayfalardaki çalışma sorularına bakınız. Soruların cevapları aşağıda
var. Bu soruların benzeri olan iki soru problem olarak sınavda çıkacaktır.
Sınavlarınızda Başarılar dilerim.
Öğr.Gör. Volkan ERDEMİR
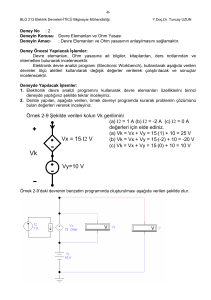
Örnek Çalışma Sorusu1 (12. Sayfa)
𝟖𝒌𝒎 uzunluğundaki bir havai hattının sonunda her biri 𝟏𝟑𝟎𝟎𝒌𝑽𝑨’lik biri 𝒄𝒐𝒔𝝋𝟏 = 𝟎, 𝟔 ve diğeri
𝒄𝒐𝒔𝝋𝟐 = 𝟎, 𝟖 güç katsayısı ile işletilen iki dağıtım transformatörünü beslemektedir. Hat sonundaki gerilim
𝟏𝟎𝒌𝑽’tur.
a) Hatta meydana gelen güç kaybının %𝒑𝒌 = 𝟕, 𝟔 ’dan küçük olması için gerekli anma kesitini,
b) Hat başı gerilimini bulunuz.
l=8km
A
k cu = 56m mm2
x = 0,45 /km
S 1 = 1300kVA
S 2 = 1300kVA
cos = 0,6
cos = 0,8
U 2=10kV
Her bir hattın devre açısı
𝒄𝒐𝒔𝝋𝟏 = 𝟎, 𝟔
𝒄𝒐𝒔𝝋𝟐 = 𝟎, 𝟖
⟹
⟹
a) Her bir trafonun çektiği aktif güçleri
𝝋𝟏 = 𝒄𝒐𝒔−𝟏 𝟎, 𝟔
𝝋𝟐 = 𝒄𝒐𝒔−𝟏 𝟎, 𝟖
⟹
⟹
𝝋𝟏 = 𝟓𝟑, 𝟏𝟑°
𝝋𝟐 = 𝟑𝟔, 𝟖𝟕°
𝑷𝟏 = 𝑺𝟏 . 𝒄𝒐𝒔𝝋𝟏 = 𝟏𝟑𝟎𝟎. 𝒄𝒐𝒔𝟓𝟑, 𝟏𝟑°
𝑷𝟏 = 𝟕𝟖𝟎𝑾
𝑷𝟐 = 𝑺𝟐 . 𝒄𝒐𝒔𝝋𝟐 = 𝟏𝟑𝟎𝟎. 𝒄𝒐𝒔𝟑𝟔, 𝟖𝟕°
𝑷𝟐 = 𝟏𝟎𝟒𝟎𝑾
Üç fazlı sistemlerde görünür formülü 𝑺 = √𝟑. 𝑼. 𝑰 ifadesinden 𝑰 akımı yalnız bırakılarak trafo akımları
aşağıdaki gibi bulunur.
𝑺𝟏
Birinci trafonun çektiği akım
𝑰𝟏 =
√𝟑.𝑼
İkinci trafonun çektiği akım
𝑰𝟐 =
√𝟑.𝑼
𝑺𝟐
=
=
𝟏𝟑𝟎𝟎𝟎𝟎𝟎
√𝟑.𝟏𝟎𝟎𝟎𝟎
𝟏𝟑𝟎𝟎𝟎𝟎𝟎
√𝟑.𝟏𝟎𝟎𝟎𝟎
= 𝟕𝟓, 𝟎𝟓𝟔𝑨
= 𝟕𝟓, 𝟎𝟓𝟔𝑨
Devre endüktif olduğunda, akım geri fazlı olacağından akım fazör olarak gösterilirken açısı (-) işaretli
olarak alınır.
Birinci trafonun çektiği akım fazör olarak
𝑰𝟏 = 𝟕𝟓, 𝟎𝟓𝟔∠ − 𝟓𝟑, 𝟏𝟑°𝑨
𝑰𝟏 = 𝟒𝟓, 𝟎𝟑𝟒 − 𝒋𝟔𝟎, 𝟎𝟒𝟓𝑨
İkinci trafonun çektiği akım fazör olarak
𝑰𝟐 = 𝟕𝟓, 𝟎𝟓𝟔∠ − 𝟑𝟔, 𝟖𝟕°𝑨
𝑰𝟐 = 𝟔𝟎, 𝟎𝟒𝟓 − 𝒋𝟒𝟓, 𝟎𝟑𝟒𝑨
Devreden çekilen toplam akım
𝑰𝑻 = 𝑰𝟏 + 𝑰𝟐 = 𝟒𝟓, 𝟎𝟑𝟒 − 𝒋𝟔𝟎, 𝟎𝟒𝟓 + 𝟔𝟎, 𝟎𝟒𝟓 − 𝒋𝟒𝟓, 𝟎𝟑𝟒
𝑰𝑻 = 𝟏𝟎𝟓, 𝟎𝟕𝟗 − 𝒋𝟏𝟎𝟓, 𝟎𝟕𝟗𝑨
𝑰𝑻 = 𝟏𝟒𝟖, 𝟔𝟎𝟒∠ − 𝟒𝟓°𝑨
Elektrik Enerjisi Dağıtımı
2
𝚤
Hatta meydana gelen aktif güç kaybı 𝒑 = 𝟑. 𝑰𝟐 . 𝑹 ve hattın toplam direnci 𝑹 = 𝒌.𝑺 denklemi
yüzde güç kaybı denkleminde yerine konulursa,
𝒑
𝚤 𝟏
Hattın yüzde güç kaybı
%𝒑𝒌 = 𝟏𝟎𝟎. = 𝟏𝟎𝟎. 𝟑. 𝑰𝟐 . .
𝑷
𝒌.𝑺 𝑷
𝟕, 𝟔 = 𝟏𝟎𝟎. 𝟑. 𝟏𝟒𝟖, 𝟔𝟎𝟒𝟐 .
𝟖𝟎𝟎𝟎
.
𝟏
𝟓𝟔.𝑺 𝟏𝟖𝟐𝟎𝟎𝟎𝟎
𝑺 = 𝟔𝟖, 𝟒𝟐𝟑𝒎𝒎𝟐
Bu kesitte iletken olmadığından standart iletken kesitlerinden 𝑺 = 𝟕𝟎𝒎𝒎𝟐 olarak alınır.
Hat başındaki gerilimin bulunabilmesi için endüktif devre vektör diyagramına göre elde edilen
denklemine göre enine ve boyuna gerilim düşümleri bulunmalıdır.
v'
u')

V1 (U1)
I
V2 (U2)
X.

v (u)
R.
I
v
u)
I
Endüktif devre için Vektör diyagramı
Elektrik devrelerinde faz gerilimi 𝑽 ve hat (fazlar arası)gerilimi 𝑼 ile gösterilir. Yıldız bağlantılı
devrelerde hat gerilimi faz geriliminin √𝟑 katıdır.
Hat gerilimi
𝑼 = √𝟑. 𝑽
𝚤
𝟖𝟎𝟎𝟎
Hattın direnci
𝑹=
Hattın reaktansı
𝑿 = 𝒍. 𝒙 = 𝟖. 𝟎, 𝟒𝟓 = 𝟑, 𝟔𝜴
𝒌.𝑺
=
𝟓𝟔.𝟕𝟎
Fazlar arası boyuna gerilim düşümü
= 𝟐, 𝟎𝟒𝟏𝜴
𝜟𝒖 = √𝟑. 𝜟𝒗 = √𝟑. (𝑹. 𝑰. 𝒄𝒐𝒔𝝋 + 𝑿. 𝑰. 𝒔𝒊𝒏𝝋)
𝜟𝒖 = √𝟑. (𝟐, 𝟎𝟒𝟏. 𝟏𝟒𝟖, 𝟔𝟎𝟒. 𝒄𝒐𝒔𝟒𝟓° + 𝟑, 𝟔. 𝟏𝟒𝟖, 𝟔𝟎𝟒. 𝒔𝒊𝒏𝟒𝟓°)
𝜟𝒖 = 𝟏𝟎𝟐𝟔, 𝟔𝟕𝟑𝑽
Fazlar arası enine gerilim düşümü
𝜹𝒖 = √𝟑. 𝜹𝒗 = √𝟑. (𝑿. 𝑰. 𝒄𝒐𝒔𝝋 − 𝑹. 𝑰. 𝒔𝒊𝒏𝝋)
𝜹𝒖 = √𝟑. (𝟑, 𝟔. 𝟏𝟒𝟖, 𝟔𝟎𝟒. 𝒄𝒐𝒔𝟒𝟓° + 𝟐, 𝟎𝟒𝟏. 𝟏𝟒𝟖, 𝟔𝟎𝟒. 𝒔𝒊𝒏𝟒𝟓°)
𝜹𝒖 = 𝟐𝟖𝟑, 𝟕𝟒𝟏𝑽

V1 (U1)
V2 (U2)
v u)
v
u)
Hat başı geriliminin bulunması için kullanılan vektör diyagramı
Hat başı hat gerilimi
𝑼𝟏 = √𝜹𝒖𝟐 + (𝑼𝟐 + ∆𝒖)𝟐
𝑼𝟏 = √𝟐𝟖𝟑, 𝟕𝟒𝟏𝟐 + (𝟏𝟎𝟎𝟎𝟎 + 𝟏𝟎𝟐𝟔, 𝟔𝟕𝟑)𝟐
𝑼𝟏 = 𝟏𝟏𝟎𝟑𝟎, 𝟑𝟐𝟑𝑽
Elektrik Enerjisi Dağıtımı
3
Örnek Çalışma Sorusu2 (13. Sayfa)
Üç adet Asenkron motor (ASM), bara gerilimi 𝟐𝟑𝟐/𝟒𝟎𝟎𝑽 olan bir güç panosundan bakır iletkenli bir
yeraltı kablosu ile beslenmektedir. Motorların nominal gerilimleri 𝟐𝟐𝟎/𝟑𝟖𝟎𝑽’tur. Hattın en sonundaki
motorun geriliminin 𝟐𝟐𝟎/𝟑𝟖𝟎𝑽 olması için besleme hattının gerilim düşümü en fazla %𝟑 olacak şekilde
kesitini hesaplayınız. Seçilen kesit değerine göre toplam gerilim düşümünü tekrar hesaplayınız.
k cu = 56m mm2
80m
120m
80m
220/380V
232/400V
M
M
P1 = 8kW
cos = 0,83
M
P2 = 15kW
cos = 0,83
%e3
P3
%e2
P2+P3
%e1
P1+P2+P3
P3 = 10kW
cos = 0,83
NOT: Alçak gerilimi şebekesinde enine gerilim düşümü ve 𝒇(𝝋) = 𝟏 ± 𝑿𝑹 𝒕𝒂𝒏𝝋 kısmı ihmal edilir.
%𝜺 =
Yüzde gerilim düşümü olarak
𝟏𝟎𝟎.𝑷.𝒍
𝒌.𝑺.𝑼𝟐
(𝑽) denklemini
kullanarak hatlar arasındaki
gerilimi düşümünü elde edilir. 𝑳𝟏 hattının gücü 𝑷𝟏 + 𝑷𝟐 + 𝑷𝟑 , 𝑳𝟐 hattının gücü 𝑷𝟐 + 𝑷𝟑 , ve 𝑳𝟑 hattının
gücü 𝑷𝟑 alınarak her bir hattın gerilim düşümü hesaplanır. Toplam gerilim düşümü 𝑳𝟏 , 𝑳𝟐 ve 𝑳𝟑 hatlarındaki
gerilim düşümlerinin toplamı kadar olur.
Toplam gerilim düşümü
%𝜺𝑻 = %𝜺𝒍𝟏 + %𝜺𝒍𝟐 + %𝜺𝒍𝟑
%𝜺𝑻 =
𝟏𝟎𝟎.(𝑷𝟏 +𝑷𝟐 +𝑷𝟑 ).𝒍𝟏
𝒌.𝑺.𝑼𝟐
+
𝟏𝟎𝟎.(𝑷𝟐 +𝑷𝟑 ).𝒍𝟐
𝒌.𝑺.𝑼𝟐
+
𝟏𝟎𝟎.𝑷𝟑 .𝒍𝟑
𝒌.𝑺.𝑼𝟐
En fazla %3 lük gerilim düşümüne izin olduğuna göre uygun kesit değeri için aşağıdaki denklem kullanılır.
𝟑=
𝑺=
𝟏𝟎𝟎.(𝟖𝟎𝟎𝟎+𝟏𝟓𝟎𝟎𝟎+𝟏𝟎𝟎𝟎𝟎).𝟏𝟐𝟎
𝟓𝟔.𝑺.𝟑𝟖𝟎𝟐
+
𝟏𝟎𝟎.(𝟏𝟓𝟎𝟎𝟎+𝟏𝟎𝟎𝟎𝟎).𝟖𝟎
𝟓𝟔.𝑺.𝟑𝟖𝟎𝟐
+
𝟏𝟎𝟎.𝟏𝟎𝟎𝟎𝟎.𝟖𝟎
𝟓𝟔.𝑺.𝟑𝟖𝟎𝟐
𝟏𝟎𝟎.[(𝟖𝟎𝟎𝟎+𝟏𝟓𝟎𝟎𝟎+𝟏𝟎𝟎𝟎𝟎).𝟏𝟐𝟎+(𝟏𝟓𝟎𝟎𝟎+𝟏𝟎𝟎𝟎𝟎).𝟖𝟎+𝟏𝟎𝟎𝟎𝟎.𝟖𝟎]
𝟓𝟔.𝟑.𝟑𝟖𝟎𝟐
𝑺 = 𝟐𝟕, 𝟖𝟔𝟔𝒎𝒎
𝟐
Bu kesitte iletken olmadığından standart iletken kesitlerinden 𝑺 = 𝟑𝟓𝒎𝒎𝟐 olarak alınır.
𝑺 = 𝟑𝟓𝒎𝒎𝟐 ‘lik iletken kesitine göre toplam gerilim düşümü
%𝜺𝑻 =
%𝜺𝑻 =
𝟏𝟎𝟎.(𝑷𝟏 +𝑷𝟐 +𝑷𝟑 ).𝒍𝟏
𝒌.𝑺.𝑼𝟐
+
𝟏𝟎𝟎.(𝑷𝟐 +𝑷𝟑 ).𝒍𝟐
𝒌.𝑺.𝑼𝟐
𝟏𝟎𝟎.(𝟖𝟎𝟎𝟎+𝟏𝟓𝟎𝟎𝟎+𝟏𝟎𝟎𝟎𝟎).𝟏𝟐𝟎
%𝜺𝑻 = 𝟐, 𝟑𝟖𝟗
𝟓𝟔.𝟑𝟓.𝟑𝟖𝟎𝟐
+
+
𝟏𝟎𝟎.𝑷𝟑 .𝒍𝟑
𝒌.𝑺.𝑼𝟐
𝟏𝟎𝟎.(𝟏𝟓𝟎𝟎𝟎+𝟏𝟎𝟎𝟎𝟎).𝟖𝟎
𝟓𝟔.𝟑𝟓.𝟑𝟖𝟎𝟐
+
𝟏𝟎𝟎.𝟏𝟎𝟎𝟎𝟎.𝟖𝟎
𝟓𝟔.𝟑𝟓.𝟑𝟖𝟎𝟐
Elektrik Enerjisi Dağıtımı
4
Örnek Çalışma Sorusu3 (27.Sayfa)
Şekildeki gibi verilmiş olan bir alçak gerilim şebekesi iki ucundan beslenmektedir. Nominal gerilimi
𝟏𝟓𝒌𝑽, hat kesiti 𝑺 = 𝟏𝟐𝟎𝒎𝒎𝟐 ve 𝒌 = 𝟑𝟓𝒎/𝒐𝒉𝒎. 𝒎𝒎𝟐 ve 𝒙 = 𝟎, 𝟒𝒐𝒉𝒎/𝒌𝒎 ‘dir.
Her bir hat parçasındaki akımları hesaplayarak fazör diyagramı üzerinde gösteriniz.
88kW
cos=0,8
60,8kVAR
cos=0,8
A
I
l2=810
m
50m
=10
B
l1
1
l 3=
U=15kV
II
l4=527m
10
5m
C
113kVA
cos=0,8
A hattının devre açısı
B hattının devre açısı
C hattının devre açısı
𝒄𝒐𝒔𝝋𝑨 = 𝟎, 𝟖
𝒄𝒐𝒔𝝋𝑩 = 𝟎, 𝟖
𝒄𝒐𝒔𝝋𝑪 = 𝟎, 𝟖
𝝋𝟏 = 𝒄𝒐𝒔−𝟏 𝟎, 𝟖
⟹
⟹
⟹
𝝋𝟏 = 𝟑𝟔, 𝟖𝟕°
−𝟏
⟹
𝝋𝟐 = 𝟑𝟔, 𝟖𝟕°
−𝟏
⟹
𝝋𝟐 = 𝟑𝟔, 𝟖𝟕°
𝝋𝟐 = 𝒄𝒐𝒔 𝟎, 𝟖
⟹
𝝋𝟐 = 𝒄𝒐𝒔 𝟎, 𝟖
İlk önce her bir hattan çekilen akımların fazör gösterimleri bulunur.
A hattından çekilen akım
𝑰𝑨 =
𝑷𝑨
√𝟑.𝑼.𝒄𝒐𝒔𝝋𝑨
=
𝟖𝟖𝟎𝟎𝟎
√𝟑.𝟏𝟓𝟎𝟎𝟎.𝟎,𝟖
= 𝟒, 𝟐𝟑𝟒𝑨
𝑰𝑨 = 𝟒, 𝟐𝟑𝟒∠ − 𝟑𝟔, 𝟖𝟕°𝑨 (Geri fazlı olduğundan açının işareti eksi)
𝑰𝑨 = 𝟑, 𝟑𝟖𝟕 − 𝒋𝟐, 𝟓𝟒𝟎𝑨
A hattından çekilen akımın aktif ve reaktif bileşenleri
B hattından çekilen akım
𝑸𝑩
𝑰𝑩 =
√𝟑.𝑼.𝒔𝒊𝒏𝝋𝑩
=
𝑰𝑨𝒂 = 𝟑, 𝟑𝟖𝟕𝑨
𝟔𝟎𝟖𝟎𝟎
√𝟑.𝟏𝟓𝟎𝟎𝟎.𝒔𝒊𝒏𝟑𝟔,𝟖𝟕°
𝑰𝑨𝒒 = 𝟐, 𝟓𝟒𝟎𝑨
= 𝟑, 𝟗𝑨
𝑰𝑩 = 𝟑, 𝟗∠ − 𝟑𝟔, 𝟖𝟕°𝑨 (Geri fazlı olduğundan açının işareti eksi)
𝑰𝑩 = 𝟑, 𝟏𝟐 − 𝒋𝟐, 𝟑𝟒𝑨
B hattından çekilen akımın aktif ve reaktif bileşenleri
C hattından çekilen akım
𝑰𝑪 =
𝑺𝑪
√𝟑.𝑼
=
𝟏𝟏𝟑𝟎𝟎𝟎
√𝟑.𝟏𝟓𝟎𝟎𝟎
𝑰𝑩𝒂 = 𝟑, 𝟏𝟐𝑨
𝑰𝑩𝒒 = 𝟐, 𝟑𝟒𝑨
= 𝟒, 𝟑𝟒𝟗𝑨
𝑰𝑪 = 𝟒, 𝟑𝟒𝟗∠ − 𝟑𝟔, 𝟖𝟕°𝑨 (Geri fazlı olduğundan açının işareti eksi)
𝑰𝑪 = 𝟑, 𝟒𝟕𝟗 − 𝒋𝟐, 𝟔𝟎𝟗𝑨
C hattından çekilen akımın aktif ve reaktif bileşenleri
𝑰𝑪𝒂 = 𝟑, 𝟒𝟕𝟗𝑨
𝑰𝑪𝒒 = 𝟐, 𝟔𝟎𝟗𝑨
Toplam bileşke aktif akım
𝑰𝒂𝑻 = 𝑰𝑨𝒂 + 𝑰𝑩𝒂 + 𝑰𝑪𝒂 = 𝟑, 𝟑𝟖𝟕 + 𝟑, 𝟏𝟐 + 𝟑, 𝟒𝟕𝟗 = 𝟗, 𝟗𝟖𝟔𝑨
Toplam bileşke reaktif akım
𝑰𝒒𝑻 = 𝑰𝑨𝒒 + 𝑰𝑩𝒒 + 𝑰𝑪𝒒 = 𝟐, 𝟓𝟒 + 𝟐, 𝟑𝟒 + 𝟐, 𝟔𝟎𝟗 = 𝟕, 𝟒𝟖𝟗𝑨
88kW
cos=0,8
60,8kVAR
cos=0,8
A
I
l 1=
l2=810
0m
105
B
l 3=
U=15kV
II
m
l4=527m
11
0
C
113kVA
cos=0,8
5m
Her bir dağıtım noktasının I nolu hatta uzaklığı
alınırsa, II nolu hattan gelen aktif( 𝑰𝒂𝟐 ) ve reaktif (𝑰𝒒𝟐 )
akımlar bulunur. Bunun için A, B ve C noktalarının I nolu hatta
olan uzaklıkları akım ile çarpılarak toplanır ve toplam
uzunluğa bölünür.
Elektrik Enerjisi Dağıtımı
5
II nolu hattan gelen aktif akım
𝑰𝒂𝟐 =
𝑰𝑨𝒂 .𝑳𝟏 +𝑰𝑩𝒂 (𝑳𝟏 +𝑳𝟐 )+𝑰𝑪𝒂 (𝑳𝟏 +𝑳𝟐 +𝑳𝟑 )
𝟑,𝟑𝟖𝟕.𝟏𝟎𝟓𝟎+𝟑,𝟏𝟐.(𝟏𝟎𝟓𝟎+𝟖𝟏𝟎)+𝟑,𝟒𝟕𝟗.(𝟏𝟎𝟓𝟎+𝟖𝟏𝟎+𝟏𝟏𝟎𝟓)
=
𝑳𝟏 +𝑳𝟐 +𝑳𝟑 +𝑳𝟒
𝟏𝟎𝟓𝟎+𝟖𝟏𝟎+𝟏𝟏𝟎𝟓+𝟓𝟐𝟕
= 𝟓, 𝟔𝟑𝟒𝑨
I nolu hattın aktif akımı
𝑰𝒂𝟏 = 𝑰𝒂𝑻 − 𝑰𝒂𝟐 = 𝟗, 𝟗𝟖𝟔 − 𝟓, 𝟔𝟑𝟒 = 𝟒, 𝟑𝟓𝟐𝑨
II nolu hattan gelen reaktif akım
𝑰𝒒𝟐 =
𝑰𝑨𝒒 .𝑳𝟏 +𝑰𝑩𝒒 (𝑳𝟏 +𝑳𝟐 )+𝑰𝑪𝒒 (𝑳𝟏 +𝑳𝟐 +𝑳𝟑 )
𝑳𝟏 +𝑳𝟐 +𝑳𝟑 +𝑳𝟒
𝟐,𝟓𝟒.𝟏𝟎𝟓𝟎+𝟐,𝟑𝟒.(𝟏𝟎𝟓𝟎+𝟖𝟏𝟎)+𝟐,𝟔𝟎𝟗.(𝟏𝟎𝟓𝟎+𝟖𝟏𝟎+𝟏𝟏𝟎𝟓)
=
𝟏𝟎𝟓𝟎+𝟖𝟏𝟎+𝟏𝟏𝟎𝟓+𝟓𝟐𝟕
= 𝟒, 𝟐𝟐𝟓𝑨
I nolu hattın reaktif akımı
𝑰𝒒𝟏 = 𝑰𝒒𝑻 − 𝑰𝒒𝟐 = 𝟕, 𝟒𝟖𝟗 − 𝟓, 𝟗𝟑𝟏 = 𝟏, 𝟓𝟓𝟖𝑨
88kW
cos=0,8
Çözümün ikinci yolu
Her bir dağıtım noktasının II nolu hatta uzaklığı
alınırsa, I nolu hattan gelen aktif ( 𝑰𝒂𝟏 ) ve reaktif (𝑰𝒒𝟏 )
akımlar bulunur. Bunun için A, B ve C noktalarının II nolu
hatta olan uzaklıkları akım ile çarpılarak toplanır ve toplam
uzunluğa bölünür.
60,8kVAR
cos=0,8
A
l1
I
= 10
l2=810
B
m
l 3=
U=15kV
l4=527m
II
11
05
C
113kVA
cos=0,8
I nolu hattan gelen toplam aktif akım
𝑰𝒂𝟏 =
m
50m
𝑰𝑨𝒂 .(𝑳𝟐 +𝑳𝟑 +𝑳𝟒 )+𝑰𝑩𝒂 .(𝑳𝟑 +𝑳𝟒 )+𝑰𝑪𝒂 .𝑳𝟒
𝑳𝟏 +𝑳𝟐 +𝑳𝟑 +𝑳𝟒
=
𝟑,𝟑𝟖𝟕.(𝟖𝟏𝟎+𝟏𝟏𝟎𝟓+𝟓𝟐𝟕)+𝟑,𝟏𝟐.(𝟏𝟏𝟎𝟓+𝟓𝟐𝟕)+𝟑,𝟒𝟕𝟗.𝟓𝟐𝟕
𝟏𝟎𝟓𝟎+𝟖𝟏𝟎+𝟏𝟏𝟎𝟓+𝟓𝟐𝟕
= 𝟒, 𝟑𝟓𝟏𝑨
II nolu hattın toplam aktif akımı
𝑰𝒂𝟐 = 𝑰𝒂𝑻 − 𝑰𝒂𝟏 = 𝟗, 𝟗𝟖𝟔 − 𝟒, 𝟑𝟓𝟏 = 𝟓, 𝟔𝟑𝟓𝑨
I nolu hattan gelen toplam reaktif akım
𝑰𝒒𝟏 =
𝑰𝑨𝒒 .(𝑳𝟐 +𝑳𝟑 +𝑳𝟒 )+𝑰𝑩𝒒 .(𝑳𝟑 +𝑳𝟒 )+𝑰𝑪𝒒 .𝑳𝟒
𝑳𝟏 +𝑳𝟐 +𝑳𝟑 +𝑳𝟒
=
𝟐,𝟓𝟒.(𝟖𝟏𝟎+𝟏𝟏𝟎𝟓+𝟓𝟐𝟕)+𝟐,𝟑𝟒.(𝟏𝟏𝟎𝟓+𝟓𝟐𝟕)+𝟐,𝟔𝟎𝟗.𝟓𝟐𝟕
𝟏𝟎𝟓𝟎+𝟖𝟏𝟎+𝟏𝟏𝟎𝟓+𝟓𝟐𝟕
= 𝟑, 𝟐𝟔𝟒𝑨
II nolu hattın toplam reaktif akımı
𝑰𝒒𝟐 = 𝑰𝒒𝑻 − 𝑰𝒒𝟏 = 𝟕, 𝟒𝟖𝟗 − 𝟑, 𝟐𝟔𝟒 = 𝟒, 𝟐𝟐𝟓𝑨
Bulunan değerlere göre fazör diyagramı çizilirse akımların çakışma noktasının B noktası olduğu görülürür.
I a1=4,352A
I q1=3,264A
B
A
I
I ABa=4,352-1,732=2,523A
I ABq=3,264-2,54=0,724A
C
I BCa=5,634-3,479=2,155A
I BCq=4,225-2,609=1,606A
I Aa=3,387A
I Ba=3,12A
I Ca=3,479A
I Aq=2,54A
I Bq=2,34A
I Cq=2,609A
II
I a2=5,634A
I q2=4,225A