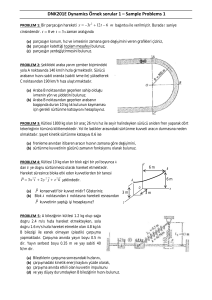
DİNAMİK DERS NOTLARI
Kaynaklar:
Engineering Mechanics: Dynamics, SI Version, 6th Edition, J. L.
Meriam, L. G. Kraige
Vector Mechanics for Engineers: Dynamics, Sixth Edition, Beer and
Johnston
Doç.Dr. Cesim ATAŞ
1. MADDESEL NOKTANIN (PARÇACIK) KİNEMATİĞİ
(KINEMATICS OF PARTICLES)
1.1 Doğrusal Hareket (rectilinear motion)
P
O
Bir parçacığın düz bir çizgi
x
boyunca hareketi doğrusal
x
hareket olarak adlandırılır.
+
Parçacığın hızı;
dx
v=
dt
ivme a hızın (v) zamana (t) göre türevi ile bulunur;
dv
a=
dt
veya
d 2x
a= 2
dt
İvme (a) zamandan bağımsız olarak da
ifade edilebilir:
dv
a=v
dx
Hız (v) ve ivme (a) vektörel büyüklüklerdir. Burada; doğrultusu
belli olan bir çizgi boyunca hareket söz konusudur. İşlemler de hız
için bulunan pozitif ve negatif değerler hareket yönünü temsil
ederken, pozitif ivme değerleri hızlanmaya negatif değerler ise
parçacığın yavaşlamasına işaret eder.
• Düzgün Doğrusal Hareket:
x = xo + vt
v= sabit
a= 0
• Düzgün Değişen Doğrusal Hareket:
v = vo + at
x = xo + vot +
1
2
at2
v2 = vo2 + 2a(x - xo )
(a= sabit)
•Bağıl Hareket:
xB/A B’nin A’ya göre bağıl konumu (aslında konum vektörü) olmak
üzere;
O
A
xA
B
xB/A
xB
xB = xA + xB/A
;
vB = vA + vB/A
;
aB = aA + aB/A
x
Problem çözümlerinde grafik yöntemler de kullanılabilir.Grafik
çözümler genellikle x - t, v - t , ve a - t eğrileri kullanılarak yapılır.
a
Herhangi bir t anında,
v
t1
v = (x – t) eğrisinin eğimi
t
t2
t2
v2
v1
v2 - v1 = ∫ a dt
t1
t1
t2
Ortalama hız ; v =
Δx
Δt
a = (v - t) eğrisinin eğimi
Ortalama ivme ; a = Δv
t
Δt
x
t2
x2
x1
x2 - x1 = ∫ v dt
t1
t1
t2
t
Herhangi bir zaman aralığında
t1- t2,
v2 - v1 = (a – t) eğrisinin altında kalan alan
x2 - x1 = (v - t ) eğrisinin altında kalan alan
1.2 Eğrisel Hareket (curvilinear motion)
y
v
r: göz önüne alınan parçacığın
herhangi bir andaki “konum vektörü”
r
P
Parçacığın hızı;
s
Po
dr
v=
dt
x
O
Hız vektörü daima parçacığın hareket yörüngesine teğettir ve
şiddeti (v), parçacığın aldığı yolun (s)zamana göre türevi ile bulunur.
a
y
r
O
ds
v=
dt
Fakat, genellikle, ivme hareket yörüngesine teğet
değildir. Hız vektörlerinin yörüngesine teğettir.
P
Po
s
x
dv
a=
dt
1.3 Hız ve İvmenin Dik Bileşenleri
y
y
ay
vy
P
vx
vz
j
k
z
r=xi+yj+zk
dr
v=
dt
.
vx = x
..
ax = x
P
az
r yj
xi
i
zk
j
x
k
z
dv
a=
dt
.
.
vy = y
vz = z
..
..
ay = y
az = z
ax
r
i
x
Örnek; Bir mermin 2-Boyutlu hareketi
1.4 Öteleme Yapan Bir Eksen Takımına Göre Bağıl Hareket
x-y-z; sabit eksen takımı
x’-y’-z’; hareketli eksen takımı
vB/A: B’nin A’ya göre bağıl hızı;
aB/A : B’nin A’ya göre bağıl ivmesi
rB = rA + rB/A
vB = vA + vB/A
aB = aA + aB/A
1.5 Normal ve Teğetsel Koordinatlar (n-t)
y
Bazen, hız ve ivme bileşenlerini kartezyen koordinatlardan
(x, y, ve z ) daha farklı bir sistemde tanımlamak daha
kolaydır. Örneğin eğrisel bir yörüngede hareket eden bir P
parçacığını yörüngeye teğet ve yörüngeye normal bileşenler
şeklinde ifade edebiliriz. Bu durumda;
v = vet
;
v2
dv
a=
et +
en
ρ
dt
C
v2
an =
e
ρ n
P
O
dv
at = dt et
x
1.6 Kutupsal (Polar) Koordinatlar (r
ve θ)
eθ
Düzlemdeki eğrisel bir yörüngede hareket eden
bir parçacığın konumunu r ve θ ile ifade etmek
mümkün ise hız ve ivmeyi de radyal ve ona dik
doğrultudaki bileşenlerine ayırmak mümkün
olmaktadır. er ve eθ birim vektörlerdir. Hız ve ivme
bileşenleri;
.
.
v = rer + rθeθ
..
.. . 2
..
a = (r - rθ )er + (rθ + 2rθ)eθ
r = r er
er
P
θ
O
Burada noktalar zamana göre türevi temsil etmektedir. Bu durumda skaler
bileşenler şu şekilde ifade edilebilir:
.
vr = r
.. . 2
ar = r - rθ
.
vθ = rθ
..
..
aθ = rθ + 2rθ
x
2. MADDESEL NOKTANIN (PARÇACIK) KİNETİĞİ:
NEWTON’UN İKİNCİ KANUNU
(KINETICS OF PARTICLES:NEWTON’S SECOND LAW)
2.1 Giriş
m:kütle,
Σ F: bileşke kuvvet vektörü
a: ivme vektörü
Newton’un ikinci kanunu
Σ F = ma
Bir parçacığın lineer momentumu, “L = mv” ile ifade edildiğinde
Newton’un ikinci kanunu aşağıdaki gibi yazılabilir.
.
ΣF=L
Bu bağıntı; bir parçacığa etkiyen bileşke kuvvetin, parçacığın lineer
momentumu’nun değişim hızına eşit olduğu anlamına gelir.
ay
y
P
az
Bir parçacığın hareketiyle ilgili bir problemi çözerken;
Σ F = ma yerine skaler bileşenleri içeren bağıntılar da
kullanılabilir.
ax
Kartezyen koordinatlarda;
x
z
Σ Fz = maz
Teğetsel ve Normal koordinatlarda,
y
an
at
P
x
O
r
dv
Σ Ft = mat = m
dt
v2
Σ Fn = man = m
ρ
Kutupsal koordinatlarda ,
aθ
O
Σ Fx = max Σ Fy = may
θ
P
ar
x
.. . 2
Σ Fr = mar= m(r - rθ )
..
..
Σ Fθ = maθ = m(rθ + 2rθ)
2.2 Açısal Momentum
HO
y
mv
φ
O
z
r
P
x
Bir parçacığın O noktasına göre
açısal momentumu (angular
momentum) (HO); parçacığın lineer
momentumu’nun (mv) O noktasına
göre momenti olarak tanımlanabilir.
HO = r x mv
Burada HO ; “r” and “mv” vektörlerini içeren düzleme dik bir
vektördür. Şiddeti;
HO = rmv sin φ
i
j
k
HO = x
y
z
mvx mvy mvz
y
mv
HO
O
z
φ
r
P
x
i
j
k
HO = x
y
z
mvx mvy mvz
xy düzleminde hareket eden bir parçacık için; z = vz = 0. Açısal momentum xy
düzlemine her zaman diktir. Bu durumda açısal momentum sadece şiddeti ile
de tanımlanabilir:
HO = Hz = m(xvy - yvx)
.
Açısal momentum (HO) daki değişim hızını HO hesaplayıp
Newton’un ikinci kanununu uygularsak;
.
Σ M O = HO
Bu bağıntıya göre; bir parçacığa etki eden kuvvetlerin O noktası
etrafındaki bileşke momentlerinin, parçacığın O etrafındaki açısal
momentumundaki değişim oranına/hızına eşittir.
3. MADDESEL NOKTANIN (PARÇACIK) KİNETİĞİ:
ENERJİ VE MOMENTUM METOTLARI
(KINETICS OF PARTICLES: ENERGY AND MOMENTUM METHODS )
Kinetik analizde ivme kullanılmadan analiz yapma imkanı veren iki
yöntem vardır: “iş-enerji” ve “impuls-momentum”. Her iki yönteme ait
bağıntılar Newton’un 2. kanunundan yararlanılarak elde edilebilir.
s2
A2
ds
A
dr
α
A1
s1
•Bir kuvvetin işi:
Parçacığa etki eden F kuvvetinin küçük
dr deplasmanına karşılık gelen işi;
F
dU = F dr = F ds cos α
s
Böylece, A1 den A2 ye yapılan iş;
U1
2
=
∫
A2
A1
∫
A2
F dr = (Fxdx + Fydy + Fzdz)
A1
•Doğrusal harekette sabit bir kuvvetin işi:
F
A2
α
U1
Δx
A1
•Ağırlığın işi:
W
dy
A1
y2
y1
y
(F cos a) Δx
Ağırlığı W olan bir cismin işi (y1
den y2 ye çıkarıldığında);
Fx = Fz = 0 and
Fy = - W .
y2
A2
A
2=
U1
2=
-
∫
y1
Wdy = Wy1 - Wy2
•Yay kuvvetinin işi:
Bir yayın uyguladığı F kuvvetinin yaptığı
iş (A1’ den A2’ye)
spring undeformed
B
B
AO
dU = -Fdx = -kx dx
U1
A1
x1
B
k x dx =
1
2
2
kx1
-
2
1
kx
2 2
Yayı şekil değiştirmemiş
konumuna dönmeye zorlayan
yay kuvvetlerinin işi pozitif (+) tir.
A
x2
∫
-
x1
F
x
2=
x2
A2
.
•iş-enerji prensibi
T=
Bir parçacığın kinetik enerjisi;
1
2
mv2
Newton’un 2. kanunu kullanılarak iş-enerji prensibi
çıkarılabilir:
T1 + U1
2=
T2
Eğer bir F kuvvetinin yaptığı iş parçacığın takip ettiği yoldan bağımsız ise;
F kuvvetine konservatif kuvvet denir. Yay kuvveti ve ağırlık konservatif
kuvvetlerdir. Bu durumda enerjinin korunumundan söz edilebilir.
T1 + V 1 = T2 + V 2
Buna göre; sadece konservatif kuvvetler etkisinde hareket eden bir
parçacığın, potansiyel enerjisinin ve kinetik enerjisinin toplamı hareket
boyunca sabit kalır.
•İmpuls-momentum prensibi
Bir parçacığın lineer momentumu; parçacık kütlesi ( m) ile hızının (v)
çarpımına eşittir. Newton’un ikinci kanunundan, F = ma, impuls-momentum
bağıntısı şu şekilde çıkarılabilir:
mv1 +
∫
t2
t1
F dt = mv2
mv1 + Imp1
2=
mv2
Eğer parçacık birden fazla kuvvetin etkisinde ise;
mv1 + ΣImp1
2=
mv2
Burada yer alan vektörel büyüklükler bileşenlerine ayrılarak (ör;
x ve y ), impuls-momentum bağıntısı skaler bağıntılar şeklinde
de ifade edilebilir.
Eğer çok büyük impulsif kuvvetler çok küçük bir zaman
aralığında (Δt) etki ediyorsa; impulsif olmayan kuvvetlerin
impulsları ihmal edilebilir:
mv1 + ΣFΔt = mv2
Birden fazla parçacığın impulsif hareketinde;
Σmv1 + ΣFΔt = Σmv2
Burada ikinci terim sadece impulsif dış kuvvetleri içermektedir.
Eğer dış kuvvetlerin impulslarının toplamı “0” ise, parçacıkların
toplam momentumları korunur;
Σmv1 = Σmv2
•Çarpışma:
•Doğru Merkezsel Çarpışma
Çarpışma
doğrultusu
vB
B
A Çarpışma
v’B
B
A
v’A Çarpışma
sonrası
mAvA + mBvB = mAv’A + mBv’B …..(I)
İkinci denklem,çarpışma öncesi ve sonrası hız
ilişkisini ifade eder (çarpışma katsayısını içerir) ;
öncesi
vA
A and B parçacıklarının doğru merkezsel
çarpışma’dan sonraki hızlarını bulmak için iki
denklem kullanılabilir:
Birinci denklem, iki cismin toplam
momentumlarının korunumu;
v’B - v’A = e (vA - vB )….. …..(II)
Çarpışan malzemelerin özelliklerine bağlı olarak,
çarpışma katsayısı (e), 0 ile 1 arasında değerler alır.
e = 0, tam plastik çarpışma.
e = 1 , tam elastik çarpışma.
•Eğik Merkezsel Çarpışma
Line of
Impact
n
t
vB
B
A
vA
t doğrultusunda;
Before Impact
v’B
n
t
v’A
Eğik merkezsel çarpışmada, çarpışan cisimlerin
hızları; çarpışma doğrultusundaki (n) ve temas
yüzeyine teğet doğrultudaki (t) bileşenlerine ayrılır.
Bu durumda bilinmeyenleri bulmak şu 4 bağıntıdan
yararlanılır:
B
vB
A
vA After Impact
(vA)t = (v’A)t
(vB)t = (v’B)t
n doğrultusunda;
mA (vA)n + mB (vB)n = mA (v’A)n + mB (v’B)n
(v’B)n - (v’A)n = e [(vA)n - (vB)n]
Bu bağıntılar, çarpışma öncesi ve sonrası serbest
hareket eden cisimler için çıkarılmış olmakla beraber,
hareketleri sınırlanmış cisimlerin çarpışmasında da
kullanılabilir.
4. RİJİT CİSİMLERİN KİNEMATİĞİ
(KINEMATICS OF RIGID BODIES)
Rijit cisimlerin düzlemdeki hareketi genel olarak 3’e ayrılır: “Ötelenme”,
“Sabit bir eksen etrafında dönme” ve “Genel düzlemsel hareket”.
•Ötelenme
Ötelenmede cisim
üzerindeki tüm noktalar
aynı hız ve aynı ivme ile
hareket ederler.
•Sabit bir eksen etrafında
dönme
•Genel düzlemsel hareket
•Sabit bir eksen etrafında dönme:
z
A’
Z ekseni etrafında dönen P noktasını göz
önüne alırsak; θ’nın gördüğü açı
Δs ise; Δs = BP ⋅ Δθ = r ⋅ sin Φ ⋅ Δθ
B
θ
φ
O
x
A
Δs
Δθ
ds
= lim r ⋅ sin Φ
=
= r θ& sin Φ
v
;
Δt → 0 Δ t
Δt → 0
dt
Δt
P
v = lim
r
θ& = w = açısal hız
y
Yani P’nin hızının şiddeti;
.
ds
v=
= rθ sin φ
dt
dr
P noktasının hız, vektörel çarpımla;
v=
=ωxr
dt
.
şeklinde ifade edilir ve; ω = ωk = θk
Burada ω sabit eksen etrafındaki açısal hıza karşılık gelmektedir.
..
.
dω
α=
= αk = ωk = θk
dt
= açısal ivme
P’nin sabit eksen etrafındaki ivmesi;
a
dv d(ω × r ) dω
dr
=
×r + ω×
=
=
dt
dt
dt
dt
= α × r + ω × v = α × r + ω × ( ω × r)
a = α x r + ω x (ω x r)
y
O
v = ωk x r Düzlemde O noktasından geçen eksen
etrafında dönme; v = ωk x r
P
r
ω = ωk
x
İvme;
a = α x r + ω x (ω x r)
y
O
α = αk
at = αk x r
P
an= -ω2 r
ω = ωk x
r=rxi +ryj yazılırsa
a = α x r – ω2 r= at+ an
at = αk x r
at = rα
an= -ω2 r
an = rω2
İki özel durum:
• Düzgün Dönme (α=0):
dω =sbt
α=
dt
dθ
ω=
dt
θ= θ0+ ωt
• Düzgün Değişen Dönme (α=sbt):
ω= ω0+ αt
1 αt2
θ= θ0+ ω0t +
2
ω2= ω20+ 2α (θ−θ0)
•Genel düzlemsel hareket: hız analizi
vA
vA
y’
vB
A
A
vA
(fixed)
A
ωk
x’
rB/A
vB/A
B
B
Düzlem hareket
=
A ya göre öteleme
B
+ A ya göre dönme
vB/A
vB = vA + vB/A = vA + ωk x rB/A
vB/A = ωk x rB/A ;
vB/A = (rB/A )ω = rω
aB = aA + α x r + ω x (ω x r)
vA
vB
•Ani Dönme Merkezi (ADM):
C
vB
B
A
vA
Bir plakanın düzlemsel
hareketinde, hızla ilgili çözüm
yaklaşımlarından birisi de ani
dönme merkezi (ADM)’ni
kullanmaktır. Ancak C
noktasının ivmesi her zaman
“0” olmayabilir. Bu nedenle
İvme analizinde ADM
yaklaşımı kullanılmaz.
C
vB
vA
•Genel düzlemsel hareket: ivme analizi y’
aA
ωk
aA
aB
B
Düzlem hareket =
aB/A
A
A
A
αk
B
aA
(aB/A)n
(aB/A)t
B
A ya göre öteleme + A ya göre dönme
(aB/A)n
aB = aA + aB/A
aB = aA + α x r + ω x (ω x r)
aB = aA + α x r – ω2 r
aB
x’
aB/A
(aB/A)t
aA
Vektör diyagramı
•Dönen bir eksene göre bağıl hareket
Y
y
B
Bir P parçacığının, sabit bir eksen etrafında ω açısal
hızı ile dönen x-y eksen takımına göre hareketi
(düzlemde) incelenirse; P’nin mutlak hızı:
P
vB = vA + vB/A
r
A
ω
α
x
vP = vB + vP/B= vA + vB/A + vP/B
vP = vA + ω x rB/A+ vbağ
P’nin mutlak ivmesi:
X
aB = aA + aB/A =aA + α x rB/A + ω x (ω x rB/A)
aP = aB + aP/B+ acor
= aA + α x rB/A + ω x (ω x rB/A)+2(ω x vbağ)+ acor
Not: Hız ve ivme için yazılan bağıntılar 3-boyutlu problemler için
de kullanılabilir. Bu durumda , bağıntılardaki vektörel büyüklükleri
3-boyutlu olarak yazmak gerekir.
5. RİJİT CİSİMLERİN KİNETİĞİ (RİJİT CİSİMLERİN DÜZLEMSEL HAREKETİ)
(PLANE MOTION OF RIGID BODIES:FORCES AND ACCELERATIONS)
.
• Kuvvet ve İvme
F4
F1
G
F3
HG
ma
G
Rijit cisimlerin kinetiğinde
kullanılan iki temel bağıntı
vardır:
F2
m: cismin kütlesi
a: kütle merkezinin (G ) ivmesi.
.
ΣF = ma
.
ΣMG = HG
HG : cismin G noktasına göre açısal
momentumun türevi.
HG = Iω
I: rijit plakanın/cismin G noktasından
geçen eksene göre kütle atalet momenti.
HG = Iω = Iα
ω: açısal hız
.
.
F1
F4
ma
F2
G
F3
G
Iα
ΣFx = max
ΣFy = may
Referans düzlemine göre
simetrik olan rijit bir
cismin hareketini ifade
eden bağıntılar skaler
olarak da yazılabilir:
ΣMG = Iα
• Enerji ve Momentum Metotları
İş-enerji prensibi:
U1
2
=
∫
s2
s1
T1 + U1
2=
(F cos α) ds
T2
(Bir kuvvetin işi)
θ açısı ile dönen rijit bir
cisme etkiyen bir kuvvet
çiftinin veya momentin işi:
G
ω
v
O
ω
T1 ve T2 : cismin 1 ve 2
konumlarındaki kinetik
enerjisi
U1 2 : cisme etki eden dış
kuvvetlerin işi
Düzlem harekette bir
cismin kinetik enerjisi:
U1
T=
=
2
∫
θ2
M ds
θ1
1
2
2
1
2
mv + Iω2
Sabit bir eksen etrafında dönen rijit bir
cismin kinetik enerjisi:
T=
Göz önüne alınan rijit cisme sadece
konservatif kuvvetler etki ediyorsa;
enerjinin korunumu ilkesi:
T1 + V1 = T2 + V2
1
2
I
ω
2 O
Parçacığın hareketi için çıkarılan İmpuls ve momentum prensibi rijit cismin hareketi
için de kullanılabilir:
Sist. Momentumu1 + Sist. Dış Imp1
y
mv1
y
∫ Fdt
2=
Sist. Mom.2
y
G
G
Iω2
Iω1
O
mv2
x
O
x
O
x
Çarpışmada da benzer bir yaklaşım kullanılabilir, ancak; çarpışan
cisimlerin kütle merkezleri çarpışma doğrultusu üzerinde değilse buna
eksantrik çarpma (eccentric impact ) denir. Bu durumda; çarpışma
boyunca temasta olan A ve B noktalarının hızları göz önüne alınır.
n
n
B
n
A
vB
A
vA
Çarpışma öncesi
n
B
v’B
v’A
Çarpışma sonrası
(v’B)n - (v’A)n = e[(vA)n - (vB)n]