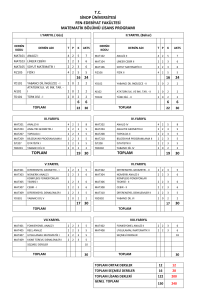
DĠCLE ÜNĠVERSĠTESĠ
FEN-EDEBĠYAT FAKÜLTESĠ
MATEMATĠK BÖLÜMÜ
LÌSANS PROĞRAMI
ZORUNLU-SEÇMELĠ VE DESTEK DERS ĠÇERĠKLERĠ
2005 yılı öncesi GiriĢli öğrenciler için
MAT 101 GENEL MAT. I (Kimya Böl.)
(3 2 4)
MAT 102 GENEL MAT. II (Kimya Böl.)
Temel Kavramlar;
Fonksiyon; Transandant
Fonksiyonlar;
Limitler;
Süreklilik; Türev;
Diferansiyeller; Diferansiyel Hesabın Geometrik
Uygulamaları; Max-Min.; Rolle
Teoremi;
Ortalama Değer Teoremi; Diziler;Seriler
MAT 113 ANALĠZ I
(Fizik Böl.)
Fonksiyonların Seriye Açılımları; Fonksiyonların
DeğiĢiminin Ġncelenmesi Ve Grafiklerinin Çizimi;
Belirsiz Ġntegraller; Belirli Ġntegraller; Belirli
Ġntegralin Geometrik Uygulamaları. Vektörler;
Matrisler; Kısmi Türevler.
(4 2 5)
MAT 114 ANALĠZ II (Fizik Böl.)
Bir Fonksiyonun DeğiĢim Hızı; Koordinatlar;
Artımlar; Bir Doğrunun Denklemi; Fonksiyonlar;
Grafìkler; Fonksiyonların DavranıĢı Ve Türevleri;
Bir Cismin Hızı Ve DeğiĢim Hızları; Limitler;
Limitin Alanları Ve Uygulamaları Ġle Sonsuzluk
Kavramı; Cebirsel Fonksiyonların
Türevleri;
Artan Ve Azalan Fonksiyonlar; Eğri Çizimi;
Rolle Teoremi; Ortalama Değer Teoremi.
FĠZ 111 TEMEL FĠZĠK I
(4 2 5)
Ġntegral Alma; Belirli Ġntegralin Uygulamaları;
Sinüs Ve Cosinüs Türev Ve Ġntegrallerinin
Alınması; Bir Eğri Altındaki Alan; Belirli
Ġntegral Ve Ġntegral Hesabın Temel Teoremleri;
Ġki Eğri Arasındaki Alan; Uzaklık; Hacimler; Bir
Düzlem Eğrisinin Uzunluğu; Dönel Yüzey Alanı;
Momentler Ve Kütle Merkezi; Ağırlık Merkezi;
Pappus Teoremi; ĠĢ; Transandant Fonksiyonlar;
Hiperbolik
Fonksiyonlar; Ġntegral Alma
Yöntemleri.
(2 2 3)
FĠZ 112 TEMEL FĠZĠK II
-Uzunluk, Yoğunluk, Birim Çevirme, Anlamlı
Rakamlar, Koordinat Ve Referans Sistemleri,
Vektörler Ve Skalerler, Ortalama Hız, Ani Hız,
Ġvme, DüĢen Cisimler, Kinematik, Yer DeğiĢtirme,
Eğik AtıĢ, Düzgün Dairesel Hareket, Yüksek
Hızlarda Bağıl Hareket.
-Klasik Mekaniğe GiriĢ, Newton’un Birinci, Ġkinci
Ve Üçüncü Kanunu Ġle Bazı Uygulamaları,
Sürtünme Kuvvetleri
-Sabit Ve DeğiĢen Kuvvetin Yaptığı ĠĢ, Kinetik
Enerji, Güç, Enerji Ve Otomobil, Potansiyel Enerji
MAT 151 SOYUT MATEMATĠK I
(3 2 4)
(2 2 3)
-Elektrik Yüklerinin Özellikleri, Elektrik Alanı,
Yük Dağılımı, Düzgün Bir Elektrik Alandaki Yüklü
Parçacıkların Hareketi, Osiloskop, Gauss Kanunu,
Potansiyel Farkı Ve Elektrik Potansiyeli, Milikan’ın
Yağ Damlası Deneyi, Elektrostatik Uygulamaları,
Kondansatörler, Dielektrikler, Pil, Elektrik Akımı,
Direnç Ve Ohm Kanunu, Ev Aletleri Devrelerinde
Enerji DönüĢümü,
-Seri Ve Paralel Bağlı Dirençler, Kirchoff Kuralları,
Elektrik Cihazları, Wheatstone Köprüsü, Manyetik
Kuvvet, Tork, Manyetik Alandaki Yüklü
Parçacıkların Hareketi, Amper Kanunu, Dünya’nın
Manyetik Alanı.
(4 0 4)
MAT 152 SOYUT MATEMATĠK II
Sembolik Mantık Ve Önermeler, UyuĢma Ve
ÇeliĢme, Bazı Özellikler, Matematik Ġspat
Yolları;
Kümeler Kavramı;
Kümeler Cebiri; Kümeler Ailesi;
Bağıntı; Denklik Bağıntısı;
Sıralama Bağıntıları;
DönüĢümler;
ĠĢlem Kavramı;
Latisler;
Doğal Sayılar, Doğal Sayılarda iĢlemler,
Sayılabilir (sonlu yada sonsuz) kümeler
(4 0 4)
Tam Sayıların KuruluĢu Ve Temel Özellikleri;
Bölme Ve Kalanlı Bölme; Asal Sayılar; Mükemmel
Sayılar Modüler Aritmetik;
Bölünebïlme
Kuralları; Lineer Modüler Aritmetik; Euler
Fonksiyonu; Wilson; Euler Ve Küçük Fermat
Teoremleri; Rasyonel Sayılar; Devreden Ve
Devretmeyen Rasyonel Sayılar; Gerçel Sayılar;
Cauchy Dizileri; Yakınsaklık Ve Sınırlılık;
Ġrrasyonel Sayılar; KarmaĢık Sayılar Ve Cisim
OluĢu; KarmaĢık Sayıların ÇeĢitli Gösterimleri;
Üçgen EĢitsizlikleri; Kutupsal Biçimi; Argüment;
Üstel Form; Logaritması; Bazı Nokta Kümeleri;
Konveks
Küme;
Tıkız
(Kompakt)
Lık;
Bağlantılılık.
MAT 161 DOĞRUSAL CEBĠR I
(3 2 4)
MAT 162 DOĞRUSAL CEBĠR II
(3 2 4)
Vektör Uzayları;Vektörlerin Toplama ĠĢlemleri;
Skaler Ġle Çarpma; DıĢ ĠĢlemler; Bir Cismin
Üzerinde Tanımlanan Standart Vektör Uzayları;
Ġç
Çarpım Uzayları;
Ortogonal
Vektör
Sistemleri;
Lìneer Bağımlılık; Alt Uzayların
Boyutları; Direkt Toplamı; Matrisin EĢitliği; Matris
Toplamı Ve Skaler Ġle Çarpım; Matris Çarpımı;
Birim Matris; Ters Matris; Bir Matrisin
Transpozu.
Permütasyonlar Ve Determinantlar; Denklem
Sistemleri Ve Çözümleri; Matris Polinomları;
Karakteristik Değerler Ve Karakteristik Vektörler;
Polinomlar Ve Polinom Ġdealleri.
MAT 171 ANALĠZ I
MAT 172 ANALĠZ II
(4 2 5)
(42 5)
Reel
Sayılar,
Fonksiyonlar;
Trigonometrik
Fonksiyonlar, Üstel Ve Logaritmik Fonksiyonlar
Limit Ve Süreklilik, Limitin Tanımı Ve Süreklilik
Limit
Teoremleri
Ve
Süreklilik,
Türev,
Türevlenebilir Fonksiyonlar, Zincir Kuralı, Yüksek
Mertebeden Türevler, Kesin Türevler, YaklaĢımlar,
Türevin Uygulamaları, Maksimum Ve Minimum
Değerler, Ġçe Bükeylik Ve Dönüm Noktaları
Belirli Ġntegral Ġçin Ön Bilgi, Ġntegralin Temel
Teoremi, Belirsiz Ġntegral Ve Ġntegral Alma
Kuralları, Ters Fonksiyon, Üstel Fonksiyonlar,
Logaritmik Fonksiyonlar, Hiperbolik Fonksiyonlar,
Ters Trigonometrik Fonksiyonlar, L’Hospital
Kuralı, Ġntegral Alma Teknikleri, Kısmi Ġntegral,
Trigonometrik Ġntegral, Ġntegral Uygulamaları,
Hacim, Kabuk Yöntemi, Diziler Ve Seriler, Sonsuz
Serileri, Yakınsaklık, Kuvvet Serileri
MAT 181 TEMEL MATEMATĠK I
MAT 182 TEMEL MATEMAT
(2 - 2)
Matematiksel Mantık
Õnermeler Ve Ġspat Yöntemleri
Kümeler Ve Cebiri
Cebírsel Ve Geometrik Bazı EĢitsizlikler
Rasyonel Ve Ġrrasyonel Sayılar
Matematiksel Sonsuz
EĢdeğer Ve Parçalanabilen ġekiller
Matematikte Indüksiyon Ve Benzetme
MAT 191 MATEMATĠK SOHBETLER
II
(2 - 2 )
Çok Renk Problemlerinin Tanıtımı
Sayilar Teorisine Ait Bazı Problemler
Geometrik Ġspat Hataları
Yalnız Pergelle Yapılan Çizimler
ÇeĢitli Geometriler
Limit Ve Türev
Diziler, Ġndirgemeli Diziler
(2 - 2)
MAT 192 MATEMATĠK BĠLĠM TARĠHĠ (2- -2)
-Öğrenciyi
Matematikte
KarĢılaĢacakları
Zorlukları AĢma Yönünde Bilinçlendirme Ve
Matematik Yapmaya Isındırma,
-DüĢünürlerin Matematik Hakkındaki GörüĢleri,
-Güncel Matematik TartıĢmaları Hakkında
Bilgilendirme,
-Öğrencinin BakıĢ Açısı,
-Okuma (Ġfade Ve Anlatım),
-AraĢtırma Çabalarının Arttırılması,
-Diğer Bilimsel Faaliyetler.
-Matematik Tarihi Ġle Ġlgili Kaynakça, Ġlkçağ
Matematiği, Ġslam Matematiğinde Yunan Ve Hint
Mirası, Ortaçağ Araplarında Günlük YaĢamda
Matematik, Hint-Arap Sayı Sistemi, Ġslamda Ünlü
Matematikçiler
-Osmanlıda Matematik, Yeniçağ Avrupa'sında
Matematik, Batı’nın Ünlü Matematikçileri,
Matematiğin Fizik, Müzik, Astronomi, Mimarlık
Ve Diğer Bilimlerle ĠliĢkisi
-Matematik Ve Mantık, Zeno Paradoksları,
Matematiğin
Fantastik
Yanları
(Öklid’in
Aksiyomları, Pisagor Ve Ġrrasyonel Sayılar;
Ġlkçağ’ın Çözülemeyen Ünlü Üç Problemi; Sayısının
Öyküsü,
Logaritmanın
Öyküsü,
Fibonacci Ve Ünlü Dizisi, Doğada Ve Güzel
Sanatlarda Altın Oran; Pascal Üçgeni; Gauss’un
Matematiksel YaĢam Öyküsü; Möbius ġeridi Ve
Ünlü Grafiker Escher; ÇeĢitli Sayı Sistemleri;
Dört Renkli Harita Problemi; Öklid-DıĢı
Geometriler; Fermat’nın Son Büyük Teoremi,
Asal Sayılar Ve Paul Erdös.
MAT 213 PROĞ.GĠRĠġ
(Fizik Böl.)
(3 - 3)
Bilgisayarın Yapısı; Bilgisayar Çevre Ünitelerinin
Tanıtılması; Bilgisayarın ġematik Yapısı; Ġkili Sayı
Sistemleri; Onaltılı Sayı Sistemi; Sayı Sistemlerinin
KarĢılaĢtırılması; Dos Komutlarının Tanıtımı Ve
Kullanılması; Çevre Üniteleri; Basıc Programlama
Dilinin Öğeleri; DeğiĢken Tanımlama; BASIC
ArĢiv Fonksiyonları; BASIC Kontrol Deyimleri;
Basıc Fonksiyonları;
Bilgisayar
Kütükleri;
Anakütük; Günlük Bilgi Kütüğü; Rapor Kütüğü;
Sıralı Kütük.
MAT 253 OLASILIK VE ĠSTATĠSTĠK I
(3 2 4)
MAT 254 OLASILIK VE ĠSTATĠSTĠK II (3 2 4)
Olasılık Ve Ġstatistik Tanımı; Cümleler Kuramı;
Permutasyonlar Ve Kombinasyonlar; Olasılığa
GiriĢ; Rasgele DeğiĢkenler Ve Beklenen Değer;
Bazı Kesikli
Olasılık
Dağılımları;
Sürekli
Rasgele
DeğiĢkenlerin Dağılımları; Örneklem
Seçimi.
Verilerin Düzenlenmesi Analizi; Örnekleme
Dağılımları Ve Tahmin Etme Hipotez Testi; KiKareye Dayanan
Önemlilik
Testleri;
Regresyon Ve Korelasyon; Varyans Analizi.
MAT 263 TOPOLOJĠYE GĠRĠġ
MAT 264 TOPOLOJĠK UZAYLAR
(3 0 3)
(3 0 3)
Gösterimler ve terimler; Gerçel Analiz için
Önbilgiler, Gerçel Sayılara bir bakıĢ, Gerçel
Sayılarda
Dizilerle
ilgili
hatırlatmalar,
Fonksiyonlarda
Limit
Kavramı,
Süreklilik
Kavramı; Topolojik Uzay Nedir? Açık Kümeler,
KapanıĢ; KomĢuluklar ve KomĢuluk Sistemleri;
Yakınsak Diziler; Kaba ve Ġnce Topolojiler; Alt
Uzaylar Ve KondurulmuĢ Topolojiler; Taban Ve
Alt Taban; Yerel Taban Kavramları;
Metrik
Uzaylara kısa bir bakıĢ; Metrik Uzaylarda
Süreklilik, Topolojik Uzaylar ve Süreklilik,
Yakınsaklık, Alt Uzaylar; Toplamlar, Çarpımlar ve
Bölüm Uzayları.
To ve T1 Uzaylar, Hausdorff’luk KoĢulu, Düzenli
Tam (amen ) Düzenli Uzaylar; T3 Ve Normal
Uzaylar; Kompaktlığın Tanımı, Örtü, noktasal
sonlu örtü, yerel sonlu örtü ve Yıldızıl sonlu örtü,
Göreli Kompakt Uzay, Sonlu Arakesit Özelliği;
Sayılabilir Kompakt, Yatrıkompakt ve Dizisel
Kompakt Uzaylar; Parakompakt Uzaylar, Birimin
ParçalanıĢı, Metrik ve Metriklenebilir Uzaylar;
Bağlantılı Küme Ve Uzaylar; Düzgün Uzaylar;
Fonksiyon Uzayları; EĢsüreklilik; AscoliTeoremi;
Kompakt
Yakınsama;
Normlu
Uzaylarda
Fonksiyoneller.
MAT 273 ANALĠTĠK GEOMETRĠ I
MAT 274 ANALĠTĠK GEOMETRĠ II
(2 2 3)
(2 2 3)
Uzayda
Kartezyen
Koordinatlar,
Uzayda
Vektörlere, Skaler Çarpım, Vektörel Çarpım ve
Karma Çarpım, Koordinat Eksenlerinin Ötelenmesi
ve Dönmesi, Uzayda Doğrular, Uzayda Düzlemler
Genel
Ġkinci
Derece
Eğrileri,
Konikler,
Determinant Denklemleri, Konikler Üzerine
GenelleĢtirmeler, Uzayda Eğriler, Yüzeyler Ve
Dönel Yüzeyler
MAT 283 ĠLERĠ ANALĠZ I
MAT 284 ĠLERĠ ANALĠZ II
(3 2 4)
GiriĢ sayılar ve kümeler; Tamlık aksiyomu; Gerçek
eksen ve bir boyutlu Euclid uzayı; Dizi; Limit; nboyutlu Euclid uzayı; Dizi limit Rn ve Rn ds seriler;
Kompakt ve bağlantılı kümeler; Yol bağlantılı
sürekli fonksiyonlar; Düzgün sürekli fonksiyonlar.
(3 2 4)
Düzgün Yakınsaklık; Dirichlet ve Abel Ölçütleri,
Kuvvet Serileri; Ġki veya Daha Çok DeğiĢkenli
Fonksiyonlar;
Türevlenebilen Fonksiyonlar;
YönlüTürev; Gradient;
Diverjans;
Rasyonel
Laplasyen; Ortalama Değer Teoremi;
Yüksek
Türevler; Maksimum; Minimum; Ters Fonksiyon
Teoremi; Kapalı Fonksiyon Teoremi; Ġntegral;
Riemann Ġntegrali; Ìntegral Ölçümü Sıfır Olan
Kümeler.
MAT 293 DĠF.DENKLEMLER I
(3 2 4)
GiriĢ Diferansiyel Denklemlerin Sınıflandırılması
Ve Elde EdiliĢleri; Uygulamalı Bilìmlerden
Örnekler; Birinci
Basamaktan
Ve
Birinci
Dereceden Denklemler Ve Çözüm Yöntemleri;
DeğiĢkenlerine
Ayrılabilen
Denklemler
(Homojen)
Bir
Yapımlı Denklemler; Tam
Diferansiyel Denklemler; Ġntegral Çarpanı;
DeğiĢken DeğiĢtirme; Doğrusal Denklem; Bernoulli
Denklemi;
Riccati Denklemi; Geometrik
Uygulamalar Yörüngeler; Birinci Basamaktan
Yüksek Dereceden Denklemler; Tekil Çözüm; Zarf;
X'e Göre Çözülebilen Denklemler; Y’ye Göre
Çözülebilen Denklemler; Lagrange Ve Clarìaut
Çözülebilen Denklemler; Lagrange Ve Clarìaut
Denklemleri; Varlık Ve Teklik Teoremi;
MAT 294 DĠF.DENKLEMLER II
(3 2 4)
Yüksek Basamaktan Doğrusal Denklemler;
Doğrusal Bağımsızlık; Sabit Katsayılı Ġkinci
Tarafsız Denklemler; Sabit Katsayılı Ġkinci Taraflı
Doğrusal Denklemler; DeğiĢen
Parametreler
Yöntemi; DeğiĢken
Katsayılı
Denklemler;
Cauchy-Euler Denklemi; Basamağın DüĢürülmesi;
Operatörün Çarpanlarına Ayrılması Yöntemi;
Yüksek
Basamaktan
Doğrusal
Olmayan
Denklemler; DeğiĢkenlerden Birini Ġçermeyen
Tipten Denklemler; EĢ
Boyutlu
Denklemler;
Sarrus Yöntemi; Diferansiyel Denklem Takımları;
Birinci Basamaktan Sabit Katsayılı Doğrusal
Denklem Takımı; Yüksek Basamaktan
Sabit
Katsayılı Doğrusal Denklem Takımları; Denklem
Takımları Ġçin Varlık Teklik Teoremleri; Kuvvet
Seriler Ġle Çözüm; Laplace DönüĢümü Ve Laplace
DönüĢümüyle Sabit Katsayılı Denklemlerin
Çözümü.
MAT 296 TEMEL BĠLGĠ TEKNOLOJĠ
(2 0 2)
Bilgisayar Tarihçesi Ve Bilgisayar Türleri,
Donanım Ve Yazılım Sistemi, Sayı Sistemleri,
Sayısal Bilgisayarların Yapısı, RAM, ROM,
EPROM Bellekler, Kodlama Sistemleri, GiriĢÇıkıĢ Sistemleri, Yardımcı Bellekler, ĠĢletim
Sistemleri, WĠNDOWS ĠĢletim Sistemleri; Yazım
Editöründe
Metin
Dosyası
OluĢturularak
Düzenlenmesi Ve Biçim Özelliklerinin Verilmesi
Ġle Temel Bilgisayar Bilgilerinden Yazılım Ve
Donanımın Genel Yapısının Ġncelenmesi,
MAT 335 MATEMATĠKSEL ĠSTATĠS. I (3 - 3)
MAT 336 MATEMATĠKSEL ĠSTATĠS. II (3 - 3)
Cümleler Cebiri; Olasılık Ölçüsü; Olasılık Uzayı;
Olaylar;
Olayların
Bağımsızlığı;
Rasgele
DeğiĢkenler; Dağılım Fonksiyonları; Sürekli
Rasgele DeğiĢkenler; Dağılım Fonksiyonları;
Sürekli Rasgele DeğiĢkenlerin
Fonksiyonunun
Olasılık Dağılımı.
Rasgele Vektörler; Marjinal Dağılımlar; Rasgele
DeğiĢkenlerin Bağımsızlığı; Rasgele Vektörlerin
DönüĢümlerinin
Olasılık
Dağılımları;
Karakteristik Fonksiyonlar; Üretici Fonksiyonlar
Ve Bazı EĢitsizlikler.
MAT 355 KISMĠ DĠF.DENKLEMLER I
MAT 356 KISMĠ DĠF.DENKLEMLER II
(3 - 3)
GiriĢ; Denklemlerín Sınıflandırılması; Gösterimler;
Denklemlerin Elde EdiliĢleri; Varlık Ve Teklik
Teoremleri; Birinci Basamaktan Denklemlerin
Çözüm Yöntemleri;
Lagrange
Yöntemi;
Çözümler Ġçin Yöntemleri; Lagrange Yöntemi;
Çözümler
Ġçin Basamaktan Yarı Doğrusal
Denklemler Ġçin Cauchy Problemi; Genel Birinci
Basamaktan
Denklemler
Ġçin
BağdaĢabilir
Sistemler; Charpite Yöntemi; Genel Birinci
Basamaktan Denklemler Ġçin Cauchy Problemi
Ve Cauchy Karakteristikler Yöntemi; Özel Tip
Denklemler Ve Ġndirgeme.
(3 - 3)
GiriĢ; Ġkinci Basamaktan Ġki Bağımsız DeğiĢkenli
Doğrusal Denklemler; Sabit Katsayılı Denklemler;
Çarpanlarına Ayrılabilir Operatörler; N-Bağımsız
DeğiĢkenli
Doğrusal
Ġkinci
Basamaktan
Denklemler; Üstel Tipten Çözümler; Normal
ġekiller; Ġki Bağımsız DeğiĢkenli Hemen Hemen
Doğrusal
Denklemlerin
Sınıflandırılması;
Hiperbolik
Denklemler; Karakteristik Eğriler;
Parabolik Denklemler; Eliptik Denklemler; Ġki
Bağımsız DeğiĢkenli Doğrusal Denklemler Ġçin
Cauchy Problemi Cauchy-Kowalsky
Teoremi
(Özel Hal) Karakteristik Eğrilerin Önemi;
DeğiĢken Katsayılı Denklemler Ġçin Monge
Denklemleri; Adjoint Operatör; Green Formülü;
Self Adjoint Operatör; Dalga Denklemi; Isı
Denklemi;
Laplace Denklemi Çözümleri Ve
Fiziksel Yorumlar.
HTML Döküman Ġçinde Sayaç Kullanımı HTML
Döküman Ġçinde Basit Javascript Kullanımı
MAT 365 SAYILAR KUR.GĠRĠġ
MAT 366 SOYUT CEBĠRE GĠRĠġ
(4 0 4)
(4 0 4)
Tam Sayılar; Bölünebilme; Kalanlı Bölme Ve
Asal Çarpanlara AyrılıĢ; Teorik Sayı Fonksiyonları;
Kongrüanslar Ve Kongrüans Denklemleri; Ġlkel
Kökler ve Ġndisler; Kuadratik Kalanlar ve
Kuadratik olmayanlar, Kuadaratik Ġkiyanlılık, Jacob
i Sembolü, Asalımsılar ve Euler asalımsıları;
Sürekli Kesirler, Ondalık Kesirler, sonlu ve sürekli
kesirler, irrasyoneller, periyodik Sürekli Kesirler ve
Sürekli Kesirlerle Çarpanlara Ayırma; ġifreleme ve
temel ġifreleme Algoritmaları,Basit ġifreleme
Yöntemleri, Karakter ġifreleme ve Stenografi.
Temel kavramlar, bağıntılar, fonksiyonlar, iĢlemler
ve genel cebirsel yapılar; Gruplar, altgruplar, Zn,
Zn*, Dn ve Sn Grupları; Devirli gruplar,normal
altgruplar, Bölüm grupları; Halkalar Teorisine GiriĢ
Ve Temel Kavramlar; Alt Halkalar; Bazı Özel
althalkalar, Benzeryapı, EĢyapı ve Özyapı
Kavramları, Ġdealler Ve Bölüm Halkaları; Polinom
Halkaları; Simetrik Fonksiyonlar, Çok değiĢkenli
polinomlar, diskriminant ve rezültant; 2, 3 ve 4üncü derecede denklemler; vektör uzayları,
Cebirsel, Normal ve Galois GeniĢlemeleri.
MAT 375 KARMAġIK FONK.KUR. I
MAT 376 KARMAġIK FONK.KUR. II
(3 2 4)
(3 2 4)
Kompleks Sayıların Tanımı Ve Cebirsel Yapısı;
Kompleks
Sayıların
Geometrisi;Limit
Ve
Süreklilik, Diferansiyellenebìlme,
CauchyRiemann Denklemleri, Analitik Fonksiyonlar;
Kompleks Fonksiyonların Tanımı Ve Basit
Özellikleri; Kompleks
DönüĢümlerin Temel
Özellikleri, Doğrusal, Kuvvet, Çift Doğrusal, Üstel
Ve Logaritmik DönüĢümler; W=Sin Z Ve W=Cos
Z DönüĢümleri
Kompleks Ġntegrasyon; Yol Ve Bağlantılılık
Kavramları; Çizgi Ġntegraller; Çizgi Ġntegralin
Hesabı; Kompleks Ġntegral, Cauchy
Teorisi,
Analitik Fonksiyonların Ġntegralleri; Cauchy
Teoremi; Cauchy Ġntegral Teoremi; Morera
Teoremi, Kompleks Kuvvet Serileri, Kompleks
Sayıların Dizi Ve Serileri, Kuvvet Serisi Olarak
Analitik Fonksiyonlar, Analitik Fonksiyon Olarak
Kuvvet Serileri, Laurent Serileri, Rezidüler,
Analitik Fonksiyonların Tekil Noktaları Ve
Sıfırları, Rezidü Teorisi , Sonsuz Ġntegraller.
MAT 385 GERÇEL ANALĠZ I
MAT 386 GERÇEL ANALĠZ II
(3 0 3)
(3 0 3)
Kümeler Ve Bağıntılar; Reel Sayılar Sistemi;
Lineer Uzaylar; Metrìk Uzaylar; Sabit Nokta
Teoremi Ve Uygulamalar.
Lebesque Ġntegral; Normlu Lineer Uzaylar;
YaklaĢımın Temel Teoremleri; Stieltjes Ġntegraller
Ve Ġç Çarpım Uzayları.
MAT 397 INTERNET VE HTML PROG. (2 2 3)
Internet Nedir? TCP/IP Nedir? Internete Kimler
Dahildir? Kaç Tane Bilgisayar Internet'e Bağlıdır?
Kaç KiĢi Internet Kullanıyor? Internet Ne Sunar?
Internet Yoluyla Alabildiğim Bu Bilgileri,
Programları Kimler Koyar? Bunları Alıyorum Ama,
Para Ödemem Gerekir Mi? Freeware, Shareware,
Public Domain Gibi Kavramlar Ne Anlama Gelir?
Internet'e EriĢim Nasıl Olur? Internet Adresi Nedir?
Domain Ġsmi Ve IP Numarası Ne Demektir? EMail (E-Posta) Nedir? E-Posta Adresi Nedir?
Adresini Bildiğim Birisine Nasıl E-Posta
Gönderirim? E-Posta Programlarında Görülen
"From, To, Subject, Cc, Bcc, Forward To: " Gibi
Kısaltmalar Ne Anlama Gelir? Nickname (Takma
Ad) Nedir? Signature (Imza) Nedir? Nasıl
Kullanılır? Folder (Notebook) Nedir? Attachment
(EklenmiĢ Dosya) Nedir? HTML Dilinin En Temel
Elemanı : Döküman Biçimleme Belirteçleri (TAG)
HTML Dökümanın Genelinde Etkili Ve Döküman
Ġçinde Doğrudan Görünmeyen Belirteçler HTML
Döküman Ġçinde LINK Kullanımı Temel HTML
Komutları/Belirteçleri
Sayfa
Arka
Plan
Resimleri/Renkleri Ve Metin Ġçinde Renk
Kullanımı Listeler Basit Tablolar Form Kullanımı
MAT 398 OFFICE PROGRAMLARI
(2 2 3)
WORD: Belge Düzenleme, Sıkça Kullanılan Araç
Çubukları, Karakter Ve Paragraf Biçimlendirme,
Paragrafları Girintileme, Belgeyi Yazdırma, Yazım
Ve Dilbilgisi Denetimi, Üstbilgi Ve Altbilgi
Yaratma, Dipnot Ekleme, Bir Tablo Yaratma,
Büyük Boyutlu Tablo Yaratma, Tablo Düzeni
EXCEL: ÇalıĢma Sayfasını Düzenleme, Formül
Yazma, Çok Sayıda Listeyi BirleĢtirme, Grafik
OluĢturma Süzgeç Uygulama, Veri Düzenleme
Üzerine ĠĢlemler, ÇalıĢma Sayfasını BaĢkalarıyla
PaylaĢma, Makro
POWERPOINT: Sunu Düzenleme, ġablonlar, Ses
Ve Video Ekleme, Slayt Gösterisi Hazırlama,
Sunuyu TaĢıma, Internet Sunusu Hazırlama, Sunu
PaylaĢımı
MAT 405 FĠYATLANDIRMA MODELL. (2 0 2)
MAT 406 MATEMATĠK SEÇME KONUL.(2 0 2)
Ölüm Sigortasında Ġleri Ġstatistiksel Metodlar,
Fiyatlandırma, Kaynak Tüketme Ve Reinsurans
Yöntemleri.
Ulusal Ve Uluslararası Popüler Problemleri
Tanıtma, Bilinen Ġlginç Bazı Problemlerin
Çözümlerini Ve Uygulanan Yöntem Ve GörüĢleri
Ġrdeleme.
MAT 411 ENĠYĠLEME KURAMI
(2 0 2)
Normlu Lineer ve Hilbert Uzayları, En-Küçük
Kareler Kestirimi, Dual Uzaylar, Hahn Banach
Teoreminin Geometrik ġekli, Lineer Operatörler Ve
EĢlekleri,
Hilbert
Uzaylarında
Eniyileme,
Fonksiyonellerin Eniyilemesinin Yerel Ve Global
Teorisi, Constrained Ve Unconstrained Haller.
MAT 417 MATEMATĠK TARĠHĠ I
(2 – 2)
Mısır Ve Mezopotamyada Matematik, Ġyonya Ve
Pisagoryanlar, Zeno Paradoksları Ve Eski Çağ,
Plato, Aristo, Aleksadıryalı Öklit, ArĢimed,
Apolonyus Ve Diyofantın Matematik ÇalıĢmaları,
Çin Ve Hint De Matematik.
MAT 437 MAT. ÖĞRETĠM YÖNT. I
MAT 418 MATEMATĠK TARĠHĠ
II
(2 – 2)
Rönesans Ve Ġslam Etkisinde Matematik, Kübik
Denklem Ve Sonuçları, Logaritmanın BulunuĢu,
Fermat Ve Dekart Çağı, Limit Kavramının
GeliĢimi, Newton Ve Leibniz, Euler Çağı, Gauss
Ve Cauchy Katkıları, Öklit Olmayan Geometriler,
Analizin AritmetikleĢtiriliĢi, Soyut Cebirin DoğuĢu,
20-Nci Yüzyılda Durum.
(2 0 2)
Öğretme Stratejisi Ve Yöntem Kavramı, ÇalıĢma
Disiplini Olarak Matematiğin GeliĢimi, OrtaÖğretimde Matematiğin Öğretilmesi Ġlkeleri Göz
Önünde Tutularak Farklı Öğretme Yöntemlerinin
Sınıf Ġçinde Uygulanması, Sınıf Gözlemlerini
Kapsayan Öğretme Pratiği Ve Alan Deneyimi
Kazandırma, Sınıf KoĢullarının Düzenlenmesi,
Öğretme Ġçin Hazırlanacak Planın GeliĢtirilmesi.
FĠZ 439 FĠZĠKTE SEÇME KONULAR
(2 – 2)
Fizik Bölümü Tarafından, Matematik Öğrencilerine
Günlük YaĢamda Sıklıkla KarĢılaĢılan Fiziksel
Olayların Tanıtımı Ve Yine Günlük YaĢamda
Sıklıkla KarĢılaĢılan Özellikle Elektriksel Bazı
Fiziksel Becerilerin Kazanılmasına Yönelik Ölçüm
Aletlerinin
Kulanımı
Ve
Uygulamalarda
KarĢılaĢılabilecek Risk Ve Zorluklar.
MAT 445 BAĞIMSIZ ÇALIġMA
(2 0 1)
Öğrencilerin, Bir DanıĢman Öğretim Üyesi
Rehberliğinde, DanıĢman Tarafından Önerilen
Veya Öğrencinin Kendisinin Belirleyebileceği Bir
Veya Daha Çok Konuda, DeğiĢik Kaynaklardan
Yararlanmak Suretiyle, Bir Yarıyıl Ġçinde Yapacağı
AraĢtırma-Ġnceleme Sonuçlarını, Yarıyıl Sonunda,
Yazılı Bir Rapor Halinde Sunmalarını Amaçlayan
ÇalıĢma.
MAT 446 LĠSANS TEZĠ
(2 0 1)
Öğrencilerin, I. Yarıyılda, DanıĢman Öğretim Üyesi
Rehberliğinde MAT 497 Bağımsız Çalışma Adı
Altında Sürdürdükleri AraĢtırma Faaliyetlerine
Devam Etmeleri, Elde Ettikleri Sonuçların
Kurallara Uygun Bir Biçimde Bir Mezuniyet Tezi
Haline Getirtilmesi Ġle Yarıyıl Sonunda Bölüm
Öğretim Üyelerinden OluĢacak Bir Jüri Veya
DanıĢman Önünde Sözlü Olarak Sunma Ve
Savunmalarını Amaçlayan Bilimsel ÇalıĢma.
,MAT 447 RĠSK ANALĠZĠ
(2 0 2)
MAT 448 AKTÜERYA TEKNĠKLERĠ
(2 0 2)
Riskin Tanımı, Risk Artması, Riskin Ölçümü Ve
Risk Aversiyonu, Kayıp Dağılımları Modellenmesi,
Temel Fiyatlandırma Ve Kaynak Teknikleri,
Sigorta, Ferdi Ve Toplu Risk Kuramı, Güvenilirlik
Ve Ruin Teorisi.
Faiz Teorisi Ve Ġskonto Prensipleri, YaĢama Ve
Ölme Olasılıkları Ġçin Hayat Tabloları, Ölüme
ĠliĢkin Olasılık Modelleri, Hasar- Risk Süreci,
YaĢam Ve Ölüme Bağlı Sigortalar, Sigorta Türleri
Ve Net Prim Hesaplanması, Poliçe Değer Kavramı.
MAT 457 FONKSÌYONEL ANALĠZ I
MAT 458 FONKSÌYONEL ANALĠZ II
(3 - 3)
(3 - 3)
Metrik Ve Topolojik Uzaylar, Metrik Ve
Yarımetrik Uzaylar, Tam Metrik Uzay, Bazı
Metrikler Ve Topolojik Kavramlar, Metrik Ve
Topolojik Uzaylarda Sürekli Fonksiyonlar,
Kompakt Kümeler, Lineer Ve Lineer Metrik
Uzaylar, Metrik Liner Uzay , Topolojik Lineer
Uzaylar
Normlu Lineer Uzaylar, Yakınsaklık Ve Tamlık,
Lineer Operatörler Ve Fonksiyoneller, BanachSteinhaus Teoremi, Hilbert Uzayı, Ġç Çarpım Ve
Hilbert Uzayı, Ortonormal Kümeler
MAT 477 UYGULAMALI MATEMA. I
(2 2 3)
MAT 478 UYGULAMALI MATEMAT. II (2 2 3)
Eğrísel Ġntegraller; Green Teoremi; Gauss Teoremi;
Diverjans Teoremi Ve Uygulamaları; Çok Katlı
Ġntegrallerin Alan, Hacim, Kütle, Ağırlık Merkezi
Ve Eylemsizlik
Momenti
Hesaplarında
Kullanılması; Pappus Teoremleri Ve Uygulamaları;
Fourìer Serileri.
Özdeğer Problemleri; Sturm-Liouville Sistemlerí;
Dik
Fonksiyon
Uzayında
Fonksiyonların
Özdeğer Cinsinden Seriye Açılımları; Homojen
Olmayan Sturm-Liouville Sistemleri Ve Green
Fonksiyonu; BaĢlangıç Ve
Sınır
Değer
Problemlerinin Green Fonksiyonu
Yardımıyla
Çözümü;
Laplace DönüĢümleri Ve Laplace
DönüĢümleri
Yardımıyla
Adi
Ve Kısmi
Diferansiyel Denklemler Ġçin BaĢlangıç Ve Sınır
Değer
Problemlerinin
Çözümü;
Fourier
DönüĢümleri Ve Uygulamaları.
MAT487 C PROGRAMLAMA
MAT488 VERĠ TABANLARI
(2 0 2)
Kullanılan DeğiĢkenler, Veri Tipleri, Main, Define,
Fonksiyonlar, Printf /Scanf Komutu, While
Döngüsü, For Döngüsü, Ġf Komutu, BreakContinue, Switch Komutu, Goto, Diziler, Pointer,
Dosya ĠĢlemleri, Fopen, Fclose Komutları
(2 0 2)
Veri Taban Yapıları, Create,List, Structure, Edit,
Browse, Replace, Locate, Say-Get , Delete, Find,
Say, Get Komutları, Fonksiyonlar, Set Yapıları,
Fields Türleri, DeğiĢkenler, Report Form, Screen
Formları, Program Dosyaları
BĠY 498 YAġAM BĠLĠMĠ
(2 – 2)
Matematik Öğrencilerinin Biyolojik YaĢamı
Tanımaları Amacıyla, YaĢamı OluĢturan Öğeler,
Yakın Çevremizde Bulunan Yararlı Veya Zararlı
Bitki Türlerinin Tanınması, Genetik, Çevre Ve
Kirlilik Gibi Diğer Bazı Seçme Konular.
KĠM 498 YAġAM KĠMYASI
(2 – 2)
Bilinmesi Zorunlu Temel Kimya Ġle Hayati Kimya
Ve Ġnsan Kimyasının Tanıtılması, Kimyanın
YaĢamdaki Rolü Ve Öneminin Kavranması,
Kimyadaki Matematik Hakkında Bilinen Ve Olası
Uygulama Alanları, Çevremiz Ve Kimyası,
Erozyon Ve Kirlilik Ve Bunların Önlenmesi
Yöntemleri.