7-moment-tork - muhendislik bilgileri

7-MOMENT-TORK
M.Feridun Dengizek
MOMENT-TORK
Bir cisme ağırlık merkezinden geçmeyen bir kuvvet
etki ederse o kuvvet o cismi ağırlık ekseni
etrafında döndürmeye çalışır.
Bu etkiye Moment veya Tork denir.
(Türkiye de genellikle bu etki yapı elemanları üzerinde ise Moment, makina elemanları üzerinde ise
Tork olarak adlandırılır. Biz derslerimizde Moment terimini kullanacağız)
MOMENTİN BÜYÜKLÜĞÜ
Moment esas olarak kuvvetin dönme eksenine olan dik
mesafesi ile çarpımı olarak tanımlanır.
M=F*d
F 7.1
Bkz şekil 1
Eğer kuvvet belli bir açı ile uygulanıyorsa
M=F*d*sinϴ
F 7.2
Bkz. Şekil2
Eğer uygulanan kuvvet dönme noktasından geçiyorsa
M= d*F*sin 0  M=0
Bkz Şekil 3
MOMENTİN YÖNÜ
Momentin yönü sağ el kuralı ile belirlenir. Sağ elin
baş parmağı yukarıyı gösteriyor ve diğer
parmaklar kapalı durumda iken,
parmaklar kuvvetin yönünü, baş parmak ise
momentin yönünü gösterir. Bkz. Şekil 4
Diğer bir tanım;
İki boyutlu bir düzlemde kuvvet cismi saat
yelkovanı istikametinin tersi yönünde
döndürmeye çalışıyorsa moment iki boyutlu
düzleme bakana (dışa) doğru olur.
Bkz şekil 5
İki boyutlu düzlemde momentin yönü dışa doğru
ise yuvarlak içinde nokta, içe doğru ise
yuvarlak içinde X olarak da gösterilir.
Bkz şekil 6
İki boyutlu düzlemde saat yelkovanının tersi yönde
döndürmeye çalışan momentler pozitif (+)
Saat yelkovanı yönünde döndürmeye çalışan
momentler ise negatif (-) kabul edilir.
(+) Moment
(-) Moment
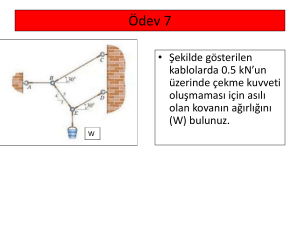
ÖRNEK PROBLEM 7.1
Yandaki elemanlarda ortaya çıkacak moment
büyüklüklerini bulunuz.
Şekil 6
Şekil 6 M= -0.75*50N  M= -37.5 N-m
Şekil 7 M= 7*(4-1)  M= 21 kN-m
Şekil 7
Şekil 8 M= 1*sin45*60  M= 42.4 kN-m
Şekil 8
ÖRNEK PROBLEM 7.2
Yandaki borunun duvardan çıktığı O noktasında 50N kuvvetin
etkisi ile meydana çıkacak moment büyüklüğünü
bulunuz.
ÇÖZÜM 7.2
Bu problemin çözümü için gerekli bilgi mühendislik
mekaniğinden çok geometridir
Önce O noktasından kuvvet doğrultusuna dik mesafe d
bulunmalıdır.
Şekil 9
d=y*sin60
y=u-v
u=100+200*cos45+100 = 341.42 mm
v = 200*sin45 / tan60 =81.65 mm
 y=341.42-81.65=259.7 mm
 d=259.7*sin60 d=224.9 mm=0.225m
M=F*d
 M=50*(-0.225)  M=-11.25N-m
Kuvvet boruyu O noktası etrafında saat yelkovanı yönünde
döndürmeye çalıştığı için moment negatif değer alır
Şekil 10
MOMENTLERİN TOPLANMASI
Düzlemsel planda aynı eksen etrafında etkin
momentler cebirsel olarak toplanabilirler.
ΣMo=ΣFd
Yandaki şekil için
ΣMo= - F1d1 + F2d2 +F3d3
Toplama işleminin sonucu pozitif çıkarsa toplam
moment saat yelkovanı istikametinin tersi
yönünde,
negatif çıkarsa moment saat yelkovanı
yönünde etkin demektir.
Şekil 11
ÖRNEK PROBLEM 7.3
Yandaki borunun duvardan çıktığı O noktasında
yandaki şekilde belirtilen kuvvetlerinin etkisi ile
meydana çıkacak moment büyüklüğünü bulunuz.
ÇÖZÜM 7.2
O noktasına her kuvvet doğrultusuna dik mesafeler
bulunmalı ve kuvvetler ile çarpımları toplanmalıdır
ΣM=ΣF*d
ΣM=500*(1+2+2.5*cos45)-(300*(2.5*sin45)-(600*1)
 ΣM= -1253.5 N-m
Şekil 12
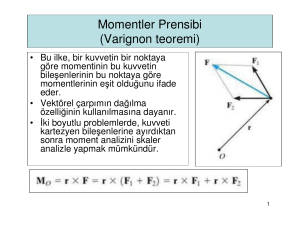
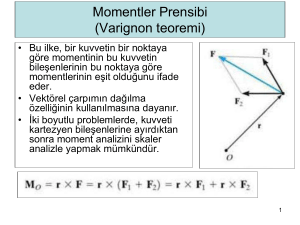
VEKTÖRLERİN ÇAPRAZ ÇARPIMI
(CROSS PRODUCT)
Konum vektörleri konusunu işlerken vektörlerin nokta
çapımını anlatmıştık.
Nokta çarpımında iki vektörün çarpılması ile skalar bir
büyüklük elde edildiğini görmüştük.
Bu derste ise vektörlerin çapraz çarpımı ile nasıl bir başka
vektörel değer elde edildiğini anlatacağız.
C  AXB
F 7.3
Çapraz vektör çarpımında çıkan vektörün büyüklüğü her
iki vektörün skalar büyüklüklerinin aradaki açının sinüsü
ile çarpımı kadar, yönü ise sağ el kuralına uygun olarak
iki vektörün aralarında oluşturduğu düzleme dik olan ve
kesiştikleri noktadan başlayan birim vektör
doğrultusundadır.
 C  A * B * sin  * u
Şekil 13
F 7.4
ÇAPRAZ ÇARPIM KANUNLARI
Çapraz çarpım kanunlarının nokta çarpım kanunlarından en önemli farkı çapraz
çarpımın değişme özelliğinin bulunmamasıdır.
ÇAPRAZ ÇARPIM KANUNLARI
• Değişme özelliği  AXB= - BXA
• Çarpma özelliği  a(AXB)= (a*A)XB = AX(a*B) = (AXB)*a
• Dağıtım özelliği AX(B+C)= (AXB)+(AXC)
Yandaki resimde görüldüğü gibi A vektörü B vektörü
ile çapraz çarpıldığında C vektörünün yönü yukarı
doğru olurken, B vektörü A ile çarpılırsa C
vektörünün yönü ters tarafa doğru gerçekleşir.
Şekil 14
KARTEZYEN VEKTOR FORMÜLASYONU
C  AXB  A * B * sin  * u
ϴ=900  Sin90=1
 C  AXB  A * B * (i  j  k)
Kartezyen vektör formülleri
yukarıdaki tanımın sağ el kuralına
göre çapraz çarpımı ile elde
edilebilir.
ixj=k
j x i = -k
Şekil 15
Aynı yöndeki vektörlerin çapraz
çarpımı ise her zaman sıfırdır.
ixi=0
jxk=i
k x j = -i
kxi=j
i x k = -j
jxj=0
kxk=0
DİKKAT: Vektörlerin nokta çapımında ise aynı
notasyonlu vektörler çarpımı 1 diğerleri ise
sıfırdır
C  AXB
 C=(Axi +Ay j + Azk) X (Bxi + By j +Bzk)
C= (Axi Bxi +Axi Byj +Axi Bzk ) + (Ayj Bxi + Ayj Byj + Ayj Bzk) + (Azk Bxi +Azk Byj +Azk Bz k)
C= AxBx (ixi) + AxBy(ixj) + AxBz(ixk) + AyBx(jxi) + AyBy(jxj) + AyBz(jxk) + AzBx(kxi) + AzBy(kxj) + AzBz(kxk)
Bir önceki slaytta belirtilen kartezyen vektör çapraz çarpım kurallarını uygularsak
 C= AxBx (0) + AxBy(k) + AxBz(-j) + AyBx(-k) + AyBy(0) + AyBz(i) + AzBx(j) + AzBy(-i) + AzBz(0)
C=i(AyBz-AzBy) + j(AzBx- AxBz) + k(AxBy- AyBx)
y eksenindeki (j notasyonlu) terimlerin yerini değiştirirsek

C=AXB= i(AyBz-AzBy) - j(AxBz- AzBx) + k(AxBy- AyBx)
F 7.5
HATIRLATMA
Bu noktada Matrixlerin determinantını bulmayı hatırlayalım
3X3 lik bir matrix determinantı
3X3 lik matrix determinantı F 7.5 de bulmuş olduğumuz.
C=AXB= i(AyBz-AzBy) - j(AxBz- AzBx) + k(AxBy- AyBx)
Çapraz çarpım vektörünü ifade için uygundur.
i.......... ... j.......... ... k
C  AXB  A x....... A y....... A z  i(A y Bz  A z By )  j(A x Bz  A z Bx )  k (A x By  A y Bx )
Bx........ By........ Bz
Böylece iki vektörün çapraz çarpımının daha kolay algılanabilir
olmasını sağlamak için determinant form kullanılmaktadır.
i.......... ... j.......... ... k
AX B  A x....... A y....... A z
Bx........ B y........ Bz
F 7.6
VEKTÖRLERİN ÇAPRAZ ÇARPIMININ
MOMENT BULUNMASI İÇİN UYGULANMASI
Moment büyüklüğünün kuvvet ile kuvvete dik uzaklığın
çarpımı, yönünün ise sağ el kuralına göre saat
yelkovanı yönünün tersi yön için pozitif yön olarak
değerlendirildiğinden bahsetmiştik.
M=F*r*sinϴ= F*d
Eğer r vektörü moment eksenine dik bir düzlemde değil ise
böyle problemlerin çözümünde çapraz çarpım
uygulanmalıdır.
AKTARILMA PRENSİBİ
Bir eksen etrafında etkin kuvvetin eksene uzaklığı birden
fazla gözükebilir. Bkz. Yan şekil. Ancak O eksenine dik bir
düzlemde bu uzaklıkların dikey bileşenleri aynı olduğundan
Moment sabit kalır. Böylece
Mo= r1*F = r2*F= r3*F
Bu özelliğe bir kuvvetin aktarılma prensibi denilir
VEKTÖRLERİN ÇAPRAZ ÇARPIMININ
MOMENT BULUNMASI İÇİN UYGULANMASI
Üç boyutlu düzlemde etkin kuvvet vektörü F ile kuvvet kolu vektörü
r değerlerinin (Bkz şekil 16) çapraz çarpım yolu ile bu iki
vektörün oluşturduğu düzleme dik olan O ekseni etrafında
oluşan momentin bulunması için önce r ve F vektörleri
kartezyen bileşenlerine ayrılmalıdır. (Bkz. Şekil 17)
Sonra matrix formatında yerleştirilerek determinant formatından
yararlanılarak Moment bulunur
Şekil 16
i.......... ... j.......... ... k
M o  rX F  rx.......... ry.......... .. rz
F 7.6
Fx........ Fy.......... Fz
Şekil 17
M o  i(ry Fz  rz Fy )  j(rx Fz  rz Fx )  k (rx Fy  ry Fx )
F 7.5
Eğer bir nokta etrafında birden fazla kuvvet ve kuvvet
kolu etkin ise (Bkz şekil 18) toplam moment
Mo=Σ(rXF)
olur
F 7.7
Şekil 18
ÖRNEK PROBLEM 7.4
Yandaki borunun duvardan çıktığı O noktasında
yandaki şekilde belirtilen kuvvetin etkisi ile
meydana çıkacak moment büyüklüğünü
bulunuz.
ÇÖZÜM 7.4
Önce kuvvet kartezyen koordinatlarda yazılmalıdır.
O(0,0,0) A(1,4,0) B(1,4,2) C(5,0,0)
Şekil 19
FBC  F * u BC
u BC 
rBC
rBC
rBC  rC  rB
rB  1i  4 j  2k
rC  5i
rBC  4 2  (4) 2  (2) 2  rBC  6
rBC  rC  rB
 u BC 
 rBC  4i  4 j  2k
u BC  0.667i  0.667 j  0.33k
 FBC  120 * (0.667i  0.667 j  0.333k )
 FBC  80i  80 j  40k
4i  4 j  2k
6
ÇÖZÜM 7.4 Devamı
i.......... ...... j.......... ........ k
rC  5i
M o  rC X FBC  rCx .......... rCy.......... ..... rCz
FBCx ........ FBCy .......... FBCz
i.......... ...... j.......... ..... k
 M o  5.........0.........0
80....  80...  40
Şekil 19
M o  i(ry Fz  rz Fy )  j(rx Fz  rz Fx )  k (rx Fy  ry Fx )
Mo  i (0 * (40))  (0 * (80)   j (5 * (40))  (0 * (80)   k(5 * (80))  (0 * 80)
Mo   j (200)  0   k(400)  0
 M o  (200 j  400k) N  m
Aynı problemi rB üzerinden çözersek
rB  1i  4 j  2k
i.......... ...... j.......... ..... k
 M o  1.........4.........2
80....  80...  40
Mo  i (4 * (40))  (2 * (80)   j (1* (40))  (2 * (80)   k(1* (80))  (4 * 80)
M o  i (160)  (160)   j (40)  (160)   k(80)  (320)
 M o  (200 j  400k) N  m
Aynı sonuca ulaşılır
ÖRNEK PROBLEM 7.5
F1=(100i-120j+75k)lb
F2=(-200i +250j+100k)lb
Olarak verilmiş sistemde borunun duvardan çıktığı O noktasında
yandaki şekilde belirtilen kuvvetlerin etkisi ile meydana çıkacak
moment büyüklüğünü bulunuz.
ÇÖZÜM 7.5
Önce kuvvetlerin etki ettiği noktanın konum vektörü yazılır
rA  4i  5 j  3k
Kuvvetler aynı noktadan etki ettiği için kuvvetler toplanarak tek
bir kuvvete dönüştürülür
 F  F  F  (100i  120 j  75k)  (200i  250 j  100k)
  F  100i  130 j  175k
1
2
i.......... .......... .... j.......... ........ k
M o  rA X F  4..............5...........3
 100.....130......175
Mo  i (5 *175)  (3 *130   j (4 *175)  (3 * (100)   k(4 *130)  (5 * (100)
M o  (485i  1000 j  1020k )lb  ft
Şekil 20
VARIGNON PRENSİBİ
Daha önce düzlemsel vektörlerde moment büyüklüğünün (M) kuvvet (F)X kuvvet
doğrultusuna dik mesafenin (d) çarpımı olduğunu görmüştük. (Bkz. Şekil 21)
M=F*d
Waringon isimli fizikçi göstermişdir ki bu aynı zamanda kuvvetin dik bileşenlerinin x ve y
eksenlerine olan uzaklıkları çarpımlarının farkına eşittir.
M  Fy * x  Fx * y
F 7.8
Bu formülasyon ile kuvvet doğrultusuna dik mesafenin belirlenmesi zorluğu ortadan
kalktığı için M=F*d yerine kullanılabilir
PROBLEM 7.2 NİN WARIGNON METODUNA GÖRE ÇÖZÜMÜ
Warignon metoduna göre kuvvete dik mesafenin bulunmasına gerek yoktur
Fx=F*cosϴ
 Fx= 50*cos60  Fx=25N
Fy=F*sinϴ
 Fy= 50*sin60  Fy=43.3N
M  Fx * y  Fy * x
X=100 + 200*Cos45 +100  x=341.42 mm
Y=200*sin45  141.42 mm
M=25*141.42 - 43.3*341.42
M= -11,250 N-mm
M= -11.25 N-m