Vektör Analizi

ELEKTROMANYETİK ALAN TEORİSİ
Hafta
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Konu
Vektör Analizi
Koordinat Sistemleri ve Dönüşümler
Elektrik Yükleri ve Alanlar
Elektriksel Akı ve Gauss Yasası
Diverjansın Fiziksel Anlamı ve Uygulamaları
Statik Elektriksel Alanın Endüstriyel Uygulamaları
Elektriksel Potansiyel
Enerji
Akım ve Akım Yoğunluğu
İletkenler ve Sınır Şartları
Dielektrikler ve Sınır Şartları
Kapasitör ve Uygulamaları
Laplace ve Poisson Denklemlerinin Çözüm Tahminleri
Görüntü Metodu
Vektör Analizi
Alan uzay ve zamanda gözlenebilir bir niceliğin veya büyüklüğün
süreklilik gösteren dağılımı olarak tanımlanabilir.
Skaler ve vektörel alanlar
Vektör Analizi
Elektrik alan şiddeti (E) boş uzaydaki elektrostatik alanların
açıklanabilmesi için gereken tek vektör olup birim test yüküne etkiyen
elektrik kuvveti olarak tanımlanır.
Elektrik akı yoğunluğu (D) malzeme ortamında elektrik alan
çalışmasında kullanışlıdır.
Manyetik akı yoğunluğu (B) boş uzayda manyeto statik (kararlı
elektrik akımlarının etkisi) tartışmasında gereken tek vektördür ve
belirli bir hızla hareket eden yük üzerine etkiyen manyetik kuvvet ile
ilişkilidir.
Manyetik alan şiddeti (H) malzeme ortamında manyetik alan
çalışmasında kullanışlıdır.
Vektörel Gösterim
Vektörel Gösterim
Vektörel gösterim
Skaler gösterimi
Vektörel çarpımın üç adet skaler eşleniğine göre vektörel eşitliği daha
iyi ifade ettiği görülmektedir.
Vektörlerde Toplama Çıkarma
İki vektörün nokta (skaler) çarpımı
İki vektörün nokta (skaler) çarpımı
Nokta çarpımının bazı temel özellikleri
İki vektörün vektörel çarpımı
Sağ El Kuralı
Vektörel çarpım
Vektörel çarpım
Vektörel çarpım
Vektörel çarpım
Karma çarpım
Karma çarpım
Sorular
Koordinat Sistemleri ve Dönüşümler
Koordinat Sistemleri
• Uzayda bir noktayı göstermek ve vektörleri görselleştirerek daha kolay
anlaşılmasını sağlamak için koordinat sisteminden faydalanılır. Verilen bir
vektör matematiksel olarak seçilen koordinat sistemi üzerinde bileşenlerine
ayrılarak ifade edilir.
• Uzayda çok sayıda dikgen (orthogonal) koordinat sistemi mevcuttur.
Burada dikgen terimi koordinat sistemi içinde her bir noktanın birbirlerine
dik üç yüzeyin kesişimi ile tanımlanabileceğini anlatmaktadır.
• Elektromanyetik teoride alanları ve dalgaları ifade etmek için Kartezyen
(Cartesian), silindirik (cylindrical) ve küresel (spherical) koordinat
sistemlerinden faydalanılır. Verilen bir vektör ifadesi için koordinat
sistemleri arasında dönüşüm yapmak mümkündür.
Koordinat Sistemleri
Kartezyen Koordinat Sistemi
Koordinat eksenlerinin (çizgilerinin)
DOĞRU şeklinde olduğu ortogonal
(dikey) sistemlerdir.
P(x,y,z) noktasını, eksenlere
düşen kenar uzunlukları
belirlemektedir.
Kartezyen Koordinat Sistemi
Kartezyen Koordinat Sistemi
Silindirik Koordinat Sistemi
Silindirik Koordinat Sistemi
Silindirik Koordinat Sistemi
Küresel Koordinat Sistemi
Küre üzerindeki bir nokta bu sistemde üç tane bileşenle ifade edilir, bunlar r, θ ve ф' dir.
Koordinatların tanımlı oldukları aralıklar ve tanımları şu şekilde verilir.
r: Yarıçap P ve (0,0,0) noktası arasındaki uzaklıktır.
θ: Enlem, z-ekseni ve çap arasındaki açıdır.
ф: Boylam, x-ekseni ile çapın xy-düzlemine izdüşümü (ρ) arasındaki açıdır.
Bu sistem, dünya üzerinde
coğrafi
konum belirlerken
kullanılan sistemdir. Dünya' nın
yüzeyi üzerinde her noktada
yarıçap
aynı
olduğundan,
sadece enlem ve boylam ile bir
yer belirlenebilir.
Küresel Koordinat Sistemi
Küresel Koordinat Sistemi
Sorular (1)
Sorular (2)
Sorular (3)
Sorular(4)
Elektrik Yükleri ve Alanlar
• Bu bölümde durgun yüklerden dolayı oluşan statik elektrik
alanları (elektrostatik) işlenecektir.
• Statik elektrik alanları === Yük zamanla sabit
• Coulomb deneyleri sonucu yüklü iki parçacık arasındaki
elektrik kuvvetinin
Yüklerin çarpımı ile doğru orantılı,
Yüklerin aralarındaki uzaklığın karesi ile ters orantılı,
Yüklerin birbirini birleştiren hat boyunca yönlenmiş ve
Aynı yükler için itici ve zıt yükler için çekici
ELEKTRİK ALAN ŞİDDETİ
Eğer bir yük diğerine doğru hareket ettirilirse Coulomb kanununa göre yükler
tarafından etkiyen kuvvetin de ani olarak değişmesi gerekir.
Bunun tersine görecelik teorisi bir yükün hareketi hakkındaki bilginin diğer yüke
ulaşması için belli bir zaman alması gerektiğini zorunlu kılmaktadır.
Bundan dolayı yükler üzerine etkiyen kuvvetlerin artışı ani olamaz böylece yük
sistemleri ile ilgili enerji ve momentin geçici olarak denge dışı olacağı gösterilir.
Cisimlerden kaçan (kaybolan) moment ve enerjinin hesaba katılması için
etkileşen cisimlerin bulunduğu ortamda, alanın biçimini bozucu etki gösteren
ekstra bir şeyin var olması gerekir.
Bu yüzden, bir yük üzerine başka bir yükün varlığında etkiyen kuvvetin bir alan
olarak tanımlanması oldukça kullanışlı olmaktadır.
ELEKTRİK ALAN ŞİDDETİ
Yükü çevreleyen uzayda her yerde bir elektrik alanı veya elektrik alan şiddetinin
var olduğu söylenebilir.
𝑬 uzayda bir noktadaki elektrik alan şiddeti ise bu noktada q yüküne etkiyen
kuvvet:
q nokta yükünden dolayı P noktasındaki elektrik alan şiddetinin ifadesi:
ELEKTRİK ALAN ŞİDDETİ
Elektrik alan çizgileri
• Bir pozitif yükten çıkıp bir negatif yükte son bulurlar
• Bir pozitif yükten ayrılan veya bir negatif yüke ulaşan alan çizgilerinin sayısı
yük miktarıyla orantılıdır.
• Asla birbirlerini kesmezler
İki Levha Arasındaki Elektrik Alan Şiddeti
Elektrik Alan ile Manyetik Alan Arasındaki Farklar
• Manyetik alan hareket eden elektrik yükleri tarafından, zamanla değişen
elektrik alanlardan veya temel parçacıklar tarafından içsel olarak üretilir.
• Zamana göre değişen bir elektrik alan (mesela hareketli bir yüklü
parçacık nedeniyle) yerel manyetik alana sebep olur.
Elektrik Alan ile Manyetik Alan Arasındaki Farklar
• Manyetik alan çizgileri kapalı eğrilerdir. Bir başka deyişle manyetik alan
çizgilerinin başlangıcı ve sonu yoktur. Oysa elektriksel alan çizgileri artı
işaretli yüklerden çıkıp eksi işaretli yüklerde son bulmaktadır.
• Elektrik kuvveti, her zaman elektrik alanına paralel, buna karşın manyetik
kuvvet manyetik alana dik olarak etkir.
Örnek: 24 μC yük değerine sahip bir cisim düzgün 610 N/C elektrik alanın
içerisinde havada asılı durmaktadır. Cismin kütlesini hesaplayınız.
Elektriksel Akı ve Gauss Yasası
Elektriksel Akı
• Statik Elektrik, tabiatta birbirinden farklı veya aynı, iletken veya yalıtkan
iki maddenin temas etmesi ve sonra ayrılması veya sürtünme işlemi
sonucunda, bu iki cisim arasında pozitif ve negatif elektronların serbest
bırakılması ve işaretlerinin değişmesi sonucunda oluşur. Statik yükün
voltajı çok fazla olmasına karşın, akımı çok zayıftır.
• Maddeler birbirleriyle temas halinde olduğu sürece aralarında temas yüzeyi
boyunca elektron transferi olur. İki maddenin temasının kesilmesi
durumunda aralarındaki sınır tabakası ortadan kalkar ve maddelerden
birinde negatif yük fazlalığı (negatif yüklenme) diğerinde ise elektron
azlığı (pozitif yüklenme) meydana gelir. Oluşan bu iki ayrı yük birbirlerini
çeker ve arada bulunan hava gibi yalıtkan olan bir ortam boyunca ark
(kıvılcım) yaparak boşalır ve yük farklarını dengelerler.
Elektriksel Akı
• Yük veya yükler kapalı bir hacim içerisine alındıklarında, bu
kapalı alandan dışarı veya içeri doğru elektrik alan çizgileri
düşünülebilir.
Elektriksel Akı
Alan çizgileri birbirine yakın olduğunda E büyük, uzak olduğunda küçüktür.
Alan çizgileri bir artı yükten çıkıp bir eksi yükte son bulmalıdır.
Alan çizgilerinin sayısı yük miktarıyla orantılıdır.
İki alan çizgisi birbirini kesmez.
Elektriksel Akı
Elektrik akısı, bir yüzeyden geçen elektrik alan çizgilerinin sayısıyla doğru
orantılıdır.
Çok küçük bir dA alanındaki elektrik akısı şu şekilde hesaplanır:
Burada E yüzeye dik olan elektrik alanıdır. Bir S yüzeyinden geçen elektrik akısı dA
alanlarının toplanmasıyla elde edilir:
Elektrik alanı vektörüyle, dA vektörü arasında skaler çarpım olduğundan manyetik
akının büyüklüğü şu şekilde yazılır:
Elektriksel Akı
Elektriksel Akı- Soru
Gauss Kanunu
Noktasal Yükte Gauss Kanunu
Küresel Yükte Elektrik Alanı
Yük Dağılımları
Noktasal, çizgisel, alana yayılan (düzlemsel), hacim içerisine yayılan yükler
Gauss Yasası Kullanılarak Hesaplanan Bazı Örneksel Elektrik Alanları
Sorular (1)
Sorular (2)
Sorular (3)
Sorular (4)
Sorular (5)
Diverjansın Fiziksel Anlamı ve Uygulamaları
Diverjans Nedir
• Isındıkça genişleyen havanın hızını gösteren bir vektör alanının
uzaksaması pozitif olacaktır, çünkü hava genişlemektedir. Eğer
hava soğuyup daralıyorsa uzaksama negatif olacaktır. Bu
örnekte uzaksama yoğunluğun değişiminin ölçüsü olarak
düşünülebilir.
• Vektör hesaplamada, diverjans (ıraksama, uzaksama,
uzaklaşma) bir vektör alanının kaynak ya da batma noktasından
uzaktaki bir noktada genliğini ölçen işleçtir; yani bir vektör
alanının uzaksaması işaretli (artı ya da eksi) bir sayıdır.
• Uzaksaması her yerde 0 olan vektör alanına selenoidal denir.
Diverjans Nedir
Soru (1)
Soru (2)
Hatırlatma
Hatırlatma
Hacmin Türevi
Alan
Alanın Türevi
Vektör
Vektörün Türevi
Nokta
Diverjans bulurken bir vektör alanının kısmi
türevini alarak vektör buluyoruz
Diverjans İşareti
Selenoidal Diverjans
Diverjans Uygulamaları-1
Diverjans Uygulamaları-2
Diverjans Uygulamaları-3
Diverjans Uygulamaları-4
6-Statik Elektriksel Alanın Endüstriyel
Uygulamaları
Yüklü Parçacığın Sapması
• Elektrostatik alanların en yaygın uygulamalarından biri elektron veya
proton gibi yüklü bir parçacığın yörüngesinin kontrol edilmesi için
saptırılmasıdır.
• Katot ışınlı osiloskop, mürekkepli-jet yazıcı ve hız seçici gibi aygıtlar bu
prensibe dayanmaktadır.
• Yüklü parçacığın sapması bir çift paralel plaka arasındaki potansiyel fark
korunarak yapılır.
• ux hızı ile x yönünde hareket eden m kütleli ve q yükü ile yüklü bir
parçacığı dikkate alalım. t=0 zamanında yüklü parçacık Vo potansiyel
farkında tutulan paralel levha çifti arasındaki bölgeye girer.
Yüklü Parçacığın Sapması
Hız=İlk hız + ivme ∙ zaman
V = V0 + a ∙ t
Yüklü Parçacığın Sapması
Yüklü Parçacığın Sapması- Örnek
KATOT IŞINLI OSİLOSKOP
Katot ışınlı osiloskop’un temel özellikleri; tüp camdan yapılmış ve içi tamamen
boşaltılmıştır. Isıtıcı bir flaman ile ısıtıldığında katot elektron yayar. Bu
elektronlar daha sonra katota göre birkaç yüz voltluk bir potansiyelde tutulan
anoda doğru hızlandırılır. Küçük bir deliğe sahip olan anot, içinden ince bir
elektron ışınının geçmesine izin verir. Hızlanmış elektronlar bundan önceki
kısımda tartışılana benzer bir davranışla hem yatay ve hem de dikey
boyutlarda saptırılabilecekleri bir bölgeye girerler. Son olarak elektron ışını bir
cisim (fosfor) ile kaplanmış görünür ışık yayan ekranın iç yüzeyine
bombardıman edilir.
KATOT IŞINLI OSİLOSKOP
KATOT IŞINLI OSİLOSKOP
KATOT IŞINLI OSİLOSKOP
KATOT IŞINLI OSİLOSKOP
MÜREKKEPLİ YAZICI
MÜREKKEPLİ YAZICI
MİNERALLERİN AYRIŞTIRILMASI
MİNERALLERİN AYRIŞTIRILMASI
MİNERALLERİN AYRIŞTIRILMASI
MİNERALLERİN AYRIŞTIRILMASI
7- Elektrik Potansiyeli
Elektrik Potansiyeli
Elektrik Potansiyeli
Elektrik Potansiyeli
Elektrik Potansiyeli
Elektrik Alanda Yapılan İş
Elektrik Alanda Yapılan İş
Nokta Yükün Elektrik Potansiyeli
Soru-1
Soru-2
Soru-3
Soru-4
Soru-4
Soru-5
Soru-6
Soru-7
Soru-8
Soru-8
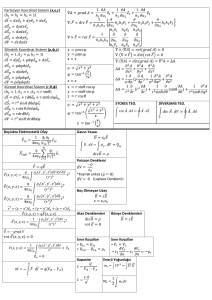
Hatırlatma---- Sınavda verilecek formül ve değerler
8-Enerji
Enerji
Enerji
Enerji
Soru-1
Soru-2
Soru-3
Soru-4
Enerji
Enerji
Enerji
Enerji
Enerji
Enerji
Enerji
Enerji
Enerji
Enerji
Enerji
9- Akım ve Akım Yoğunluğu
Akım ve Akım Yoğunluğu
İletkenlik
Direnç
Akım Tabakası Yoğunluğu
Soru-1
Soru-2
Soru-3
Soru-4
Soru-5
Sorular
10-İletkenler, Yalıtkanlar ve Sınır
Şartları
İletkenler ve Sınır Şartları
İletkenler ve Sınır Şartları
İletkenler ve Sınır Şartları
İletkenler ve Sınır Şartları
İletkenler ve Sınır Şartları
İletkenler ve Sınır Şartları
İletkenler ve Sınır Şartları
Soru-1
Soru-1
Soru-2
Soru-2
Kutuplanma (P) ve Bağıl Geçirgenlik (εr)
Kutuplanma (P) ve Bağıl Geçirgenlik (εr)
Kutuplanma (P) ve Bağıl Geçirgenlik (εr)
Kutuplanma (P) ve Bağıl Geçirgenlik (εr)
Dielektriğin Ayırma Yüzeyinde Sınır Koşulları
Dielektriğin Ayırma Yüzeyinde Sınır Koşulları
11- Kapasitör ve Uygulamaları
Kapasitör ve Uygulamaları
Kapasitör ve Uygulamaları
Kapasitör ve Uygulamaları
Çok Katmanlı Dielektrikli Kondansatörler
Çok Katmanlı Dielektrikli Kondansatörler
Çok Katmanlı Dielektrikli Kondansatörler
Kondansatörlerde Biriken Enerji
Sabit Gerilim Durumunda D ve E
Sabit Gerilim Durumunda D ve E
Soru-1
Soru-1
Soru-2
Sorular
12-Laplace ve Poisson
Denklemlerinin Çözüm Tahminleri
Laplace ve Poisson Denklemleri
Laplace ve Poisson Denklemleri
Soru-1
Soru-2
Soru-3
Soru-5
Eş merkezli tam dairesel iki silindir arasındaki bölgede, r = 1 mm'de V = 0 ve r = 20 mm'de
V = 150 V olmak üzere, potansiyel fonksiyonunu ve elektrik alan şiddetini bulunuz.
Soru-5
Soru-6
Soru-7
Soru-8
Soru-9