MADDEDicle VE ELEKTRİKS

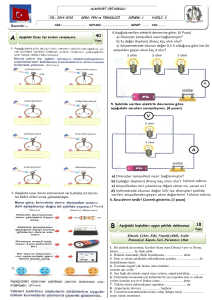
MADDE VE ELEKTRİK
Elektriklenme ve Elektrik Yükü
Elektrik yükünü ileten maddelere iletken maddeler , iletmeyen maddelere de yalıtkan maddeler
Maddeler üç şekilde elektriklenirler.
1- Sürtünme ile elektriklenme
2- Dokunma ile elektriklenme
3- Etki ile elektriklenme
denir.
1- Sürtünme İle Elektriklenme
Bir cam çubuğu bir ipek parçasına sürtüp yalıtkan bir iple asalım. İkinci bir cam çubuğu yine ipek parçasına
sürtüp birinci cam çubuğa yaklaştırırsak birbirini iter.
Benzer şekilde bir ebonit çubuğu yünlü kumaş parçasına sürtüp yalıtkan bir iple asalım. İkinci bir ebonit
çubuğu yine yünlü kumaş parçasına sürtüp birinci ebonit çubuğa yaklaştırırsak yine birbirini iter.
Bir cam çubuğu ipek parçasına sürtüp yalıtkan bir ip ile asalım. Bir ebonit çubuğu yünlü kumaş parçasına
sürtüp çam çubuğa yaklaştırırsak birbirini çeker.
Buradan şu sonuçlar çıkarılabilir : Maddeler sürtünme ile elektriklenebilirler. İki çeşit elektrik yükü vardır.
Cam çubuk ve onun yükü gibi yüklere Pozitif ( + ) yük denir. Ebonit çubuk ve onun yükü gibi yüklere de
Negatif ( - ) yük denir. Aynı yükler birbirini iter , farklı yükler birbirini çeker. Sürtünmede sürtünen
maddelerden biri (+) yükle yüklenirse diğeri ( - ) yük ile yüklenir. Örneğin cam çubuk ipek parçasına
sürtündüğünde cam çubuk (+) yük ile yüklenirken ipek parçası (-) yük ile yüklenir.
Durgun haldeki elektrik yüklerine Statik ( Durgun ) elektrik denir. Durgun halde bulunan elektrik yükleri
arasındaki kuvveti ve bununla ilgili kavramları inceleyen FİZİK dalına Elektrostatik denir.
Nötr :Pozitif ve negatif yüklerin birbirine eşit olmasıdır.
Topraklama : Yüklü cisimlerin , iletken tel ile toprağa bağlanmasına topraklama denir.
Topraklama ile yükler toprağa veya yer küreye geçer. Yer küre elektrikçe nötr kabul edilir.
Topraklama bu şekilde gösterilir.
Elektroskop :
Bir cismin elektrik ile yüklü olup olmadığını yüklü ise hangi tür elektrik yükü ile
yüklü olduğunu anlamamıza yarayan araçtır.
Elektroskopun her iki yaprağı aynı yük ile yüklenir.
2- Dokunma İle Elektriklenme
Yüklü bir cismi yüksüz elektroskopa dokundurursak elektroskopun yaprakları açılır. Yapraklarının
açılmasının nedeni yüklü cisimden bir miktar yükün elektroskopa geçmesidir.
Yüklü bir cisim yüksüz bir cisme dokundurulduğunda onu da aynı cins elektrik yükü ile yükler. Buna
dokunma ile elektriklenme denir.
NOT: Maddeler elektrik yüklerini dış yüzeylerine veya sivri uçlarına geçirirler. iç yüzeyleri ise yüksüzdür.
Birbirine dokunan cisimlerin elektrik yükleri bu cisimler tarafından paylaşılır. Yüklerin paylaşımı cisimlerin
fiziksel özelliklerine bağlı olarak değişir. Küre şeklindeki cisimler birbirine dokundurulduğunda yükler kürelerin
yarıçapları ile orantılı olarak paylaşılır. Levha şeklindekiler ise alanları ile orantılı olarak paylaşılır. Yük q ile
gösterilir. Yük birimi C (Coulomb = Kulon) dur.
1
Yükü qA ve yarı çapı rA olan küre şeklindeki iletken A cismi ile yükü q B ve
yarı çapı rB olan küre şeklindeki iletken B cismi birbirine dokundurulduğunda son
yükleri şu formül ile bulunur :
qA' = ( qA + qB ). rA
qB' = ( qA + qB ). rB
rA + rB
rA + rB
Örnek :
A ve B iletken kürelerinin birbirine değdirilip ayrıldıktan sonraki yüklerini
bulun.
Çözüm : qA(son) = ( qA + qB ). rA = ( 10q + 2q ) . 3r = 12q . 3r = 9q
rA + rB
3r + r
4r
qB(son) = ( qA + qB ). rB = ( 10q + 2q ) . r = 12q . r = 3q
rA + rB
3r + r
4r
Örnek :
A küresi önce B küresine değdirilip ayrıldıktan sonra C küresine
değdirilip ayrılırsa A küresinin en son yükü ne olur.
Çözüm :
qA' = ( qA + qB ) . rA = ( 7q + 3q ) . 3r = 10q . 3r = 6q
rA + rB
3r + 2r
5r
qA"= ( qA ' + qC ) . rA = ( 6q – 2q ) . 3r = 4q . 3r = 3q
rA + rC
3r + r
4r
3- Etki (Tesir ) ile Elektriklenme
Yüklü bir cisim yüksüz elektroskopun topuzuna yaklaştırılırsa yapraklar açılır. Yüklü cisim uzaklaştırılınca
yapraklar kapanır. Böylece yüksüz bir cisim yüklü bir cismin etkisi ile yüklenebilir. Buna etki ile elektriklenme
denir.
NOT : Yüksüz bir elektroskopa yüklü bir cismi yaklaştırırsak
yapraklar cismin yükü ile aynı işaretli olarak yüklenir.
Elektroskopun topuzu ise cismin yükünün ters işaretlisi yük ile
yüklenir.
NOT : Yüklü bir elektroskopa aynı
işaret ile yüklü bir cismi yaklaştırırsak
yapraklar daha da açılır. ( Şekil a )
Yüklü bir elektroskopa ters işaret
ile yüklü bir cismi yaklaştırırsak
yapraklar biraz kapanır. ( Şekil b )
Etki ile elektriklenen yüksüz bir cismin , yüklü
çubuğa yakın olan kısmı çubuk ile farklı cins elektrik
yükü ile yüklenir. Uzak olan kısmı da çubuk ile aynı
tür elektrik yükü ile yüklenir.
Etki ile elektriklenmede cisimler arasında yük alış verişi olmaz. Sadece cisim üzerindeki yükler ayrılır.
Yüksüz iki iletken metal çubuk birbirine değecek şekilde yalıtkan
iki cam bardak üzerine bırakılıyor. Metal çubuklara ( + ) yüklü bir
cisim yaklaştırılırsa yüklü cisme yakın olan metal çubuk (- ) yüklü
olur. Diğer taraftaki metal çubuk ise ( + ) yüklü olur. (+) yüklü
cisim kaldırılmadan cam bardaklar ile birlikte metal çubukları
2
birbirinden ayırırsak yükler geri gidemez ve yakın olan metal çubuk ( - ) yüklü kalır. Diğeri de ( +) yüklü kalır.
Yüksüz bir metal üzerindeki elektrik yüklerinin metale yaklaştırılan yüklü cismin etkisi ile ayrılması olayına
etki ( tesir ) ile elektriklenme veya elektrostatik indüksiyon denir. Ayrılan bu yüklere de indüksiyon yükleri
denir.
Örnek1 :
Birbirine değmekte olan A , B , C iletkenlerinin sağ
ve sol tarafına eşit değerde (+) yük bırakılıyor. A , B ,
C ‘ nin yüklerinin miktarı ve türünü bulun.
Çözüm : Sol taraftaki yük (-) yükleri kendine doğru yani A ya çeker ve (+) yükleri iter. sağ taraftaki yük de (-)
yükleri kendine doğru çeker yani C ye çeker ve (+) yükleri iter. Dolayısıyla (+) yükler B ye sıkışır. Sol taraftaki
yük +q kadar yükü A ya çekerse +q kadar yükü de B ye iter. Benzer şekilde sağ taraftaki yük de -q kadar
yükü C ye çekerse +q kadar yükü B ye iter. A = -q
B = +2q
C = -q
olur.
Örnek2 :
Yüksüz silindirin içine (+) yüklü A küresi şekildeki gibi iç tarafa değmeden
sarkıtılıyor. Silindirin iç ve dış yüzeylerinin yüklerinin cinsi ne olur.
Çözüm :
(+) yüklü A küresi Nötr olan silindirdeki (-) yükleri iç tarafa doğru çeker ve (+)
yükleri dış yüzeye doğru iter.
iç = -
Dış = +
olur.
Örnek3 :
Yüksüz silindirin içine (+) yüklü A küresi içten değecek şekilde bırakılıyor.
Silindirin iç ve dış yüzeyi ile A küresinin yük bakımından durumu ne olur.
Çözüm :
Maddeler elektrik yüklerini dış yüzeylerine verirler. iç yüzeyleri ise yüksüzdür.
(+) yüklü A küresi silindirin iç tarafına değince yüklerini silindirin iç tarafına
verir. Silindir de bu yükleri dış tarafına iletir. Dolayısıyla silindirin iç tarafı ve A
küresi yüksüz olur ve Silindirin dış tarafı (+) yüklü olur.
iç = yüksüz
Dış =+
A küresi = yüksüz
3
Örnek4 :
(+) yüklü A küresi yüksüz silindirin dış tarafına değecek şekilde bırakılıyor.
Silindirin iç ve dış yüzeyi ile A küresinin yükü ne olur.
Çözüm :
(+) yüklü A küresi yüksüz silindire dıştan değdiği için yüklerinin bir
kısmını silindire verir. Silindir bu yükleri dış yüzeyine dağıtır. Silindiri iç tarafı
yüksüz kalır.
A küresi = + yüklü
Dış taraf = + yüklü
iç taraf = Nötr
Örnek5 :
Yalıtkan iplikler ile asılı A küresi B küresini itip C küresini çekiyor. C küresi
(+) yüklü olduğuna göre A ve B kürelerinin yüklerinin cinsi ne olur.
Çözüm :
A küresi C küresini çektiği için (-) yüklüdür.
B küresi A tarafından itildiği için (-) yüklüdür.
Örnek6 :
Yüklü M çubuğu yüklü X ve Y elektroskoplarına değmeden
yaklaştırıldığında X in yaprakları biraz açılıyor Y nin yaprakları
biraz kapanıyor. X ; Y ve M nin yüklerinin işareti için ne
söylenebilir.
Çözüm :
M çubuğu yaklaştırıldığında X in yaprakları biraz açıldığı için X ve M aynı işaretlidir.
M çubuğu yaklaştırıldığında Y nin yaprakları biraz kapandığı için Y ve M farklı işaretlidir.
Örnek7 :
B ucu toprağa bağlı iletken cisme şekildeki gibi (+) yüklü cisim
yaklaştırılırsa A ve B uçlarının yük durumu ne olur.
Çözüm :
A ucu (-) olur. B ucu ise topraktan negatif yükleri alarak nötr
olur.
Örnek8 :
Şekilde özdeş elektroskoplardan E1
elektroskopu silindirin dış tarafına , E2
elektroskopu ise iç tarafına bağlanmıştır. (+)
yüklü A küresi silindirin içine değmeden
sarkıtılınca her iki elektroskopun yaprakları
açılıyor. İletken A küresi içten silindirin
dibine
değdirilirse
bu
durumda
elektroskopların yapraklarının durumu önceki
duruma göre ne olur.
4
Çözüm :
Birinci durumda yani A küresi değmeden
bırakıldığında şekil-1 deki gibi iç taraf (-) dış taraf
artı olur.
Dışa bağlı E1 elektroskopunun yaprakları açık ve
(+) yüklü olur.
İç tarafa bağlı E2 elektroskopunu yaprakları açık
ve (-) yüklü olur.
İkinci durumda A küresi iç taraftan silindire
değdiği için yükünü silindire silindirde dış
tarafına verir. Dış taraf (+) yüklü olur. A küresi
ve silindirin iç tarafı yüksüz olur.
Bu durumda :
Dış taraf bağlı E1 elektroskopunun yaprakları bu
durumda da (+) yüklü ve açık olur.
İç tarafa bağlı E2 elektroskopunun yaprakları ,
iç taraf yüksüz olduğu için kapanır.
Sonuç: E1=Değişmez
E2=Kapanır.
Yük Kaynağı Olarak Atomlar
Bir atom çekirdek ve çekirdeğin etrafında dönen elektronlardan oluşur. Çekirdekte pozitif (+) yüklü protonlar
ve yüksüz nötronlar vardır. Atom kütlesinin hemen hemen tamamı çekirdektir. Elektronların kütlesi çekirdeğin
kütlesine göre çok küçüktür. Nötr atomda proton sayısı ile elektron sayısı birbirine eşittir. Katı maddelerde
hareket eden yükler negatif yüklü elektronlardır. Bir madde dışardan elektron alırsa negatif(-) yükle yüklenir
dışarıya elektron verirse pozitif(+) yükle yüklenir.
Yük Miktarı , Elemanter Yük ve Yükün Parçacıklı Yapısı
Bir atomun yüksüz (Nötr ) olması o atomda hiç yük olmadığı anlamına gelmez. Pozitif (+) ve Negatif (-)
yüklerinin birbirine eşit olması demektir.
Elemanter Yük (e.y) : Bir elektronun yüküne elemanter yük denir. 1e.y veya 1 ē = 1,6 . 10-19 C dir.
Bir elektronun yükü birim yük olarak kabul edilir. Bir elektron ve bir protonun elektrik yükleri değerce
birbirine eşit fakat zıt işaretlidir.
İletken , Yalıtkan ve Yarı İletken Maddeler
Elektrik yükünü ileten maddelere iletken denir. Elektrik yükünü iletmeyen maddelere yalıtkan denir.
Metallerdeki atomların dış yörüngelerinde bulunan elektronlar yörüngelerinden kolayca ayrılabilirler. Hareket
edebilen bu elektronlara serbest elektronlar denir.
İletkenliği oldukça zayıf olan veya elektriği bir yönde iletirken diğer yönde iletmeyen maddelere yarı iletken
denir. Örneğin Si(silisyum) , Ge (germanyum) ve C (karbon) gibi
Vektör : Bir başlangıç noktası , yönü , doğrultusu ve şiddeti (büyüklüğü) olan büyüklüklerdir.
bir vektör şekildeki gibi gösterilir.
İki Vektörün Toplamı
Vektörleri üçgen , paralel kenar ve çokgen kuralı ile toplayabiliriz.
5
1-Üçgen Kuralı İle Toplama :
Üçgen kuralı ile toplamada birinci
vektörün uç kısmına ikinci vektörün
başlangıç noktası getirilir. Daha sonra
birincinin başlangıcından ikincinin bitişine
yani uç kısmına bir vektör çizilir. Bu
vektör toplam vektörüdür.
2-Paralel Kenar Kuralı ile Toplama :
Paralel kenar kuralı ile toplamada
her iki vektörün başlangıç noktaları
birleştirilir.
Sonra
her
ikisinin
uçlarından paralel çizgiler çizilir. Daha
sonra başlangıç noktalarında bu
çizgilerin kesiştiği noktaya bir vektör
çizilir . Buda toplam vektörü verir.
Ters Vektör : Doğrultusu ve şiddeti aynı , fakat yönü 180o ters olan vektördür.
Aynı Doğrultulu Aynı Yönlü İki Vektörün Toplamı :
Çözüm :
Burada iki vektör arasındaki açı α = 0o dır. Bileşke vektörün büyüklüğü
her iki vektör toplanarak bulunur. Yönü vektörlerle aynı yöndedir.
Örnek : Aynı doğrultulu aynı yönlü iki vektörden a=20 birim
b=15
birim ise bileşke vektör ne kadardır.
c=a + b = 20 + 15 = 35 birim.
Aynı Doğrultulu Zıt Yönlü İki Vektörün Toplamı :
Burada iki vektör arasında α =180o açı vardır. Bileşke vektör büyük olan
vektörden küçük vektör çıkarılarak bulunur. Bileşke vektörün yönü büyük
vektör ile aynı yöndedir.
Örnek : Aynı doğrultulu fakat zıt yönlü iki vektörden a=20 birim b=15
birimdir. Bileşke vektörü ve yönünü bulun.
Çözüm : c = a + (-b) = a - b = 20 – 15 = 5 birim.
Kesişen İki Vektörün Toplamı :
Kesişen iki vektör arasındaki açı α
şu formül ile bulunur :
ise bu iki vektörün bileşkesi
c2 = a2 + b2 + 2 .a .b . Cos α
Eğer α =90o ise c2 = a2 + b2 olur.
6
Örnek : 6N ve 8N luk iki kuvvet arasındaki açı
a) α =60o
b) α =90o olursa bileşke kuvvet ne kadar olur. (Cos 60=0,5
Cos 90 =0 )
Çözüm :
a) c2 = a2 + b2 + 2 .a .b . Cos α = 62 + 82 + 2. 6. 8. Cos 60 = 36 + 64 + 96 . 0,5 = 148
b) c2 = a2 + b2 = 62 + 82 = 36 + 64 = 100 ise c = 10 N olur.
ise c = 12 , 16 N
Yüklü Cisimler Arasındaki Etkileşme Kuvvetleri
Elektrik yüklerinden kaynaklanan kuvvetlere elektriksel kuvvetler denir.
a) Kuvvetin Yük Miktarına Bağlılığı : İki yük arasındaki elektriksel kuvvet diğer adıyla itme veya çekme
kuvveti yüklerin birbirine çarpımıyla doğru orantılıdır.
F α q1 . q2 dir.
b) Kuvvetin Uzaklığa Bağlılığı : Elektriksel kuvvet yüklerin arsındaki uzaklığın karesiyle ters orantılıdır.
F α 1 / d2 dir.
c) Kuvvetin Ortama Bağlılığı : ( Ortamın Elektriksel Geçirgenliği ) : Elektriksel kuvvet bu yükler arasındaki
ortama göre değişir.
Fα k
( k= Coulomb sabiti )
εo = 1 /4πk = 8,85.10-12 C2 / n.m2
k = 9.109 N.m / C2 dir.
d) Kuvvet , Yük Uzaklık ve Ortam Arasındaki Bağıntı :
Coulomb Kanunu : İki elektriksel yük arasındaki itme veya çekme kuvveti bu iki yükün birbirine çarpımıyla
doğru orantılı aralarındaki uzaklığın karesiyle ters orantılıdır.
F = k . q1 . q2
d2
Burada F kuvvet , q1 ve q2 yükler d yükler arasındaki uzaklıktır , k coulomb sabitidir.
ÖRNEKLER
Örnek1 : Birbirinden 2 metre uzaklıkta bulunan q1 = 4. 10-3 C ve q2 = 6. 10-3 C yükleri arasındaki itme
kuvvetini bulun. ( k=9. 109 Nm2 /C2 )
Çözüm :
F = k. q1 . q2 = 9. 109 . 4. 10-3. 6. 10-3 =54 . 103 N
d2
22
Örnek2 : İki özdeş yüklü cismin birbirlerine x kadar uzaktan uyguladıkları kuvvet F 1 dir. Cisimlerin yüklerini
iki katına çıkartıp aradaki uzaklığı üçte birine indirirsek bu durumdaki F 2 etkileşme kuvveti kaç F1 olur.
Çözüm : q1 = q2 = q olsun
F1 = k.q1 . q2 = k.q.q
F2 = k. q1 . q2 = k. 2q . 2q = 4 . k. q.q = 36 .k.q.q
d2
x2
d2
( x / 3 )2
x2 / 9
x2
k.q.q
F1 =
x2 = 1
F1 / F2 = 1 /36 ise F2 = 36 . F1
F2 36.k.q.q
36
x2
Örnek3 :
A , B ve C küreleri aynı doğru üzerindedir.
a) A küresine etki eden bileşke kuvveti
bulun?
b) B küresine etki eden bileşke kuvveti
bulun? ( k=9.109 )
Çözüm :
a)
FAB = k.qA . qB = 9.109. 4.10-3.2.10-3 = 72.109.10-6 =72.103 =18.103.104 = 18.107 N
(AB)2
(0,02)2
0,0004
4.10-4
FAC = k.qA . qB = 9.109. 4.10-3.8.10-3 = 288.109.10-6 = 8.107 N
(AC)2
(0,06)2
36.10-4
Burada her iki kuvvette aynı yönlü olduğundan
FA = FAB + FAC = 18.107 + 8.107 = 26.107 N
7
b)
FBA = - FAB = -18.107
FBC = k.q1 .q2 = 9.109. 2.10-3.8.10-3 = 144.109.10-6 =9.107 N
(BC)2
(0,04)2
16.10-4
Burada kuvvetler aynı doğrultulu zıt yönlü olduğundan bileşke kuvvet
FB = FBA – FBC = 18.107 – 9.107 = 9.107 N olur.
Örnek4 :
A küresi ile C küresi arasındaki uzaklık 10
metredir. A ile C arasında A’dan ne kadar
uzakta B yüküne etki eden bileşke kuvvet sıfır
olur.
Çözüm : Bileşke kuvvet sıfır ise ,burada aynı doğrultulu zıt yönlü olan F BA
ile FBC birbirine değerce eşittir.
Burada AB uzaklığı x ise BC uzaklığı 10 – x olur.
FBA = FBC
k.qA .qB = k.qB . qC
qA = qC
9 = 4
karekök alınırsa
x2
(10 - x )2
x2
(10 – x )2
x2
(10 – x )2
3 = 2
olur.
2x = 3(10 – x )
2x = 30 – 3x ten 5x = 30 x = 6 metre bulunur.
x 10 - x
Örnek5 : Yarıçapları eşit yükleri qA = 2q ve qB = 10q olan A ve B kürelerinin birbirlerine x kadar
uzaktan uyguladıkları kuvvet F 1 dir. Bu yükleri birbirine değdirip sonra 2x uzaklığına bıraktığımızda
birbirine uyguladıkları kuvvet F2 oluyor. F1 / F2 oranını bulun.
Çözüm :
F1 = k.qA .qB = k. 2q.10q = 20 k.q2
d2
x2
x2
qA' = ( qA + qB ).rA = (2q + 10q ). r = 6q
rA = rB olduğundan
rA + rB
2r
F2 = k. qA' . qB' = k.6q . 6q = 36 k.q2 = 9k.q2
d2
(2x)2
4x2
x2
F1
F2
= 20k.q2 / x2 = 20 / 9
9k.q2 / x2
qB' = 6q olur.
olur.
Örnek6 : Yarı çapı 3r yükü qA = 6q olan bir A küresi ile yarı çapı r yükü q B = 10q olan B küresi x
uzaklıktan birbirine uyguladıkları kuvvet
F1
dir. Bu iki yükü birbirine değdirip aynı uzaklığa
bıraktığımızda bu defa birbirine uyguladıkları kuvvet F2 oluyor. F1 / F2 oranını bulun.
Çözüm :
F1 = k.qA .qB = k. 6q.10q = 60 k.q2
d2
x2
x2
qA' = ( qA + qB ).rA = (6q + 10q ). 3r = 12q
rA + rB
3r + r
qB' = ( qA + qB ).rB = (6q + 10q ). r = 4q
rA + rB
3r + r
F2 = k. qA' . qB' = k.12q . 4q = 48 k.q2
d2
x2
x2
F1
F2
= 60k.q2 / x2 = 60 / 48 = 5 / 4
48k.q2 / x2
olur.
8
Örnek7 : Birbirinden 3 metre uzakta bulunan iki yük arasındaki kuvvet 6.105 Newton dur. Yüklerden biri
2.10-2 C ise ikinci yük ne kadardır. ( k = 9.109 )
Çözüm :
F = k. q1 . q2
6.105 = 9. 109 .2. 10-2. q2
2
d
32
5
5
-7
-2
q2 = 6.10 = 3.10 . 10 = 3.10 C
olur.
2. 107
Örnek8 :
Şekildeki karede B köşesindeki yüke etki eden bileşke
kuvveti bulun.? (k=9.109 , Cos 90 =0 )
Çözüm:
FBA = k.qB .qA = k.4.6 = 6k
d2
22
FBC = k.qB . qC = k. 4.8 = 8k
d2
22
2
2
2
2
FB = FBA + FBC
FB = (6k)2 + (8k)2 =36k2 + 64k2 =100k2
2 1/2
FB = ( 100k )
FB = 10k = 10.9.109 = 90.109 N
Örnek9 :
Şekildeki üçgende A köşesindeki yüke etki eden
bileşke kuvveti bulun ? ( k= 9.109 , Cos 60=0,5 )
Çözüm :
FAB = k.qA . qB = 9.109. 2.10-3.5.10-3 = 9.109.10-6 =10.103 N
d2
32
9
FAC = k.qA . qC = 9.109. 2.10-3.3.10-3 = 54.109.10-6 = 6.103 N
d2
32
9
FA2 = FAB2 + FAC2 + 2.FAB . FAC . Cos60 = ( 10.103 )2 + ( 6.103 )2
+ 2. 10. 103.6.103 . 0,5
FA2 = 100.106 + 36.106 + 60.106 = 196.106
FA2 = 196.106
ise FA = ( 196.106 )1/2 = 14.103 Newton
9
Örnek10 : Aralarında 5.10-10 metre uzaklık bulunan özdeş iki noktasal yük birbirlerine 3,6.10-8 Newtonluk
kuvvet uyguluyorlar. Bu yüklerin değerini bulun. (k=9.109 )
Çözüm :
F = k.q.q
d2
3,6.10-8 = 9.109 . q2
(5.10-10 )
3,6.10-8 = 9.109 .q2
25.10-20
q2 = 3,6.10-8 . 25.10-20 = 36.10-8.25.10-20 = 4.10-8. 25. 10-20 =100.10-28.10-10 = 10-36
9.109
9.1010
1010
q = ( 10-36 )1/2
q= 10-18 C
Örnek11 :
Şekil-1 de özdeş 4 parçaya
ayrılan karede A noktasındaki
+q yüküne etki eden yükler
görülmektedir. daki yük şekil-2
de hangi tarafa doğru hareket
eder.
Cevap :
3 doğrultusunda hareket
eder.
DİCLE
SELAHATTİN AKÇAY’ a teşekkür ederiz.
10