MALZEME BİLİMİ MAL201 Kristal Yapı

MALZEME BİLİMİ MAL201
Kristal Yapı-Doğrultu ve Düzlemlere ait Miller
İndisleri
Metal ve Seramik Yapılar, Polimer Yapıları,
X Işını Difraksiyonu
ŞUBAT 2016
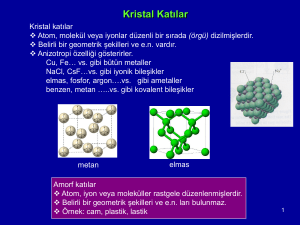
• KRİSTAL YAPILAR
Malzemeler atomların biraraya gelmesiyle
oluşur.
Yapı içinde atomlar, atomlar arası bağ kuvvetleri
ile birarada tutulur.
Yapı içinde atomlar farklı şekillede birarada
bulunabilir:
1.Kristal yapı
2.Amorf yapı
Kristal yapı (uzun mesafede düzenli yapıları (long
range order (LRO) structures)
Burada atomlar üç boyutlu bir düzene göre
dizilirler.
Kristal yapı(Kristal kafes) olarak adlandırılan bu
yapı, metallerde, seramiklerde, cam seramiklerde
ve bazı polimerlerde görülür.
Polimerlerin molekül yapıları karmaşık
olduğundan, bu malzemelerde kristalleşme ancak
yerel ve hacım olarak en fazla %50 oranında
görülür.
Kristal olmayan(Amorf) yapılar
Burada atom veya moleküller rastgele
dizilirler(Örn. Camlar).Bazı malzemelerde örneğin
camlarda olduğu gibi kısa mesafede(örneğin
moleküler mertebede) bir düzen mevcut olabilir.
Kristallerde birim hücre
Üç boyutlu düzende sürekli olarak tekrar eden
yapıya “birim hücre” adı verilir.
Birim hücre kristal içinde tekrar eden yapıların en
basitidir.
Birim hücrelerin kenar
uzunluklarına ve
kenarlar arasındaki
açılara
“kafes parametreleri”
adı verilir.
•
Kristal kafes (lattice): Birim
hücrelerin üç boyutta tekrarı ile
meydana gelen düzendir.
En genel haldeki birim hücre
Birim hücre tanımı
Sürekli tekrar eden yapılar
En basiti
Birim hücre
Kafes sistemleri
Doğadaki bütün kristal malzemeler 7 farklı kristal sisteminden birisine
uyarlar.
Bütün 3D hacmi dolduran kafes
sistemi sadece 7 adet kafes
sisteminden biri olabilir.
1. Kübik
2. Tetragonal
(kare prizma)
3. Ortorombik
(dikdörtgen prizma)
4. Rhomohedral
5. Hegzagonal
6. Monoklinik
7. Triklinik
Bravis Kafes sistemleri
Atomların bu kafes sistemi içerisinde nasıl yerleştiklerini
14 adet “Bravis kafes sistemi” ifade eder.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
Basit Kübik
Hacim Merkezli Kübik
Yüzey Merkezli Kübik
Basit Tetragonal
Hacim Merkezli Tetragonal
Basit Ortorombik
Hacim Merkezli Ortorombik
Taban Merkezli Ortorombik
Yüzey Merkezli Ortorombik
Basit Rombohedral
Basit Hegzagonal
Basit Monoklinik
Taban Merkezli Monoklinik
Triklinik
• Atomlar her bir birim
hücrede kafes noktalarında
bulunur.
• Her bir birim kafes; kafes
kenar ve eksenler arası
açılarını içeren kafes
parametreleri ile ifade edilir.
Şekil 3.2: Birim hücre geometrisi
Aşağıdaki 5 farklı hücrenin 2 boyuttaki gösterimi şekilde
verilmektedir.
•Basit kare
•Basit dikdörtgen
•Alan merkezli dikdörtgen (rhombus)
•Paralel kenar
•Alan merkezli altıgen
Hacim Merkezli Kübik (HMK) Yapı
Figure 3.4 Hacim merkezli yapıkübik (a) Kafes noktaları;
(b)atomların gerçekteki istifi, (c) bir çok kafesin 3 boyutta
istifi.
a
R
a= 4R/√3
ADF = [(Atom sayısı/hücre).(Bir atomun hacmı)]
/ (Birim hücrenin hacmı)
ADF = 2x(4πR3/3)/a3
= 2x(4πR3/3)/(4R/√3)3
= 0,68
•Köşelerde ve merkezde birer atom bulunmaktadır.
•Bu yapıdaki metallerden bazıları; Fe (α-ferrit), V, Cr, Mo, W.
Birim kafesin %68 ‘i atomla
doludur, % 32’si boştur.
Yüzey Merkezli Kübik (YMK) Yapı
•Köşelerde ve yüzey merkezlerinde birer atom bulunmaktadır.
•Bu yapıda metallerin bazıları; Fe (-ostenit), Al, Cu, Ni, vs.
a
R
2R
R
a= 4R/√2
ADF = 4x(4πR3/3)/a3 = 0,74
Hacmin % 74’ü dolu, % 26’sı boştur.
En yüksek doluluk oranı.
3.4 Yüzey merkezli kübik yapı (a) Kafes
noktaları; (b) atomların gerçekteki istifi, (c) bir
çok kafesin 3 boyutta istifi.
Sıkı Düzen Hekzagonal (SDH) Yapı
-Köşelerde : 4x(1/12) = 1/3 ve 4x(1/6)= 2/3
Merkezde . 1 atom olmak üzere ,
birim hücrede toplam 2 atom bulunur.
-Sıkı düzen hegzagonal kafeste ADF= 0,74 tür.
-Bu değer YMK ile aynıdır.
-YMK de en yoğun düzlem (111), SDH de ise (0002) dir.
DOĞRULTU
ve
DÜZLEMLERE
ait
MİLLER İNDİSLERİ
Miller indisleri
Kristal yapıdaki değişik nokta, doğrultu ve düzlemleri
adlandırmak için kullanılır.
-Kafes noktaları
Eksen takımının başlangıcı olarak herhangi bir atom
alınabilir.Kafes noktalarının konumları, birim hücrenin kenar
uzunlukları bir birim kabul edilerek bunların katları veya
kesirleri şeklinde verilir.
Kafes noktalarının gösterilmesi
Kafes Doğrultuları
Kübik sistemde doğrultu ve düzlemleri Miller
indisleri ile ifade edilir.
Şu şekilde saptanır:
• Birim hücrede başlangıç ve
bitiş koordinatları belirlenir.
• Başlangıç koordinatları, bitiş
koordinatlarından aritmetik
olarak çıkarılır.
• Miller indisleri, kesirli
olamaz, tam sayı olmalıdır.
Gerekirse orantılı olarak en
küçük tam sayıya çevrilir.
• Köşeli parantez içine
virgülsüz olarak konur.
•Paralel doğrultular için aynı
indis kullanılır.
Negatif konumlar sayı üzerinde (-) işareti ile
gösterilir; 1 gibi.
Kafes doğrultularının gösterilmesi
Aynı özellikteki doğrultular, örneğin bir kübün hacım köşegenleri
bir doğrultu ailesi oluşturur.Böyle bir aile farklı bir parantezle ,
<111> şeklinde gösterilir.
Doğrultular için Önemli noktalar
1. Eksen takımının başlangıcı herhangi bir atom seçilebilir.
2. Paralel doğrultuların indisleri aynıdır.
3. Aynı indisli fakat negatif işaretli doğrultular aynı değildir.

100  [100]
4. Bir doğrultunun indislerinin aynı tam sayı ile çarpılarak
bulunan indislere ait doğrultular aynıdır.
100x2  200
5. Birbirlerine paralel olmayan (farklı miller indisli) fakat
atom dizilişleri benzer (kübik sistem) olan doğrultular
“doğrultu ailesi” ni oluşturur.










110  110, [110], [11 0], [11 0], 011, [011], [011], [011], 101, [1 01], [101], [1 01]
Doğrultu A
1. Başlangıç ve bitiş: 1, 0, 0, ve 0, 0, 0
2. 1, 0, 0, -0, 0, 0 = 1, 0, 0
3. Kesir veya büyük tam sayı yok.
4. [100]
Doğrultu B
1. Başlangıç ve bitiş: 1, 1, 1 ve 0, 0, 0
2. 1, 1, 1, -0, 0, 0 = 1, 1, 1
3. Kesir veya büyük tam sayı yok.
4. [111]
Doğrultu C
1. Başlangıç ve bitiş: 0, 0, 1 ve 1/2, 1, 0
2. 0, 0, 1 -1/2, 1, 0 = -1/2, -1, 1
3. 2(-1/2, -1, 1) = -1, -2, 2
4.

[1 2 2]
<110> doğrultu ailesi kaç farklı doğrultuyu ifade eder?
Aynı indisli fakat negatif işaretli doğrultular aynı değildir.

100  [100]
vardır.
Bu nedenle Ailede 2 x 6 = 12 adet üye
Kafes Düzlemleri
•Düzlemin eksen sisteminden geçmesi durumunda en yakın
düzleme paralel olarak kaydırılır.
•Düzlemin koordinat eksenini kestiği noktalar belirlenir.
•Bu değerlerin tersi alınır.
•İndisler tam sayı olamalıdır.
Gerekiyorsa orantılı en küçük
tam sayı ile çarpılır.
•Bulunan sayılar normal
parantezde virgülsüz olarak
ifade edilir.
•Negatif sayılar üzerinde (–)
işareti ile gösterilir.
Düzlemler için Önemli noktalar
1. Doğrultuların tersine indisleri negatif olan
düzlemler aynıdır.
2. Doğrultuların tersine indisleri tam sayı ile
çarpılarak bulunan düzlemler birbirinden
farklıdır.
3. Kübik sistemde birbirinin aynı indise sahip
doğrultu ve düzlemler birbirine diktir.
4. Aynı özelliğe sahip düzlemler “düzlem ailesi”
oluştururlar. Büyük parantez ile ifade edilirler.
100  100, 010, 001.
{110}  (110), (011), (101), (110), (011), (101)
Düzlem A
1. x = 1, y = 1, z = 1
2. h=1/x = 1, k=1/y = 1,l=1 /z = 1
3. Kesir bulunmuyor.
4. (111)
Düzlem B
1. Düzlem z eksenini kesmez, x = 1, y = 2, z
=
2. h=1/x = 1, k=1/y =1/2, l=1/z = 0
3. Tam sayı olmalı: h=1/x = 2, k=1/y = 1,
l=1/z = 0
4. (210)
Düzlem C
1. Düzlem 0, 0, 0 dan geçiyor. ydoğrultusunda kaydırırsak. Then, x = , y
= -1, z =
2. h= 1/x = 0, k=1/y = 1, l=1/z = 0

3. (0 1 0)
4. Kesir bulunmamakta.
110 düzlem ailesi kaç farklı düzlemi ifade eder?
Doğrultuların tersine indisleri negatif olan düzlemler
aynıdır.
Bu nedenle Ailede 6 adet üye vardır.
Kafes düzlemlerinin gösterilmesi
Düzlem ailesi
Aynı özelliğe sahip düzlemler bir düzlem ailesi teşkil eder.Aile {100}
paranteziyle belirtilir.
Draw (a) the [121] direction and (b) the [210] plane in a
cubic unit cell.
(c) 2003 Brooks/Cole Publishing / Thomson
Learning™
29
Doğrultular arasındaki açı verkörel olarak hesaplanabilir.




D1  u1 a  v1 b  w1 c




D 2  u2 a  v2 b  w2 c
İki doğrunun skaler çarpımı:


D1  D2  D1  D2  cos 
D1  D2
u1  u2  v1  v2  w1  w2
cos  

1
2
2
2
2
2
D1  D2
u1  v1  w1 u2  v2  w2
İki doğrultu arasındaki açı
Doğrultularının Miller endisleri [uvw] ve [u’v’w’] olan iki
doğrultu arasındaki açı δ şu ifadeyle verilir:
cosδ = (uu’+vv’+ww’)/(√(u2+v2+w2).(u’2+v’2+w’2)
Bir düzlemin normalinin Miller endisleri ,düzlemin Miller
endisleriyle aynıdır.
Örnek : (111) düzleminin normali [111] dir.
Bir doğrultu bir düzlem içindeyse, doğrultu ve düzlemin
Miller endislerinin çarpımının toplamı
sıfırdır.
Örnek [ uvw ] doğrultusu (u’v’w’) düzlemi içindeyse
u.u’+v.v’+w.w’ = 0 dır.
Birim hücrede bulunan atom sayısı
Birim hücrede bulunan atom sayısını tarif eder (Atom
sayısı/hücre).
Hekzagonal kafes için Miller-Bravais indisleri (hkil)
(0110)
Dikkat:
HEGZAGONAL YAPIDA DÜZLEM ve DOĞRULTU
Yapının ADF = 0,74 olup KS = 12’dir. Önemli örnekleri: Ti, Zn, Mg, Be gibidir.
Düzlem için 4 indisli sistem –Miller-Bravais- kullanılmaktadır.
(h k i l) = a1, a2, a3, c eksenleri üzerindedir.
KURAL : h + k = - i olmalıdır.
Doğrultu için 3 indisli sistem kullanılmaktadır. [ h k i ]
Düzlem A
1. a1 = a2 = a3 = , c = 1
2. 1/a1 = 1/a2 = 1/a3 = 0, 1/c = 1
3. Kesir içermiyor
4. (0001)
Düzlem B
1. a1 = 1, a2 = 1, a3 = -1/2, c = 1
2. 1/a1 = 1, 1/a2 = 1, 1/a3 = -2, 1/c = 1
3. Kesir içermiyor
4. (11 2 1)
(c) 2003 Brooks/Cole Publishing /
Thomson Learning™
Doğrultu C
1. 2 nokta: 0, 0, 1 ve 1, 0, 0.
2. 0, 0, 1, -1, 0, 0 = 1, 0, 1
3. Kesir içermiyor.
4. 
[1 01]
Doğrultu D
1. 2 nokta 0, 1, 0 ve 1, 0, 0.
2. 0, 1, 0, -1, 0, 0 = -1, 1, 0
3. Kesir içermiyor.
4. [1 10]
Aşağıda verilen doğrultuların indislerini bulunuz.
(c) 2003 Brooks/Cole Publishing / Thomson
Learning
Figure 3.49 Directions in a cubic unit cell for
Problem 3.52.
37
Atomsal dolgu faktörü(ADF)
Birim hüçre içinde bulunan atomların toplam hacmının(katı küreler
farzediliyor) birim hücre hacmına oranıdır (Atomların hacmı/birim
hücre hacmı).ADF malzemenin ne kadar sıkı istiflendiğini gösterir.
Doğrusal atom yoğunluğu
Atom Merkezleri söz konusu doğrultu üzerinde bulunan
atomların (atom merkezinden geçmesi şartı ile) sayısı göz
önüne alınarak atomların doğrusal dizilme sıklıkları
hesaplanır(atom sayısı/doğrultu uzunluğu).
Düzlemsel atom yoğunluğu
Merkezleri söz konusu düzlem üzerinde bulunan atomlar
(atom merkezinden geçmesi şartı ile) göz önüne alınarak
atomların düzlemsel dizilme sıklıkları hesaplanır(atom
sayısı/düzlem alanı).
HMK ve YMK yapılarda [1 1] doğrultusunu ve ( 1 1 1 ) düzlemini çiziniz. Bu
doğrultu ve düzlemdeki atom yoğunluklarını kafes parametresini 1 A° kabul
ederek hesaplayınız.
METAL , SERAMİK
ve POLİMER
YAPILAR
METALLER
Hacım merkezli kübik(HMK) yapı
Figure 3.4 Hacim merkezli yapıkübik (a) Kafes noktaları;
(b)atomların gerçekteki istifi, (c) bir çok kafesin 3 boyutta
istifi.
a
R
a= 4R/√3
ADF = [(Atom sayısı/hücre).(Bir atomun hacmı)]
/ (Birim hücrenin hacmı)
ADF = 2x(4πR3/3)/a3
= 2x(4πR3/3)/(4R/√3)3
= 0,68
•Köşelerde ve merkezde birer atom bulunmaktadır.
•Bu yapıdaki metallerden bazıları; Fe (α-ferrit), V, Cr, Mo, W.
Birim kafesin %68 ‘i atomla
doludur, % 32’si boştur.
Yüzey merkezli kübik (YMK)yapı
•Köşelerde ve yüzey merkezlerinde birer atom bulunmaktadır.
•Bu yapıda metallerin bazıları; Fe (-ostenit), Al, Cu, Ni, vs.
a
R
2R
R
a= 4R/√2
ADF = 4x(4πR3/3)/a3 = 0,74
Hacmin % 74’ü dolu, % 26’sı boştur.
En yüksek doluluk oranı.
3.4 Yüzey merkezli kübik yapı (a) Kafes
noktaları; (b) atomların gerçekteki istifi, (c) bir
çok kafesin 3 boyutta istifi.
Sıkı düzen hekzagonal (SDH) yapı
-Köşelerde : 4x(1/12) = 1/3 ve 4x(1/6)= 2/3
Merkezde . 1 atom olmak üzere ,
birim hücrede toplam 2 atom bulunur.
-Sıkı düzen hegzagonal kafeste ADF= 0,74 tür.
-Bu değer YMK ile aynıdır.
-YMK de en yoğun düzlem (111), SDH de ise (0002) dir.
Seramikler
 Metal ve metal dışı elementlerin yaptığı
bağlarla oluşur.
 Dolayısıyla iyonik ve/veya kovalent
bağlara sahiptirler.
 Yüksek erime sıcaklığı - refraktörlük
 Kimyasal ve yüksek sıcaklıkta kararlılık
 Kırılganlık (Düşük kırılma tokluğu)
Şekil 1.5: Periyodik tabloda seramik malzemeleri oluşturan
metalik karakterde olan elementler (açık mavi) ve metal dışı
elementler (koyu mavi)
Seramik Malzemeler
• İki grupta incelenebilir:
– Kristal yapılı
– Amorf yapılı
• Seramikler metal ve metal olmayan elementlerin oluşturduğu
kimyasal bileşiklerdir.
• Farklı türleri mevcuttur:
MX
MX2
M2X3
M`M”X3
M`M”2X4
M: Metal element
X: Metal olmayan element
Seramiklerin kristal yapıları
Kimyasal bileşimleri ve yapıları metallerden çok farklı
olup inceleme bunlara göre yapılır.
Birim hücredeki iyon dizilişi elektriksel olarak nötr olacak şekildedir.
1-MX formüllü seramikler
-CsCl yapısı:Basit kübik yapıya sahiptirler.Birim hücre
başına 1 adet Cs+ ve 1 adet Cl- iyonu bulunmaktadır.
-NaCl yapısı
Her kafes noktasında iki iyon( Sodyum ve Klor) bulunan
bir YMK yapı söz konusudur.
Klor iyonları YMK kafesin normal kafes noktalarına
yerleşmiştir.Sodyum iyonları ise küpün kenarlarına ve
hacım merkezine yerleşir.
Na
Cl
2- MX2 formüllü seramikler
CaF2, SiO2 ,UO2, ThO2 ve TeO2 bu tür yapıya sahip
seramiklerdir.
-SiO2 nin yapısı
Silika mühendislikte yaygın olarak kullanılan
Bir malzemedir. Yeryüzünde bolca mevcuttur.
Karmaşık bir YMK yapıya sahiptir
(SiO4)-4 dört yüzlüsü
SiO2
3-M2X3 formüllü seramikler
Al2O3 (Alumina) nın yapısı
Yaklaşık olarak hekzagonal bir yapıya sahiptir.
4- M’M’’X3 formüllü seramikler
CaTiO3 yapısı
Basit kübik, yüzey merkezli kübik ve hacım merkezli
kübik yapılarının kombinasyonundan oluşmaktadır.
Perovskit olarakta bilinen bu yapıya bir tür
elektroseramik olan CaTiO3, ve elektro
seramik ve piezo elektrik özelliklere
sahip BaTiO3 örnek olarak verilebilir
(Basit
kübik,
YMK
ve
HMK
kombinasyonu).
(Köşelerde Ca+2; Y.merkezlerinde O-2 ve
Hacim merkezlerinde Ti+4 böylece her
kafes noktasında ve birim hücre başına
5’er iyon bulunur).
Grafit yapısı
Seramiklerin tanımına uymamakla birlikte (Bileşik teşkil
etmek) C nun bir kristal yapı hali olan grafit (Diğeri elmas)
de seramiklerin başlığı altında incelenir.
Levhalı bir yapıya sahip olan grafitin levha düzlemleri
içinde C atomları kovalent bağlarla bağlıdır. Buna karşılık
levhalar arası zayıf Van der Waals bağları mevcuttur. Bu
zayıf bağlar nedeniyle levhalar birbiri üzerinde kolayca
kayar. Grafit bu nedenle katı yağlayıcı olarak kullanılır.
Kovalent bağlarda 3 elektron kullanıldığından (Her karbon
atomu 3 karbon atomuyla kovalant bağ yapar), 4. elektron
levhalar arasında serbest kalmıştır. Bu serbest elektronlar
sayesinde grafit elektrik iletir (grafit elektrod).
Grafit’in kristal yapısı
Kuvvetli kovalent bağlar
Zayıf Van der Waals bağları
C atomları
Kristal olmayan yapılar (AMORF
YAPILAR): Camlar
Camlar: network yani ağ yapıya sahiptirler.
• Seramik camlar (Camlar): Amorf yapıdadırlar –kısa mesafede
düzenli yapıları vardır (short range ordered (SRO) structure)
(random network).
• Cam seramikler: Kristal camlardır – uzun mesafede düzenli
yapıları (long range order (LRO) structures) vardır.
Polimerler
•Hafiflik,
•Korozona ve kimyasallara karşı direnç,
•Düşük dayanım ve tokluk,
•Düşük rijitlik, yüksek elastiklik,
•Tekrar kullanılabilirlik (Recyclable),
•Elektrik yalıtkanlık.
Şekil 1.12: Periyodik tabloda polimer malzemeleri oluşturan
elementler.
Polimer Malzemeler
• Polimer yapılarda: uzun zincirler
• Belirli bir düzen oluşturmaları zor.
• Genelde kristal değillerdir.
• Bazı durumlarda zincirlerin belirli bir düzen
oluşturması ile kristal yapı oluşabilir.
• Ayrıca, çapraz bağ oluşumu ve dallanmalar
da olabilir. Bütün bunlar özellikleri etkiler.
The unit cell of crystalline
polyethylene.
Polimer Malzemeler:
Örnek:Polyetilen
PoliEtilen: -(C2H4)- yapısı
• C atomlarının oluşturduğu omurga:
•her C atomuna 2 H atomu bağlı .
• Bütün bağlar kovalent.
(b)
(a)
(d)
(c)
(a)
(b)
(c)
(d)
Lineer dallanmamış,
Lineer dallanmış,
Dallanmamış Termoset
Dallanmış Termoset
Polimerlerin kristal yapıları
Polimerlerin yapıları metal ve seramiklere
nazaran daha karmaşıktır.Burada uzun zincir molekülleri
olduğundan polimerlerin düzenli bir yapı oluşturması
zordur.
Kristalleşme ancak
bu zincirlerin uygun
düzenlenmeleri ile ,
yerel olarak ve en fazla
% 50 oranında
gerçekleşebilir.
X - Işını Difraksiyonu
• Ölçmede kullanılan teknik veya ekipman ne kadar hassas ise o kadar
küçük boyut ölçülebilir.
• Hassasiyeti kaba olan ölçü aletiyle, küçük ve hassas skalada ölçüm
yapılamaz.
• X-ışın difraksiyonu kristal yapıları ve dolayısı ile malzemeleri
tanımada kullanılabilir.
X-ışını difraksiyonu
•X-ışını tüpünden gelen ışın parça yüzeyine düşürülür. Yansıyan
ışın gelme ve yansıma açıları dikkate alınarak Ganiometre ile
ölçülür.
• X ışınlarının rastladığı her atomdan, aynı dalga boyunda fakat düşük şiddette ikincil
dalgalar saçılır. Küresel olarak yayılan bu dalgalar, aralarındaki girişim sonucu belirli
açılarda birbirini yok eder veya faz farkı dalga boyunun tam katı ise
kuvvetlendirirler.
•Bu pikler oluşumu diğer bir değişle yansıyan ışın
demetlerinin aynı fazda olması durumu “Bragg kuralı” nı
sağlar.
• : gelen ışının dalga boyu.
• d: düzlemler arası mesafe.
• : gelen ışın – düzlem arası açı.
• : Bragg açısı.
• h, k, l: düzlemin miller indisleri.
Bragg Kanunu
Yani piklerin oluştuğu BRAGG açıları ölçüm yapılan
kristal malzemenin belli atom düzlemelerini “d”
düzlemler arası mesafe parametresi yardımı ile ifade
eder.
nλ = 2dsinθ
nλ = 2d sinθ
Bragg kanunu
d hkl 
ao
h2  k 2  l 2
n: 1., 2. , 3. , n. mertebeden difraksiyon dalgalarını tanımlar.
Bragg kuralından d saptandıktan sonra yukarıdaki
formülden kafes parametresi saptanabilir.
θ açısına Bragg açısı; 2θ açısına difraksiyon açısı adı verilir.
• X-ışın difraksiyonu ile kristal yapıları, kafes parametresi ve atom çapı bulunabilir. Bu
parametreler, malzemenin özelliği olduğu ve her bir malzemede farklı değer aldığı için ilgili
element veya bileşikleri saptamada kullanılmaktadır.