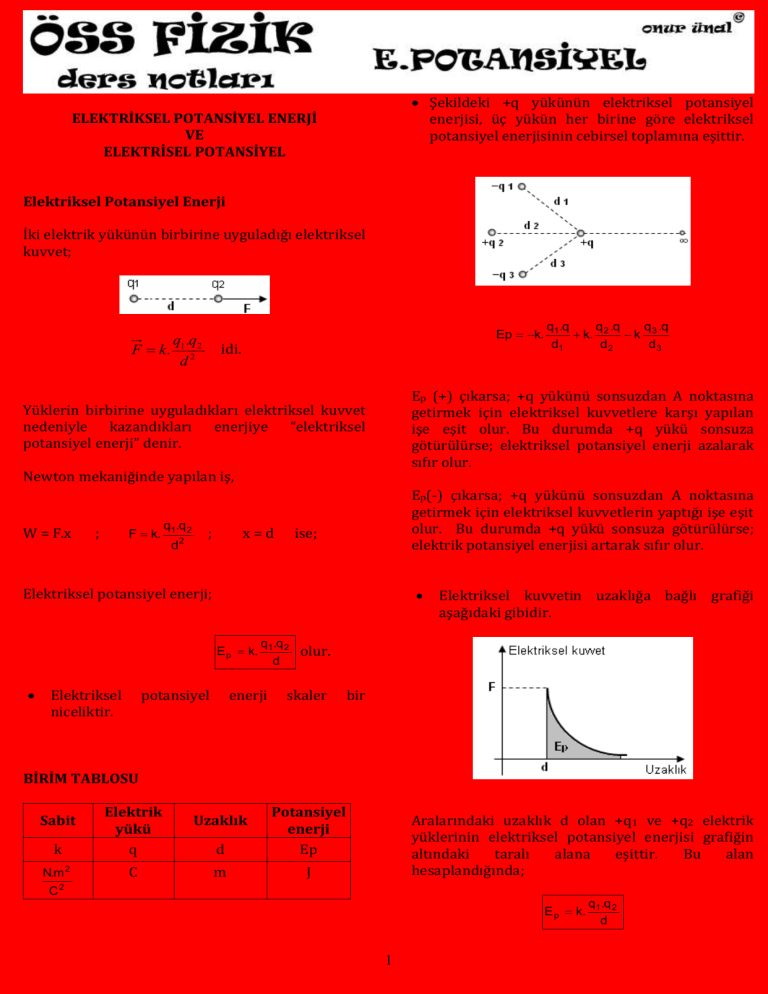
Şekildeki +q yükünün elektriksel potansiyel
enerjisi, üç yükün her birine göre elektriksel
potansiyel enerjisinin cebirsel toplamına eşittir.
ELEKTRİKSEL POTANSİYEL ENERJİ
VE
ELEKTRİSEL POTANSİYEL
Elektriksel Potansiyel Enerji
İki elektrik yükünün birbirine uyguladığı elektriksel
kuvvet;
F k.
q1 .q2
d2
Ep k.
idi.
Ep (+) çıkarsa; +q yükünü sonsuzdan A noktasına
getirmek için elektriksel kuvvetlere karşı yapılan
işe eşit olur. Bu durumda +q yükü sonsuza
götürülürse; elektriksel potansiyel enerji azalarak
sıfır olur.
Yüklerin birbirine uyguladıkları elektriksel kuvvet
nedeniyle kazandıkları enerjiye “elektriksel
potansiyel enerji” denir.
Newton mekaniğinde yapılan iş,
W = F.x
;
F k.
q1.q 2
d2
;
x=d
Ep(-) çıkarsa; +q yükünü sonsuzdan A noktasına
getirmek için elektriksel kuvvetlerin yaptığı işe eşit
olur. Bu durumda +q yükü sonsuza götürülürse;
elektrik potansiyel enerjisi artarak sıfır olur.
ise;
Elektriksel potansiyel enerji;
E p k.
Elektriksel
niceliktir.
potansiyel
q1.q 2
d
enerji
q .q
q1.q
q .q
k. 2 k 3
d1
d2
d3
Elektriksel kuvvetin uzaklığa bağlı grafiği
aşağıdaki gibidir.
olur.
skaler
bir
BİRİM TABLOSU
k
Elektrik
yükü
q
N.m 2
C
Sabit
C
d
Potansiyel
enerji
Ep
m
J
Uzaklık
Aralarındaki uzaklık d olan +q1 ve +q2 elektrik
yüklerinin elektriksel potansiyel enerjisi grafiğin
altındaki
taralı
alana
eşittir.
Bu
alan
hesaplandığında;
2
E p k.
1
q1.q 2
d
Aralarındaki uzaklık d olan +q1 ve +q2 yükünün
elektriksel potansiyel enerjisi,
E p k.
VA
Ep
q
;
E p k.
q1.q 2
d
ise;
Elektriksel potansiyel;
q1.q 2
d
V k.
q
d
Potansiyel skaler bir niceliktir. Birimi
Volt’tur. 1 volt; elektrostatik alanın herhangi
bir noktasındaki 1 coulomb’luk yükün
elektrik potansiyelidir.
BİRİM TABLOSU
Aralarındaki uzaklık d olan +q1 ve -q2 yükünün
elektriksel potansiyel enerjisi,
E p k.
Sabit
q1.q 2
d
k
N.m
2
Elektrik
yükü
q
C
d
Elektriksel
potansiyeli
V
m
Volt
Uzaklık
C2
Birden fazla yükün bir noktadaki elektriksel
potansiyeli;
Üç yükün A noktasındaki elektriksel potansiyeli; bu
yüklerin her birinin A noktasındaki elektriksel
potansiyellerinin skaler toplamına eşittir.
Elektriksel potansiyel enerji yüklerin birbirine
uyguladıkları kuvvetle doğru orantılıdır.
ELEKTRİKSEL POTANSİYEL
VA V1 V2 V3
Herhangi bir noktadaki +1 birimlik yükün
kazanacağı potansiyel enerjiye o noktanın
potansiyeli denir. Yani pozitif birim yük başına
düşen potansiyel enerji demektir.
VA
VA k.
q
q1
q
k. 2 k. 3
d1
d2
d3
A noktasındaki elektriksel potansiyeli bu işlem
sonunda pozitif ise, o noktasındaki pozitif birim
elektrik yük sonsuza giderken elektriksel kuvvetler
iş yapar, sonsuzdan o noktasına pozitif birim
elektriksel yük getirilirken elektriksel kuvvetlere
karşı iş yapılır.
Ep
q
A noktasındaki elektriksel potansiyeli bu işlem
sonunda negatif ise, o noktasındaki pozitif birim
elektriksel kuvvetlere karşı iş yapılır, sonsuzdan o
Herhangi bir q yükünden d kadar uzakta bulunan A
noktasındaki +1 birimlik yük başına düşen
potansiyel enerji o noktadaki elektriksel potansiyeli
verir.
2
noktasına pozitif birim elektriksel yük getirilirken
elektriksel kuvvetler iş yapar.
Elektriksel kuvvetlerin yaptığı iş negatiftir.
Elektriksel kuvvetlere karşı yapılan iş pozitiftir.
İki Nokta Arasındaki Potansiyel Fark
Pozitif birim yükü, elektrik alanın herhangi bir
noktasından, bir başka noktasına götürmek için,
elektriksel kuvvetlere karşı yapılan işe, bu iki nokta
arasındaki “potansiyel fark” denir.
VKL VL VK
Yüklü Bir Kürenin Elektriksel Potansiyeli
VKL k.
Yüklü bir kürenin
potansiyeli, kürenin
merkezinden
yüzeyine kadar hep
aynı
değerdedir.
Yüzeyden
uzaklaştıkça
ise
azalır.
WKL
q
q1
q
k. 1
d2
d1
ELEKTRİKSEL İŞ
q yükünü A noktasından B noktasına götürürken
yapılan elektriksel iş;
W AB VAB .q
W AB ( VB VA ).q
W AB q.VB q.VA
Ortak Potansiyel
Yüklü iki küre birbirine dokundurulduğunda
yükleri yarıçaplarıyla orantılı olarak paylaşırlar ve
potansiyelleri eşit oluncaya kadar aralarında yük
geçişi olur. Potansiyeller eşit hale geldiğinde yük
akışı durur.
Bu kürelerin ortak potansiyeli ise;
Vortak k.
q k. q1 q 2 ...
r1 r2 ...
r
3