Bileşke Kuvvet Çifti Momenti.

Mühendislik Mekaniği
Statik
Yrd.Doç.Dr. Akın Ataş
Bölüm 4
Kuvvet Sistemi Bileşkeleri
Kaynak: ‘Mühendislik Mekaniği: Statik’, R.C.Hibbeler, S.C.Fan,
Çevirenler: A. Soyuçok, Ö. Soyuçok.
4. Kuvvet Sitemi Bileşkeleri
Bölüm 3’te, bir parçacığın veya bir noktadan geçen bir kuvvet
sisteminin bileşkesinin sıfır, yani ΣF=0 olması gerektiği gösterildi.
Bölüm 5’te böyle bir kısıtlamanın bir rijit cismin dengesi için gerekli
ama yeterli olmadığı gösterilecektir.
Bir cisim bir büyüklüğe sahip olduğundan, ek kısıtlama, moment
kavramını ortaya çıkaran, uygulanan kuvvet sisteminin bir noktadan
geçmemesi durumu dikkate alınarak yapılmalıdır.
Moment bir cismi döndürmeye çalışır, denge ise cismin dönmemesini
gerektirir.
Bu bölümde, momentin formal bir tanımı verilecek ve bir kuvvetin,
bir nokta veya eksene göre momentini bulma yolları ele alınacaktır.
4.1 Vektörel Çarpım
Bir kuvvetin momentini belirlemeden önce vektörel çarpım yöntemini
öğrenmemiz gerekir.
A ve B vektörlerinin vektörel çarpımı,
C=AxB
şeklinde yazılır, «C eşittir A vektörel çarpım B» diye okunur.
Büyüklük. C’nin büyüklüğü, A ve B’nin büyüklükleri ve bunlar
arasındaki θ açısının sinüsünün çarpımı olarak tanımlanır. Buna göre,
C = ABsin θ’dır.
4.1 Vektörel Çarpım
Doğrultu. C vektörünün doğrultusu, A ve B’yi içeren düzleme diktir.
Yönü sağ el kuralına göre belirlenir.
C’nin doğrultu ve yönünü biliyorsak,
C = A x B = (ABsin θ)uc
yazabiliriz.
Burada, ABsinθ C’nin büyüklüğünü, uc birim vektörü
doğrultusunu tanımlar.
4.1 Vektörel Çarpım
İşlem Kuralları.
1. Değişme özelliği:
2. Skaler ile çarpım:
3. Dağılma Kuralı:
4.1 Vektörel Çarpım
Kartezyen Vektör Gösterimi.
C = A x B = (ABsin θ)uc
denklemi, kartezyen birim vektör çiftlerinin vektörel çarpımlarını
bulmada kullanılabilir.
4.1 Vektörel Çarpım
Kartezyen Vektör Gösterimi.
4.1 Vektörel Çarpım
Kartezyen Vektör Gösterimi.
4.1 Vektörel Çarpım
Kartezyen Vektör Gösterimi.
4.1 Vektörel Çarpım
Kartezyen Vektör Gösterimi.
4.2 Bir Kuvvetin Momenti – Skaler Gösterim
Bir kuvvetin bir noktaya veya bir eksene göre
momenti, kuvvetin bir cismi bu nokta veya
eksen etrafında döndürme eğiliminin bir
ölçüsüdür.
F kuvveti cıvatayı z ekseni etrafında döndürme
eğilimindedir.
Bu dönme eğilimine tork da denilir fakat
genellikle buna bir kuvvetin momenti veya
kısaca (Mo)z momenti denir.
4.2 Bir Kuvvetin Momenti – Skaler Gösterim
Moment ekseni
Mo momenti vektörel bir büyüklüktür,
çünkü belirli bir büyüklük ve doğrultuya
sahiptir.
Büyüklük.
Mo = Fd (N∙m, lb∙ft)
Doğrultu. Sağ el kuralı ile belirlenir. F ve
d’yi içeren düzleme dik ve yukarı doğru.
Dönme yönü
4.2 Bir Kuvvetin Momenti – Skaler Gösterim
Düzlemsel Kuvvet Sisteminin Bileşke
Momenti.
Bir kuvvet sistemi x-y düzleminde yer
alırsa, MRO momenti, bütün kuvvetlerin
momentlerinin cebirsel toplamı alınarak
belirlenebilir.
Örnek 4-1
Verilen her bir durum için, O noktasına göre momenti bulunuz.
Örnek 4-2
Şekilde gösterilen çubuk üzerine etkiyen
dört kuvvetin O noktasına göre bileşke
momentini belirleyiniz.
Örnek 4-2
Pozitif momentlerin +k yönünde, yani
saatin ters yönünde etkidiğini varsayarsak;
4.2 Bir Kuvvetin Momenti – Skaler Gösterim
Örneklerde de görüldüğü gibi, bir kuvvetin momenti her zaman
dönmeye neden olmaz. Örneğin, F kuvveti kirişi A mesnedi etrafında
MA = FdA momenti ile saat yönünde döndürmeye çalışır. Dönme,
ancak B mesnedi kaldırılırsa ortaya çıkar.
4.2 Bir Kuvvetin Momenti – Skaler Gösterim
Çivinin sökülebilmesi için O noktasına göre FH momentinin FN
kuvvetinin aynı noktaya göre momentinden daha büyük olması
gerekir.
4.3 Bir Kuvvetin Momenti – Vektörel Gösterim
Bir F kuvvetinin O noktasına veya
O’dan geçen ve O ve F’yi içeren
düzleme dik eksene göre momenti,
vektörel çarpım ile belirlenebilir.
Burada r, O’dan F’nin etki çizgisi
üzerinde yer alan herhangi bir
noktaya çizilen konum vektörünü
gösterir.
Moment ekseni
4.3 Bir Kuvvetin Momenti – Vektörel Gösterim
Moment ekseni
Moment ekseni
Büyüklük. MO = rFsinθ olarak bulunur. θ, r ve F vektörleri arasındaki
açıdır. r ve F vektörlerinin uygulama noktaları aynı değilse, aynı
noktaya uygulanacak şekilde tekrar çizilmelidirler.
Moment kolu d = rsinθ olduğundan,
4.3 Bir Kuvvetin Momenti – Vektörel Gösterim
Moment ekseni
Moment ekseni
Doğrultu. r ve F vektörlerinin uygulama noktalarının aynı olduğu
durumda sağ el kuralı ile belirlenir.
Vektörel çarpımın değişme özelliği olmadığından çarpım sırasının
korunması önemlidir.
4.3 Bir Kuvvetin Momenti – Vektörel Gösterim
Etki çizgisi
Kuvvetin Taşınabilirliği. F, kayan
vektör özelliğine sahiptir ve bu
nedenle etki çizgisi üzerindeki
herhangi bir noktaya etkiyebilir ve O
noktasına göre yine aynı momenti
üretir.
4.3 Bir Kuvvetin Momenti – Vektörel Gösterim
Kartezyen Vektör Formülasyonu.
Moment
ekseni
rx, ry ve rz O noktasından kuvvetin etki çizgisi üzerindeki herhangi bir
noktaya çizilen konum vektörünün x, y ve z bileşenleridir.
4.3 Bir Kuvvetin Momenti – Vektörel Gösterim
Kuvvet Sisteminin Bileşke Momenti.
Bir kuvvet sisteminin O noktasına göre
bileşke momenti, yukarıdaki denklemin
ardışık uygulaması sonucu oluşan vektörlerin
toplamı ile belirlenebilir.
Örnek 4-3
Şekilde gösterilen F kuvvetinin O noktasına
göre momentini belirleyiniz.
Örnek 4-3
Çözüm için rA veya rB kullanılabilir.
Örnek 4-3
Çözüm için rA veya rB kullanılabilir.
Örnek 4-4
Şekilde gösterilen çubuk üzerine üç
kuvvet etki etmektedir. Bu kuvvetlerin O
noktasındaki flanşa göre ürettikleri
bileşke momenti belirleyiniz.
Örnek 4-4
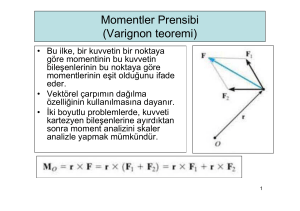
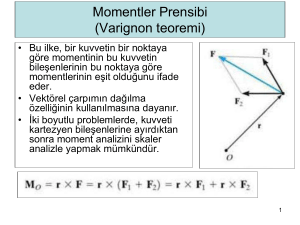
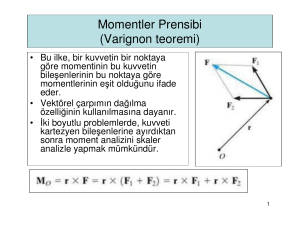
4.4 Momentler İlkesi (Varignon Teoremi)
Bir kuvvetin bir noktaya göre momenti, bu kuvvetin
bileşenlerinin bu noktaya göre momentlerinin
toplamına eşittir.
Örnek 4-5
Şekildeki kuvvetin O noktasına göre
momentini belirleyiniz.
Örnek 4-5
Çözüm I
Örnek 4-5
Çözüm II
Örnek 4-5
Çözüm III
Örnek 4-6
Şekildeki kuvvetin O noktasına göre
momentini belirleyiniz.
Örnek 4-6
Çözüm I (Skaler Analiz)
Örnek 4-6
Çözüm II (Vektörel Analiz)
4.5 Bir Kuvvetin Belirli Bir Eksene Göre Momenti
Bazı problemlerde, momentin belirli bir eksen üzerindeki bileşenini
bulmak önemlidir.
Skaler Analiz.
F kuvveti O’dan geçen moment
eksenine göre moment oluşturur.
Ama, bijonun dönüş eksenindeki
moment My momentidir.
Moment ekseni
4.5 Bir Kuvvetin Belirli Bir Eksene Göre Momenti
Vektörel Analiz.
F kuvvetinin y eksenine göre momentini
bulmak için öncelikle y ekseni üzerindeki
herhangi bir O noktasına göre F
kuvvetinin momenti bulunur:
Daha sonra skaler çarpım ile My
belirlenir:
4.5 Bir Kuvvetin Belirli Bir Eksene Göre Momenti
İzdüşüm ekseni
Örnek 4-7
Şekildeki kuvvetlerin x, y ve z eksenlerine
göre bileşke momentlerini belirleyiniz.
Örnek 4-7
Örnek 4-8
Şekilde gösterilen çubuk, A ve B’deki iki
kelepçe tarafından tutulmaktadır. F
kuvvetinin ürettiği, çubuğu AB ekseni
etrafında döndürmeye çalışan MAB
momentini belirleyiniz.
Örnek 4-8
4.6 Kuvvet Çiftinin Momenti
Kuvvet çifti, aralarındaki dik uzaklık d olan, aynı
büyüklükte ve zıt yöndeki paralel iki kuvvet olarak
tanımlanır. Çifti oluşturan kuvvetlerin bileşke kuvveti
sıfır olduğundan, çiftin tek etkisi belirli bir yönde
dönme veya dönme eğilimi üretmektir.
Kuvvet çifti ile üretilen momente kuvvet
çiftinin momenti denir. Bu moment
uzaydaki herhangi bir keyfi O noktasına
göre
belirlenen,
iki
kuvvetin
momentlerinin toplamına denktir.
4.6 Kuvvet Çiftinin Momenti
Skaler Formülasyon.
Vektörel Formülasyon.
4.6 Kuvvet Çiftinin Momenti
Denk Kuvvet Çiftleri.
Aynı momenti üreten iki kuvvet çiftine denk çiftler denir. Denk
çiftlerin kuvvetleri ya aynı düzlemdedir veya birbirine paralel
düzlemlerdedir.
4.6 Kuvvet Çiftinin Momenti
Bileşke Kuvvet Çifti Momenti.
Kuvvet çifti momentleri, serbest vektörler olduğundan, cisim
üzerinde herhangi bir noktaya uygulanabilir ve vektörel olarak
toplanabilirler.
Örnek 4-9
Şekilde gösterilen plakaya etki eden üç
kuvvet çiftinin bileşkesini belirleyiniz.
Örnek 4-9
Örnek 4-10
Dişli üzerine etki eden kuvvet çiftinin
büyüklüğünü ve yönünü belirleyiniz.
Örnek 4-10
Örnek 4-11
Şekilde gösterilen boruya etkiyen
kuvvet
çiftinin
momentini
belirleyiniz.
Örnek 4-11
Vektörel Analiz.
Örnek 4-11
Vektörel Analiz.
Kuvvet
çiftinin
momentlerini,
kuvvetlerden birinin etki çizgisi
üzerinde bir noktaya, örneğin, A
noktasına göre almak daha kolaydır.
Örnek 4-11
Skaler Analiz.
Problem üç boyutlu gösterilse
de, geometrisi M = Fd skaler
denklemini kullanmak için
yeterince basittir.
Örnek 4-12
Şekilde gösterilen boruya etkiyen iki
kuvvet çiftini bileşke kuvvet çifti
momenti ile değiştiriniz.
Örnek 4-12
Vektörel Analiz.
4.7 Kuvvet ve Kuvvet Çifti Sistemlerinin Basitleştirilmesi
Kuvvet, etki çizgisi boyunca A noktasından B noktasına taşınmıştır.
Yani, kuvvet, etki çizgisi boyunca herhangi bir A noktasında etki
edebildiğinden, kayan vektör olarak düşünülebilir.
Bir rijit cisim üzerinde, verilen bir noktada etkiyen bir kuvvet,
kuvvetin etki çizgisi üzerindeki başka bir noktaya uygulandığında,
cisim üzerindeki dış etkiler değişmez.
4.7 Kuvvet ve Kuvvet Çifti Sistemlerinin Basitleştirilmesi
Aynı prosedürü, bir kuvveti etki çizgisi üzerinde olmayan bir noktaya
taşımak için de kullanabiliriz.
İlgili noktaya öncelikle eşit ve zıt kuvvetler uygulanır. İki uçtaki ters
işaretli kuvvetler M = rxF momentine sahip kuvvet çiftini oluştururlar.
Kuvvet çifti momenti, serbest bir vektör olduğunda, cisim üzerindeki
herhangi bir noktaya uygulanabilir.
Örnek 4-13
Şekildeki yapı elemanı, gösterilen kuvvet
çifti momenti ve kuvvetlere maruzdur. Bu
sistemi, O tabanında etkiyen bir eşdeğer
bileşke kuvvet ve kuvvet çifti momenti ile
değiştiriniz.
Örnek 4-13
Örnek 4-13
4.8 Kuvvet ve Kuvvet Çifti Sisteminin Bileşkesi
=
=
M kuvvet çifti momenti, bir serbest vektör olduğundan, doğrudan
O’ya taşınır. F1 ve F2 kayan vektördür ve etki çizgileri O’dan geçmez.
Örneğin F1 O’ya uygulandığında, karşı gelen M1=r1xF1 kuvvet çifti
momenti de uygulanmalıdır.
FR’nin büyüklük ve doğrultusu O noktasının konumundan bağımsızdır.
Ancak, MRO bu konuma bağlıdır.
4.8 Kuvvet ve Kuvvet Çifti Sisteminin Bileşkesi
O’daki mesnet her iki durumda da aynı direnci göstermelidir.
Örnek 4-14
Şekilde gösterilen desteğe etkiyen
kuvvetleri, O noktasında etki eden bir
eşdeğer bileşke kuvvet ve kuvvet çifti
momentine indirgeyiniz.
Örnek 4-14
Kuvvet Toplamı.
Örnek 4-14
Moment Toplamı.
4.9 Kuvvet ve Kuvvet Çifti Sistemi için Ek İndirgeme
Bir Noktadan Geçen Kuvvet Sistemleri.
Bütün kuvvetler tek bir noktada etkir ve bileşke kuvvet çifti momenti
yoktur.
4.9 Kuvvet ve Kuvvet Çifti Sistemi için Ek İndirgeme
Düzlemsel Kuvvet Sistemleri.
Kuvvetlerin bulunduğu düzleme dik doğrultulu kuvvet çifti
momentleri içeren düzlemsel kuvvet sistemleri tek bir bileşke
kuvvete indirgenebilir.
4.9 Kuvvet ve Kuvvet Çifti Sistemi için Ek İndirgeme
Paralel Kuvvet Sistemleri.
Kuvvetlere dik kuvvet çifti momentleri içeren paralel kuvvet
sistemleri tek bir bileşke kuvvete indirgenebilir.
4.9 Kuvvet ve Kuvvet Çifti Sistemi için Ek İndirgeme
Dört kablo kuvveti de O noktasına etki eder. Dolayısıyla, bileşke
moment oluşmaz. Sadece FR bileşke kuvveti meydana gelir.
Bileşkenin mesnete yöneldiğine ve kulede eğilmeye sebep olmadığına
dikkat ediniz.
4.9 Kuvvet ve Kuvvet Çifti Sistemi için Ek İndirgeme
İki sistem de eşdeğerdir.
4.9 Kuvvet ve Kuvvet Çifti Sistemi için Ek İndirgeme
Vidaya İndirgeme.
Genel halde, cisme etkiyen kuvvet ve kuvvet çifti momenti sistemi, O
noktasında birbirine dik olmayan tek bir FR bileşke kuvveti ve (MR)O
kuvvet çifti momentine indirgenir. Ancak, (MR)O bileşenlerine ayrılarak
Mdik elimine edilebilir.
4.9 Kuvvet ve Kuvvet Çifti Sistemi için Ek İndirgeme
Vidaya İndirgeme.
Bu doğrudaş kuvvet ve kuvvet çifti momenti kombinasyonuna vida
adı verilir. Vida ekseni kuvvetle aynı etki çizgisine sahiptir.
Örnek 4-15
Şekilde gösterilen kuvvet ve
kuvvet çifti momenti sistemini
eşdeğer bir bileşke kuvvet ile
değiştiriniz ve etki çizgisinin
O’dan
ölçülen
mesafesini
belirleyiniz.
Örnek 4-15
Örnek 4-16
Şekilde gösterilen vince üç düzlemsel
kuvvet etki etmektedir. Bu yükü
eşdeğer bir kuvvetle değiştiriniz ve
bileşkenin etki çizgisinin AB kolonunu
ve BC ucunu kestiği yerleri belirleyiniz.
Örnek 4-16
Örnek 4-16
Örnek 4-17
Şekildeki tabaka dört paralel
kuvvete maruzdur. Verilen
kuvvet sistemine eşdeğer
bileşke kuvvetin büyüklük ve
doğrultusunu belirleyiniz ve
tabaka üzerindeki uygulama
noktasını bulunuz.
Örnek 4-17
Örnek 4-17
4.10 Basit Yayılı Yüklerin İndirgenmesi
Bazen cisimler yüzeylerine dağılmış olan
yüklere maruz kalabilirler. Örneğin, bir reklam
panosuna etki eden rüzgar basıncı gibi. Bu
yüklerin yüzey üzerindeki her bir noktadaki
şiddeti lb/ft2 veya N/m2 (Pa) birimleri ile
ölçülebilen p basıncı olarak tanımlanır.
Bu kesimde, üzerine yükün uygulandığı düz dikdörtgen cismin bir
ekseni boyunca düzgün olan yayılı basınç yüklerinin en genel
durumunu ele alacağız.
Basınç yükü şiddetinin yönü, yük şiddeti diyagramındaki oklarla
gösterilir.
4.10 Basit Yayılı Yüklerin İndirgenmesi
Yük fonksiyonu, p=p(x) Pa, basınç y ekseni boyunca düzgün
olduğundan, sadece x’in fonksiyonudur. b genişliği ile çarpılırsa,
w=w(x) N/m elde edilir (birim uzunluk başına kuvvet).
4.10 Basit Yayılı Yüklerin İndirgenmesi
Bileşke Kuvvetin Büyüklüğü.
Bu kuvvetler sistemi bir tek FR bileşke kuvvetine basitleştirilebilir ve
bu kuvvetin uygulama noktası belirlenebilir.
4.10 Basit Yayılı Yüklerin İndirgenmesi
Bileşke Kuvvetin Konumu.
Örnek 4-18
Şekilde gösterilen şaft üzerine etkiyen
bileşke kuvvetin büyüklüğünü ve
konumunu belirleyiniz.
Örnek 4-18
Örnek 4-19
Şekilde gösterilen kirişin üst yüzeyine
p=800x Pa yayılı yükü etkimektedir.
Bileşke kuvvetin büyüklüğünü ve
konumunu belirleyiniz.
Örnek 4-19
Örnek 4-20
Tanecikli malzeme şekilde gösterildiği
gibi
kiriş
üzerine
yayılı
yük
uygulamaktadır.
Bileşke
kuvvetin
büyüklüğünü ve konumunu belirleyiniz.
Örnek 4-20