Örnek sorular
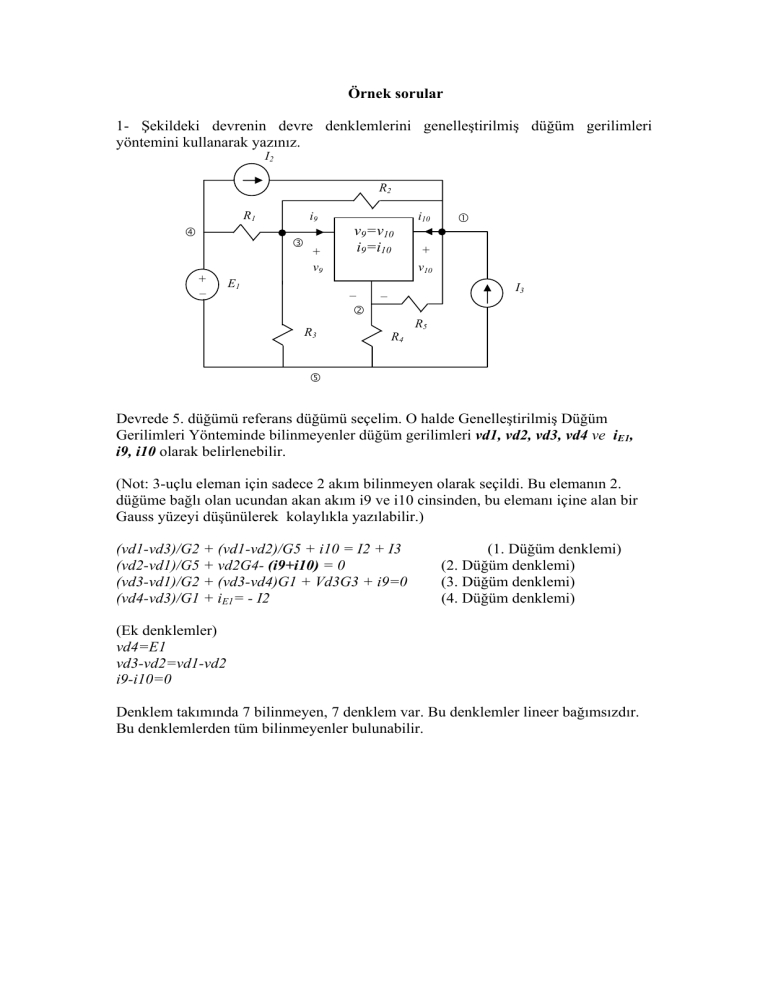
1- Şekildeki devrenin devre denklemlerini genelleştirilmiş düğüm gerilimleri
yöntemini kullanarak yazınız.
I2
R2
R1
f
i9
e
+
–
+
v9
E1
i10
v9=v10
i9=i10
–
d
R3
c
+
v10
I3
–
R5
R4
g
Devrede 5. düğümü referans düğümü seçelim. O halde Genelleştirilmiş Düğüm
Gerilimleri Yönteminde bilinmeyenler düğüm gerilimleri vd1, vd2, vd3, vd4 ve iE1,
i9, i10 olarak belirlenebilir.
(Not: 3-uçlu eleman için sadece 2 akım bilinmeyen olarak seçildi. Bu elemanın 2.
düğüme bağlı olan ucundan akan akım i9 ve i10 cinsinden, bu elemanı içine alan bir
Gauss yüzeyi düşünülerek kolaylıkla yazılabilir.)
(vd1-vd3)/G2 + (vd1-vd2)/G5 + i10 = I2 + I3
(vd2-vd1)/G5 + vd2G4- (i9+i10) = 0
(vd3-vd1)/G2 + (vd3-vd4)G1 + Vd3G3 + i9=0
(vd4-vd3)/G1 + iE1= - I2
(1. Düğüm denklemi)
(2. Düğüm denklemi)
(3. Düğüm denklemi)
(4. Düğüm denklemi)
(Ek denklemler)
vd4=E1
vd3-vd2=vd1-vd2
i9-i10=0
Denklem takımında 7 bilinmeyen, 7 denklem var. Bu denklemler lineer bağımsızdır.
Bu denklemlerden tüm bilinmeyenler bulunabilir.
2- Şekildeki devrenin denklemlerini genelleştirilmiş düğüm gerilimleri yöntemi ile
yazarak, devredeki bağımlı gerilim kaynağının gerilimini bulunuz.
5Ω
–
c
2.5Ω
+
2.5Ω
d
5Ω
5A
e
+
–
- v5Ω /3
f
Bağımlı kaynağın gerilimi 3. düğümün düğüm gerilimine eşittir.
Devrenin düğüm denklemleri aşağıdaki gibi yazılabilir:
(vd1-vd2)/2.5+(vd1-vd3)/5+vd1/5=0
(vd2-vd1)/2.5+(vd2-vd3)/2.5=5
(vd3-vd2)/2.5+(vd3-vd1)/5+Ibk=0
vd3= - (vd3-vd1) /3
(1. Düğüm denklemi)
(2. Düğüm denklemi)
(3. Düğüm denklemi, Ibk bağımlı
kaynağın akımı)
(Ek denklem)
Ek denklemden
vd1=4 vd3 bulunur.
Bu eşitlik 1. ve 2. düğüm denklemlerinde yerine konulursa (1. ve 2. Düğüm
denklemlerini 5 ile çarpmak işlemleri çok basitleştirmektedir)
vd3=1.25 V olarak bulunur.
v6=r6 iR3
3-
+ –
c
R8
R5
e
i1a
R4
+
–
i2b
g
f
d
e9(t)
g2
R1
R3
i7=g7 vR5
h
Şekildeki devre genelleştirilmiş düğüm gerilimleri yöntemi ile analiz edilecektir. Bu
amaçla devrenin düğüm ve ek denklemlerini yazınız (h'ıncı düğümü referans alınız).
Genelleştirilmiş Düğüm Gerilimleri Yönteminde bilinmeyenler
Düğüm gerilimleri Vd1,Vd2,Vd3,Vd4,Vd5 ve i1a,i2b,i6,i7,i9 akımları olacaktır. Bu nedenle
10 denklem yazmamız gerekir. Bunlardan 5 tanesi düğüm denklemleri, geri kalan 5
tanesi de jiratör, bağımlı kaynaklar ve bağımsız gerilim kaynağına ilişkin tanım
bağıntıları yardımıyla yazılacak ek denklemler olacaktır.
Düğüm denklemleri
c
d
e
f
g
(Vd1-Vd2)G8+i9=0
(Vd2-Vd3)G5+(Vd2-Vd1)G8+i6=0
(Vd3-Vd4)G4+(Vd3-Vd2)G5-i7=0
Vd4G3+(Vd4-Vd3)G4-i6+i1a=0
Vd5G1+i2b=0
Ek denklemler
Jiratörün tanım bağıntılarından:
i1a=gVd5
i2b=-gVd4
6. elemanın tanım bağıntısından
v6=r6iR3
Vd2-Vd4=r6Vd4G3
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
7. elemanın tanım bağıntısından
i7=g7vR5
i7= g7(Vd3-Vd2)
9. elemanın tanım bağıntısından
Vd1=e9(t)
(9)
(10)
R1 =2Ω
4- Şekilde verilmiş devrenin
Ik=7 A
a) Düğüm ve ek denklemlerini, elemanların
–
+
vx
c
R3 =1Ω
d
sayısal değerlerini kullanmadan yazınız.
e
+
+
–
b) Devredeki vÇ geriliminin değerini
Vk=4 V
vÇ
bulunuz.
R2 =3Ω
–
f
a) Şekildeki devrenin düğüm ve ek denklemlerini yazalım (Vd1,Vd2,Vd3, ib, ivk
bilinmeyenler).
c
d
e
-Ik+(Vd1-Vd3)G1+Ivk=0
(Vd2- Vd3)G3+ Vd2G2+Ik=0
(Vd3- Vd2)G3+(Vd3- Vd1)G1-ib=0
Ek denklemler:
Vd1=Vk
Ib=2Vx=2(Vd3-Vd1)
ivk: bağımsız gerilim
kaynağının akımı
b) Ek denklemleri ikinci ve üçüncü denklemlerde yerine koyalım.
⇒
(Vd2- Vd3)+ Vd2/3+7=0
Vd24/3-Vd3=-7
(Vd3- Vd2) +(Vd3-4)/2-2(Vd3-4)=0
⇒
⎡4 / 3 − 1 ⎤ ⎡Vd 2 ⎤ ⎡− 7⎤
⎢ − 1 − 1 / 2⎥ ⎢V ⎥ = ⎢ − 6⎥
⎣
⎦⎣ d3 ⎦ ⎣ ⎦
⎡Vd 2 ⎤ ⎡4 / 3 − 1 ⎤ ⎡− 7⎤ ⎡1.5⎤
⎢V ⎥ = ⎢ − 1 − 1 / 2⎥ ⎢ − 6⎥ = ⎢ 9 ⎥
⎦ ⎣ ⎦ ⎣ ⎦
⎣ d3 ⎦ ⎣
VÇ=Vd2=1.5 V
-Vd2-Vd3/2=-6
−1
⇒
ib=2 vx
5- Şekildeki devrenin Thevenin eşdeğerini elde ediniz.
Lineer cebrik çok-uçlular (lineer direnç elemanları, bağımlı kaynaklar, jiratör,
transformatör, vs) ve bağımsız kaynaklardan oluşan 2-uçlular (1-kapılılar)da, uç
gerilimi vab uç akımı i cinsinden
vab = Rth i + Vth
şeklinde yazılabilir. Bu denklemi gerçekleyen aşağıdaki devre verilen devrenin
Thevenin eşdeğeri olarak bulunur.
Rth
i
+
+
– Vth
vab
–
2-uçlu devrenin thevenin eşdeğerini bulmak için devrenin a-b uçları arasına değeri
i olan bağımsız akım kaynağı bağlanır ve vab gerilimi devredeki bağımsız
kaynaklar cinsinden yazılır.
d
+
vab
i
–
Yukarıdaki devre için genelleştirilmiş düğüm gerilimleri yöntemiyle aşağıdaki
denklemler kolaylıkla elde edilebilir.
vd /20 +(vd -25) /5 + (vd – vab)/4 – 3 – i = 0
i = (vab-vd)/4
(d düğümü için)
(a düğümü için)
Bu iki denklemden vd yokedilirse
vab = 8 i +32 olarak bulunur.
Buradan devrenin Thevenin Eşdeğeri aşağıdaki gibi bulunur.
8Ω
i
+
+
–
vab
32 V
–
6c
R1=5 Ω
d i1
i2
i1=v1/5
i2=(v1+0.5)0.5
+
E1=6 V
+
f
e
+
R3=2 Ω
v2
g
v1
e(t)=1+0.2cos2t V
–
E1=8 V
–
h
Şekildeki devrenin DC çalışma noktası analizi yapılacaktır. Bu amaçla yukarıdaki
devrede ne tür bir değişiklik yapılmalıdır?
a)
Bu elde ettiğiniz devrede
b) 3-uçlunun uç büyüklüklerinin devrenin çalışma noktasındaki değerlerini bulunuz.
3-uçluyu çalışma noktası civarında lineerleştirerek, şekildeki devrenin küçük
işaret eşdeğerini çiziniz.
c)
d) Devredeki v2 geriliminin değerini bulunuz.
Çözüm
a) Sorudaki devrenin çalışma noktası analizi için aşağıdaki devre çözülmelidir.
R1=5 Ω
IQ2
d IQ1
c
+
E1=7 V
f
i1=v1/5
i22=(v1+0.5)
e
+
VQ2
VQ1
–
R3=2 Ω
g
E1=8 V
–
h
b)
d numaralı düğüm için düğüm denklemi
IQ1+(VQ1-7)/5=0 olarak yazılabilir.
Ayrıca
IQ1=VQ1/5 denklemi kullanılırsa,
VQ1=7/2 V olarak bulunur.
Öte yandan IQ22=(VQ1+0.5) olduğundan, IQ22=4
⇒
Dikkat edilirse devrenin iki farklı çalışma noktası vardır.
e numaralı düğüm için düğüm denklemi yazılırsa
I1Q2=-2 V, I2Q2=2 V.
IQ2+(VQ2-8)/2 = 0 eşitliği elde edilir.
Buradan V1Q2= 12V ve V2Q2= 4V olarak elde edilir.
Üç uçlunun çalışma noktalarında uç büyüklüklerinin çalışma noktasındaki değerleri
(I1Q1=7/10 A, I1Q2=-2 A, V1Q1=7/2 V, V1Q2=12 V) ve
(I2Q1=7/10 A, I2Q2=2 A, V2Q1=7/2 V, V2Q2=4 V) olmaktadır.
b) 3-uçlu çalışma noktası aşağıdaki gibi lineerleştirilebilir:
~
~
i1=∂(v1/5)/∂v1 v1 + ∂(v1/5)/∂v2 v2 = v1/5
Q
Q
~
~
~
~
~
i2=∂((v1+0.5)0.5)/∂v1 v1 + ∂((v1+0.5)0.5)/∂v2 v2 = 0.5(VQ1+0.5)-0.5 v1=0.5/IQ2 v1
Q
Buradan 3-uçlunun iki çalışma noktasına karşı gelen iki farklı küçük işaret eşdeğeri
olduğu görülür.
Bunlardan birincisi
~
~
i1 = v1/5
~
~
~
i2=0.5/I1Q2 v1=-v1/4
diğeri de
~
~
i1 = v1/5
~
~
~
i2=0.5/I2Q2 v1=v1/4
Bunlardan birincisine karşı düşen devre aşağıda verilmiştir.
5Ω
~
i2
~
i
d 1
+
+
~
v1
0.2cos2t V
5Ω
e
+
~
v1/4
~
v2
–
–
~
Buradan v1 gerilimi
~
V1=0.2 cos2t /2=0.1 cos t V
~
v2=0.05 cos t V
olarak bulunur.
~
Sonuçta v2= V1Q2+ v2=12+0.05 cos t V olarak bulunur.
Diğer durum için de v2’nin değeri benzer şekilde
~
v2= V2Q2+v2=4 - 0.05 cos t V olarak bulunabilir.
2Ω