21.03.2014
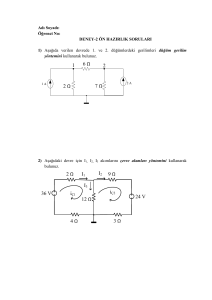
3.4. ÇEVRE AKIMLAR
YÖNTEMİ
3.4. ÇEVRE AKıMLAR YÖNTEMI (Ç.A.Y):
Bu yöntemde düğümlerdeki akımlar yerine,
çevredeki akımlar ele alınarak devrenin analizi
yapılır.
Yöntemin temel prensibi her bir bağımsız
çevrede Kirchoff’un gerilim kanunu uygulanır.
Bağımsız çevreler;
abefa, bcdeb
Bağımlı çevre;
abcdefa
1
21.03.2014
3.4. ÇEVRE AKıMLAR YÖNTEMI (Ç.A.Y):
Çevre akımları yöntemi aşağıda verilen üç adım
ile uygulanır:
1) Her bir bağımsız çevre için bir çevre akımı
yönü alınır. Bu akımların yönü keyfidir. (her ne
kadar keyfi denilse de genel tercih saat yönüdür)
2) Her çevreye KGK uygulanır. Gerilimler, çevre
akımları cinsinden tanımlanır.
3) Bağımsız çevre sayısı kadar elde edilen
denklemler düzenlenir.
3.4. ÇEVRE AKıMLAR YÖNTEMI (Ç.A.Y):
Örneğin şekildeki devre için; 1.adım olarak çevre akım
yönleri belirlenir.
2.adım olarak çevreye K.G.K. uygulanır.
1.çevre için;
veya
2
21.03.2014
3.4. ÇEVRE AKıMLAR YÖNTEMI (Ç.A.Y):
2.çevre için;
veya
3.adım olarak elde edilen denklemler matris formunda yazılır.
NOT: Çevre akımlarını dal akımlarından ayırmak için çevre akımları i, dal
akımları da I ile gösterilmektedir.
Bu devre için;
,
,
ÖRNEKLER
3
21.03.2014
3.5. BAĞıMLı/BAĞıMSıZ AKıM KAYNAKLARı
VARKEN Ç.A.Y:
Akım kaynağının bulunduğu çevreye göre iki durumdan söz
edilir:
1. Durum:
Akım kaynağı tek bir çevrede ise;
Birinci çevre için;
3.5. BAĞıMLı/BAĞıMSıZ AKıM KAYNAKLARı
VARKEN Ç.A.Y:
2. Durum:
Eğer bağımlı/bağımsız akım
kaynağı iki çevre arasında
ise (Şekil a);
Akım kaynağının bulunduğu dal
devreden çıkartılarak
SÜPERÇEVRE elde edilir (Şekil
b)
4
21.03.2014
SÜPER ÇEVRE
Örnek devre için;
1.adım; süper çevrede K.G.K.
Uygulanır.
NOT: Eğer devrede kesişen birden fazla süper çevre var ise
bu süper çevreler birleştirilir ve tek bir süper çevre haline
getirilir.
2.adım; yandaki devrede «0»
düğümünde K.A.K. uygulanır.
Bu iki eşitlik kullanılarak;
ÖRNEKLER:
5
21.03.2014
3.6. İNCELEME ILE DÜĞÜM VE ÇEVRE
ANALIZLERI
Bu yöntem Düğüm ve Çevre analizleri için
tanımlanmış kestirme bir yoldur.
Eğer devre sadece bağımsız akım
kaynaklarından oluşuyorsa, her bir düğüm için
KAK uygulanmasına gerek yoktur.
Diagonal üzerindeki terimler 1. ve 2.
düğüme bağlı dirençlerin toplamıdır.
Diagonalın dışındaki terimler ise 1.ve 2.
düğümlerin arasındaki iletkenliğin
tersidir.
Sağ taraftaki terimler ise 1. ve 2.
düğüme gelen ve çıkan akımların
toplamıdır.
3.6. İNCELEME ILE DÜĞÜM VE ÇEVRE
ANALIZLERI
Genelleştirilirse;
6
21.03.2014
3.6. İNCELEME ILE DÜĞÜM VE ÇEVRE
ANALIZLERI
Benzer şekilde çevre analizi içinde kısa bir yol
uygulanabilir.
Eğer devre yalnızca bağımsız gerilim
kaynaklarını içeriyorsa;
Diagonal üzerindeki terimler 1. ve 2. çevrelere bağlı
dirençlerin toplamıdır.
Diagonalın dışındaki terimler ise 1.ve 2. çevrelerin
arasındaki direncin tersidir.
Sağ taraftaki terimler ise 1. ve 2. çevrede saat yönlü
çevre akımına göre yazılan cebirsel toplamdır.
3.6. İNCELEME ILE DÜĞÜM VE ÇEVRE
ANALIZLERI
Genel olarak;
7
21.03.2014
ÖRNEK:
Devrenin düğüm
gerilimleri matrisini
yazınız.
ÖRNEK:
Devrenin çevre
akımları matrisini
yazınız.
8
21.03.2014
3.7. ÇEVRE VE DÜĞÜM YÖNTEMLERININ
KARŞıLAŞTıRıLMASı
Tüm elektrik devreleri Çevre Akımlar ve Düğüm
Gerilimleri yöntemleri ile çözülebilir.
Çözümleme aşamasında bilinmeyen sayısı yani
denklem sayısı değişiklik gösterir.
Bu nedenle çözümleme yöntemi seçiminde
devredeki bilinmeyen sayısının iyi belirlenmesi
gerekmektedir.
Ç.A.Y. ile herhangi bir devrenin çözümünde,
bilinmeyen sayısı çevre sayısı ile orantılıdır.
D.G.Y. ise devredeki düğüm sayısına bağlı olarak
bilinmeyen sayısı değişir.
ÇEVRE ANALIZINI ŞU DURUMLARDA;
Devrede
çok fazla seri eleman bulunuyorsa,
Gerilim kaynakları varsa,
Süper çevreler varsa,
En önemlisi de çevre sayısı düğüm
sayısından az ise
ÇAY çözümü daha kolay olandır.
Ayrıca, Çevre analizi yöntemi transistör devreleri
için tek uygun yöntemdir.
İşlemsel yükselteç (Op-amp) devreleri için aynı
şey söz konusu değildir.
9
21.03.2014
DÜĞÜM ANALIZINI ŞU DURUMLARDA;
Devrede,
Çok fazla paralel eleman varsa,
Akım kaynakları bulunuyorsa,
Süper düğümler varsa,
En önemlisi de düğüm sayısı çevre
sayısından az ise
DGY çözümü daha kolay olan yöntemdir.
Düzlemsel olmayan devreler için daha uygundur.
ÖRNEK:
10
21.03.2014
3.8. PSPICE ILE DEVRE ANALIZI
PSpice devre analizi için kullanılan sıklıkla
kullanılan bilgisayar programıdır.
Eğer devre eleman değerleri girilirse, dallardaki
akım ve gerilimleri hesaplar.
PSpice ile analiz devredeki elemanların şematik
çizimi ile başlar.
Düğüm gerilimleri şematik çizimde ilgili yere
‘VIEWPOINTS’ komutu konulması ile elde edilir.
Çalıştırmak için ‘Analysis/Simulate’ basılır.
3.8. PSPICE ILE DEVRE ANALIZI
11
21.03.2014
TRANSISTÖR DEVRESININ DC MODELI
Transistör devresinin analiz
yönteminden bahsedilecek.
Genel olarak kullanılan iki tip transistör
vardır. 1)Field Effect (FET) ve 2)Bipolar
Junction (BJT).
Bu derste yalnızca BJT ele alınacaktır.
Bir BJT elemanın 3 çıkışı vardır.
Bunlar gelen akım için base, çıkan akım
için colllector ve tüm akımlar için ortak
çıkış olan emmiter olarak adlandırılır.
TRANSISTÖR DEVRESININ DC MODELI
Bütün çıkışlardaki akımlar bir biri
ile ilişkilidir:
Base akımı ile collector akımları
arasında parametresi ile ilişkilidir.
değeri genelde 50-1000 arasında
değişir.
KGK BJT uygularsak:
12
21.03.2014
TRANSISTÖR DEVRESININ DC MODELI
Bir transistör devresinin eklenen gerilim/akıma bağlı olarak bir
çok modu vardır.
Bu derste sadece aktif mod çalışımı ele alınacaktır.
Bu mod gelen işareti yükseltmek için kullanılır.
Aşağıdaki şekil aktif modda çalışan BJT nin DC modelidir.
BJT ye düğüm gerilimi çözümü yalnızca DC modeli elde edilince uygulanabilir.
TRANSISTÖR DEVRESININ DC MODELI
Çözüm içi üç yol vardır:
1) Çevre analizi çözümü
Orijinal devre
2) Düğüm analizi çözümü
3) Pspice çözümü
13
21.03.2014
ÖRNEK:
, ve değerlerini devrenin
aktif modda çalıştığını, =50
ise hesaplayınız.
ÇÖZÜM:
Giriş çevresinde KGK;
0.7V ise
ve
arasındaki ilişki ile;
Çıkış çevresinde KGK;
14