Değişmez Küme

Dinamik Sistem
Zaman Durum
Dinamik sistem: (T, X, φt )
φt : X
X
a1) φ0=I
a2) φt+s =φt ◦ φs
▪
Gelişim
Fonksiyonu
Yörünge: Or(xo)
xo ilk koşulundan başlayan bir yörünge, x durum uzayının sıralı bir alt
kümesidir.

Or ( xo )  x  X : x   t xo , t T

Lineer otonom sistem
 x1  0  5  x1 
 x   1  2  x 
 2 
 2 
 x1   2  5  x1 
 x    1  4  x 
 2 
 2 
Lojistik dönüşüm
x(k  1)  3.46 x(k )(1  x(k ))
1
0.9
0.8
0.7
0.6
0.5
0.4
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Denge noktası- Sabit nokta:
 t x*  x* , t  T  x*  X
denge noktası-sabit nokta
Denge noktası-Sabit nokta nasıl belirlenir?
Sürekli Zaman
Çevrim:
x  f ( x)
x  f ( x)
0  f ( x* )
x*  f ( x* )
xo  Lo ,  t To xo   t xo ,  To  0, t T  L0
Sürekli Zaman
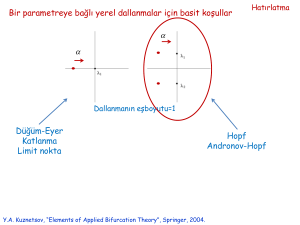
Y.A. Kuznetsov, “Elements of Applied Bifurcation Theory”3rd Edition, Springer, 2004,
Ayrık Zaman
periyodik yörüngesi
Çevrimdir.
Ayrık Zaman
Limit Çevrim:
Sürekli zaman, dinamik bir sisteme ait bir çevrimin komşuluğunda başka
bir çevrim yoksa bu çevrim Limit Çevrimdir.
Hangisi çevrim,
hangisi limit çevrim?
Faz Portresi:
Dinamik bir sistemin durum uzayının yörüngeler ile bölümlenmesi
faz portresini verir.  t x1
 t x2
Bu yörüngeleri birbirinden
farklı kılan nedir?
Faz portresine bakarak
neleri anlayabiliriz?
 t x3
Değişmez Küme (S) :
T , X , , S  X
t
 xo  S   t xo  S , t T
Değişmez küme sistemin asimptotik durumları
hakkında bilgi veriyor.
Dinamik sistemin yörüngelerini içeriyor ve
her yörünge bir değişmez küme.
Durum uzayı bir metrik uzay ise kapalı değişmez kümeleri tanımlayabiliriz.
En basit kapalı değişmez alt küme Denge noktası, limit çevrim
Manifold
Tuhaf çekici
Değişmez kümeleri gözlemeleyebilmemiz için
kolayca bulabilmemiz gerek, bu ne zaman olası?
Civarlarındaki yörüngeler de zaman ilerledikçe değişmez kümeye yaklaşırsa

Kararlı değişmez küme: T , X ,  t
Lyapunov anlamında kararlılık
X
tam metrik uzay
S 0 kapalı değişmez küme
Bu tanımı değişmez küme
tanımından farklı kılan ne?
S0  U ‘nun yeterince küçük herhangi bir U komşuluğunda
S0  V bir V komşuluğu var öyle ki  t x U , x V , t  0
S0  U 0 ‘nun bir U 0 komşuluğu vardır öyle ki t     t x  S0 , x U 0
Değişmez Küme (S) :
Asimptotik kararlılık
T , X , ,
t
SX
 xo  S   t xo  S , t T
Lyapunov anlamında kararlılık
Y.A. Kuznetsov, “Elements of Applied Bifurcation Theory”3rd Edition, Springer, 2004,
Lyapunov anlamında kararlılık nasıl tanımlanmıştı, hatırlayalım
Tanım: Lyapunov anlamında kararlılık
x (t )  f ( x(t )) sistemine ilişkin bir denge noktası xd
herhangi bir   0 için
x(t0 )  xd   ( )
eşitsizliği
olsun. Verilen
x(t )  xd   , t  t0, t  R
eşitsizliğini gerektirecek şekilde bir  ( ) bulunabiliyorsa xd denge
noktası Lyapunov anlamında kararlıdır.
Denge noktası xd kararlı olsun.
lim x(t )  xd  0
t 
ise
xd
denge noktası asimptotik kararlıdır.
Bir başka Lyapunov anlamında kararlılık
x  f ( x), x  R n
~
x (t ) verilen sistemin herhangi bir çözümü olsun
Tanım: Lyapunov anlamında kararlılık (Wiggens, sf.7)
x (t ) olsun. Verilen
x  f (x) sistemine ilişkin bir çözüm ~
herhangi bir   0 için y (t ) herhangi bir başka çözüm olmak üzere
~
x (t0 )  y(t0 )   ( )
eşitsizliği
~
x (t )  y(t )   , t  t0, t  R
~
eşitsizliğini gerektirecek şekilde bir  ( ) bulunabiliyorsa x (t ) çözümü
Lyapunov anlamında kararlıdır.
~
x (t ) kararlı olsun.
lim ~
x (t )  y(t )  0
t 
~
ise x (t ) çözümü asimptotik kararlıdır.
S. Wiggens, “Introduction to Applied Nonlinear Dynamical Systems and Chaos ”2nd Edition, Springer, 2003,
Bir Örnek
Strogatz, sf.16
x  sin x, x(0)  0
dx
dt

  sin x
t   ln
t  ln
1
 cot x  c
sin x
1  cot x0 sin x0 sin x
1  cot x sin x sin x0
x
x  0 x  0 x  0
x
x  0
x  0
x  0 x  0 x  0