Diren Dallanması

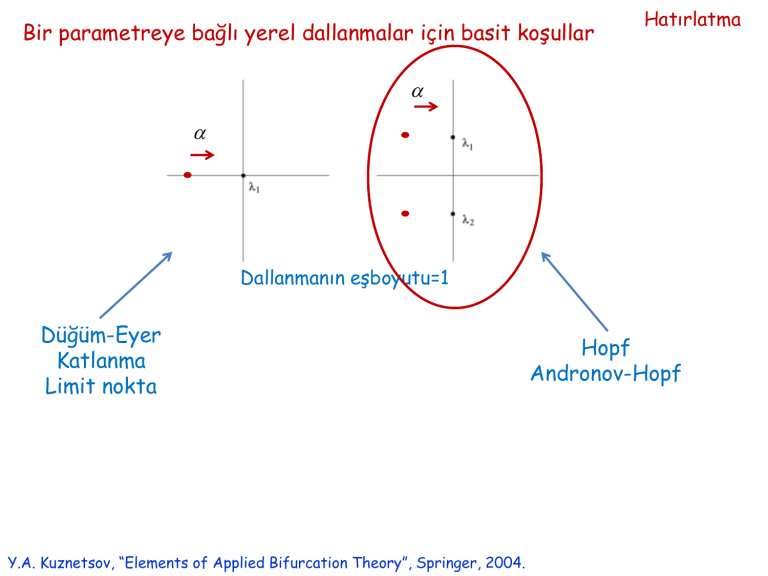
Bir parametreye bağlı yerel dallanmalar için basit koşullar
Hatırlatma


Dallanmanın eşboyutu=1
Düğüm-Eyer
Katlanma
Limit nokta
Y.A. Kuznetsov, “Elements of Applied Bifurcation Theory”, Springer, 2004.
Hopf
Andronov-Hopf
Hopf Dallanması
x  f ( x, ), x  R2 ,   R 
x1  x1  x2  x1 ( x12  x22 )
x2  x1  x2  x2 ( x  x )
2
1
2
2
Y.A. Kuznetsov, “Elements of Applied Bifurcation Theory”, Springer, 2004.
z ˆ x1  ix2

z ̂ e j
   (   2 )
  1
Hopf Dallanması
Teorem
x  f ( x, ), x  R 2 ,   R,
*
f  C  yeterince küçük tüm  ‘lar için x  0 ‘da  (0)  0,  (0)  0  0
özdeğerleri 1, 2 ( )   ( )  i ( ) olan denge noktası olsun.
(1) l1 (0)  0 l1 birinci Lyapunov katsayısı
( 2)  (0)  0

* Sistemini
d
d
 y1   
y   
 2 1
 1  y1 
4
2
2  y1 
 y   ( y1  y1 )  y   O( y )

  2 
 2
dönüştüren tersinir koordinat, parametre ve zamanı ölçekleyen
dönüşümler vardır.
Lemma
**
x1  x1  x2  x1 ( x12  x22 ) sistemi orijin civarında (**) sistemine topolojik
x2  x1  x2  x2 ( x12  x22 )
olarak eşdeğerdir.
http://www.scholarpedia.org/article/Andronov-Hopf_bifurcation
Bazı diğer yerel dallanmalar için koşullar
x  f ( x,  ), x  R,   R n
Uç Dallanması:
f xx ( x*,d )  0,
f ( x*,d )  
x* denge noktasının  d parametre değerinde bir
uç dallanma noktası olması için sağlaması gereken
koşullar aşağıdakilerdir:
f ( x*,d )  0
denge noktası
f x ( x*,d )  0
Hiperbolik değil
f xxx ( x*,d )  0
f x ( x*,d )  
Dallanma noktasında kuadratik
terimler içermemekte ancak kübik
terimler içermekte
Çaprazlık koşulu
ile tanımlanan  ve  lineer bağımsız
Uç Dallanması için önörnek:
x    x  x3
F.C.Hoppensteadt, E.M. Izhikevich, “Weakly Connected Neural networks”, Springer, 1997.
x  f ( x,  ), x  R,   R n
Diren Dallanması: x*  0 denge noktasının  d parametre değerinde bir
uç dallanma noktası olması için sağlaması gereken
koşullar aşağıdakilerdir:
f ( x*,d )  0
denge noktası
f x ( x*,d )  0
Hiperbolik değil
f xxx ( x*,d )  0
f x ( x*,d )  0
Dallanma noktasında kuadratik
terimler içermemekte ancak kübik
terimler içermekte
Çaprazlık koşulu
Diren Dallanması için önörnek:
x   x  x3
Hiperbolik olmazsa ne yapabiliriz?
x  f ( x), x  R n
x* hiperbolik olmayan denge noktası olsun
f x ( x* ) ‘in özdeğerlerinden
reel kısımları sol kompleks düzlemde
olanlara ilişkin özvektörlerin v1 , v2 ,..., vn oluşturduğu genelleştirilmiş
özuzay T s  span v1, v2 ,..., vn “kararlı altuzay”,



f x ( x* ) ‘in özdeğerlerinden
reel kısımları sağ kompleks düzlemde
olanlara ilişkin özvektörlerin vs 1, v2 ,..., vn oluşturduğu genelleştirilmiş

özuzay T u  span vn 1, v2 ,..., vn


 “kararsız altuzay”,
f x ( x* ) ‘in özdeğerlerinden
reel kısımları sıfır olanlara ilişkin
özvektörlerin vn 1, v2 ,..., vn0 oluşturduğu genelleştirilmiş özuzay

T C  span vn 1, v2 ,..., vn0

R  T T T
n
s
u
“merkez altuzay” ise
c
Neyi temsil ediyor?
Rn  T h  T c
x  f ( x), x  R n
x  f ( x), x  R n
*
¤
Teorem 11: (Merkez Manifold )
H : T c  T h , H (0)  0, H x (0)  0
R n ‘de x  0 ‘ın bir komşuluğu U olsun,


M  x  H ( x) x  T c manifoldu aşağıdaki özellikleri sağlıyorsa
“merkez manifold”’dur
(değişmezlik) M , U ‘nun komşuluğunda * veya ¤ için yerel olarak
değişmez kümedir.
u
(çekicilik) T  0 ise M yerel olarak çekici bir kümedir.
Y.A. Kuznetsov, “Elements of Applied Bifurcation Theory”, Springer, 2004.
Kaos’a varmanın yolları
Nasıl?
Düzen
Kaos
Umulmadık yapısal değişiklikler ile
Bu nasıl oluşabilir?
Ardışıl bir dizi dallanma ile, peryod katlanmasına yol açan
dallanmalar ile durum uzayındaki davranış değişmeye başlayıp
durum uzayında kalıcı çözüm tuhaf çekiciye dönüşebilir.
Bir örnek: Lorenz Sistemi
x   ( y  x)
y  x(   z )  y
x*  0,
y*  0,   R
z*  0,
z  xy  z
Denge noktaları
Hangi dallanma?
x*    (   1) ,
y*    (   1) ,   1
z*    1,
Lineerleştirelim: x*  0, y*  0, z*  0,
Özdeğerler
x  y  x
y  x  y
z    z
1  
Ne zaman kararlı, ne zaman kararsız ?
1
1
2,3     1 
(  1)2  4 (   1)
2
2
*
*
*
Lineerleştirelim: x    (  1) , y    (  1) , z   1
x  y  x
y  x  y   (   1) z
z    (   1) ( x  y )  z
Özdeğerler
3  (    1)2   (   )  2 (   1)  0
3  (    1)2   (   )  2 (   1)  0
Denge noktalarının var olması için
 1
olmalı
f ( )  0,   0

http://www.cg.tuwien.ac.at/~fischel/Lorenz97/raleigh.html
  0 .5
 6
http://www.cg.tuwien.ac.at/~fischel/Lorenz97/raleigh.html
  19
  24.1