bölme ve bölünebilme

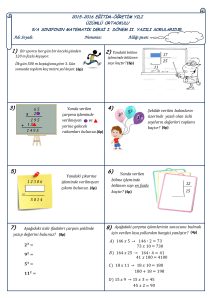
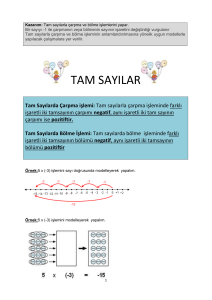
BÖLME VE BÖLÜNEBİLME
25 sayısını 6 ya böldüğümüzde bölüm 4 ve kalan 1 olur. Şekli inceleyin.
25 = 6 x 4 + 1
Bölünen = Bölen x Bölüm + Kalan
12312312 sayısını 123’e bölelim.
123 te 123 bir kere var. Sonra 1’i aşağı indiriyoruz. 1 de 123
olmadığı için bölüm tarafına bir sıfır ekliyoruz. 2’yi de aşağı
indiriyoruz. 12 de 123 olmadığı için bölüm tarafına bir sıfır daha
ekliyoruz. Şimdi 3’ü de aşağı indirdiğimizde 123’ü elde ettik ve
123 te 123 1 kere var. Bölüm tarafına bir tane 1 ekledik. Şuan
bölüm 1001 oldu. Devam ediyoruz. 1’i aşağı indiriyoruz. 1 de 123
yok bölüm tarafına bir sıfır daha 10010 oldu. 2’yi aşağı indiriyoruz. 12 de 123 yok ve Bölüm
tarafına bir sıfır daha ekledik.Bölüm 100100 oldu. Kalan ise 12 oldu.
Pratik yol
00100100 (olarak bulunur. Açıklaması aşağıda )
12312312 yazalım sonra 123 12312 deki 123 için 1 yazalım.
123 1 2312 1 için 0 yazalım 10 oldu.
123 12 312 ve 12 nin 2 si içinde bir sıfır daha 100 oldu
123 123 12 ve tekrar 123 oldu bunun içinde 1 ekleyelim 1001 oldu. 123123 12 ve tekrar 1
için 0. 10010 oldu. 2 içinde sıfır 100100 oldu Böleni bulduk. Kalan ise dikkatli bakın 12
dir.
Örnek : ABCDABCDABC sayısının ABCD ile bölümünde Bölüm ve Kalan Nedir.
Pratik çözümü kullanın. ABCD için 1 ve ABC için 3 tane 0 bu şekilde devam edin.
Bölüm = 10001000 olarak bulunur. Kalan ise ABC dir.
Unutmayın : Herhangi bir sayıyı örneğin 5’ e böldük Kalan 5 ten Küçük olmalıdır. Yani
kalan 0,1,2,3,4 olabilir. Taban aritmetiğine benziyor mu?
A sayısını 18 e böldüğümde Bölüm 10 Kalan 7 ise A sayısını rahatlıkla bulabiliriz. A = 18 x
10 + 7 = 187 dir.
Bölünebilme : Bir bölme işleminde kalan sıfır ise tam bölme ya da kalansız bölme yapılmış
demektir.
Bölme kurallarını kısaca anlatalım ve tablo oluşturalım.
(abcde) 5 basamaklı bir sayı olsun.
2 ile bölme Kuralı :
Kalan ={0,1} Bir sayı çift ise 2 ye kalansız (K=0) olarak bölünür. Tek ise bölme
işleminde kalan = 1 olacaktır. (e) yerindeki rakam çift ise 2’ye tam bölünür. Tek ise kalan 1
dir.
3 ile bölme kuralı :
Kalan = {0,1,2} Sayımızın rakamlarını toplarız 3 ün katı ise bu sayı 3 ile kalansız
bölünebilir. Yok 3 ün katından farklı ise bu topladığımız rakamları 3 böleriz kalan ne ise
Sayımızın kalanı da odur. a + b + c + d + e = 3k (3’ün katı. 0,3,6,9,12,15 gibi) olmalı
Örnek : 236574 sayısının 3 ile bölümünden kalan nedir.
Rakamları toplayalım. 2+3+6+5+7+4 = 27 3ün katıdır. Kalan sıfırdır. 28 olsa idi 3’ün
katından 1 fazla olacaktı K=1 ve 29 olsa idi 3’ün katından 2 fazla olacaktı. K=2 olurdu.
Diğer yöntem; Sayıları toplamadan önce rakamların içinde 3 ün katı ya da birkaç rakamı
hızlıca topladığımızda 3 ün katı varsa bu rakamları iptal ederiz. Az önceki örnekte; 236574, 3
ve 6, 3 ün katıdır bu rakamları atın. 2574, 2 ve 4 ün toplamı üçün katı bunu da atalım. 5 +7
de 3 ün katı, bunu da atalım geriye hiçbir şey kalmadığı için K=0 olacaktır.
4 ile Bölme Kuralı:
Kalan = {0,1,2,3}
Son iki basamak 4 ün katı olmalı. (de) 00, 04, 08, 12, 16, …, …, 92, 96 olmalı.
Ör. 1234567 sayısının 4 ile bölümünden kalan kaçtır.
67 inceleyeceğiz. 64, 4 ün katı 67’e 3 var kalan ise 3 tür.
5 ile Bölme Kuralı:
Kalan = {0,1,2,3,4}
Son basamak (Birler basamağı) 0 ya da 5 olacak.
Ör. 12345 in 5 ile bölümünden kalan 0 dır.
123458 in 5 ile bölümünden kalan 8 – 5 = 3 tür.
6 ile Bölme Kuralı:
Kalan = {0,1,2,3,4,5}
2 ve 3’e aynı anda bölünen bir sayı 6’yada bölünür. Diğer bir deyişle 3’e bölünen çift sayılar
6’yada bölünür.
Ör. 123456 (2 ye bölünüyor. 3 ü deneyelim. 3’e de bölünüyor o zaman 6’yada bölünür.)
Ör. 123461 (2 ye bölünmüyor. Bir düşüğünü yazalım ki çift olsun.)
123460 (2 ye bölünüyor. 3’e bölünmüyor. 2 daha inelim)
123458 (2 ye bölünüyor. Yine 3’e bölünmüyor. Bir daha 2 inelim.)
123456 (2 ve 3 bölünüyor.) Şimdi sorulan sayı ile bulduğumuz bu 6’ya bölünen sayıyı
çıkaralım. Fark 5 ve kalan da 5 olacaktır.
7 ile Bölme Kuralı:
Kalan = {0,1,2,3,4,5,6}
Ör. 123456 sayısının 7 ile bölümünden kalan nedir?
8 ile Bölme Kuralı:
Kalan = {0,1,2,3,4,5,6,7}
Son 3 basamak 8 in katı olacak. 000, 008, 016, 024, …, …, 992
Ör. ab345456def067 sayısının 8 ile bölümünden kalan kaçtır. Son üç basamağa bakalım. 067
8 in katı 64 tür.
67’e 3 var. K=3
9 ile Bölme Kuralı:
Kalan = {0,1,2,3,4,5,6,7,8}
Rakamları toplamı 9’un katı olmalı. a + b + c + d + e = 9k
Ör. 36452718 sayısının 9 ile bölümünden kalan kaçtır.
Pratik olarak yapalım. 9’un katlarını atalım. 3 ve 6 9’un katı at. 4 ve 5 9’un katı at. 2 ve 7
9’un katı at.1 ve 8 9’un katı at. Kalan=0 dır.
10 ile Bölme Kuralı:
Kalan = {0,1,2,3,4,5,6,7,8,9}
Birler basamağındaki rakam ne ise kalan odur.
Ör. 1234567 sayısının 10 ile bölümünden kalan 7 dir.
123450 10 ile bölümünden kalan 0 dır.
11 ile Bölme Kuralı:
Kalan = {0,1,2,3,4,5,6,7,8,9,10}
12 ile Bölme Kuralı:
Kalan = {0,1,2,3,4,…..,11}
3 ve 4’e bölünen her sayı (hem 3’e hemde 4’e bölünen) 12 ile tam bölünür. Burada kural 12
nin çarpanlarını bulmak ve bu çarpanlar arasında aralarında asal olan sayıları seçmek.
15 ile Bölme Kuralı:
Kalan = {0,1,2,3,4,…..,14}
3 ve 5’e bölünen her sayı (hem 3’e hem de 5’e bölünen) 15 ile tam bölünür.
20 ile Bölme Kuralı:
Kalan = {0,1,2,3,4,…..,19}
4 ve 5’e bölünen her sayı (hem 4’e hem de 5’e bölünen) 20 ile tam bölünür.
Ör. Bir sayının 45 ile bölünüp bölünemeyeceğini araştırıyorsunuz. 45’in çarpanlarına bakalım.
5 ile 9 aralarında asal. Demek ki hem 5’e hem de 9’a bölünen bir sayı 45 ile de tam bölünür.
Bölünebilme kurallarını dikkatlice okursanız bu tablo işinize yarayacaktır.