2 – SÜREKLİ RASSAL DEĞİŞKENLER Bir rassal deneme

2 – SÜREKLİ RASSAL DEĞİŞKENLER
Bir rassal deneme sonucunda elde edilen temel sonuçlar, belirli bir aralıktaki tüm
değerleri alabiliyorsa, sürekli bir rassal değişken tanımlanabilir. Zaman, uzaklık, sıcaklık
ölçüleri, gelir durumu gibi değişkenler sürekli rassal değişkenlerdir. Bu gibi değişkenlerin
temel özelliği, çok küçük parçacıklara bölünmüş aralıklarda, tek bir değeri alma olasılıklarının
son derece düşük olmasıdır. Örneğin bir aracın bir depo benzinle 152 kilometre 23 metre 35
santim 86 milimetre gitme ihtimali sıfıra yakındır. Bu durumda rassal değişkenlerin tek bir
değeri alma olasılığı yerine, bir değer aralığında olma ihtimalinin araştırılması daha sağlıklı
sonuçlar verecektir. Örneğin bir arabanın bir depo benzinle 151 – 153 kilometre arasında yol
yapma olasılığı, tek bir nokta erine, daha sağlıklı bir şekilde hesaplanabilir.
2 – 1 – Normal Olasılık Dağılımı
Özellikle insanların ağırlıklarının ve boy uzunluklarının tanımlandığı rassal
değişkenlerde, sınav sonuçlarında ve bunlara benzer rassal değişkenlerde sıklıkla kullanılan
bir dağılımdır.
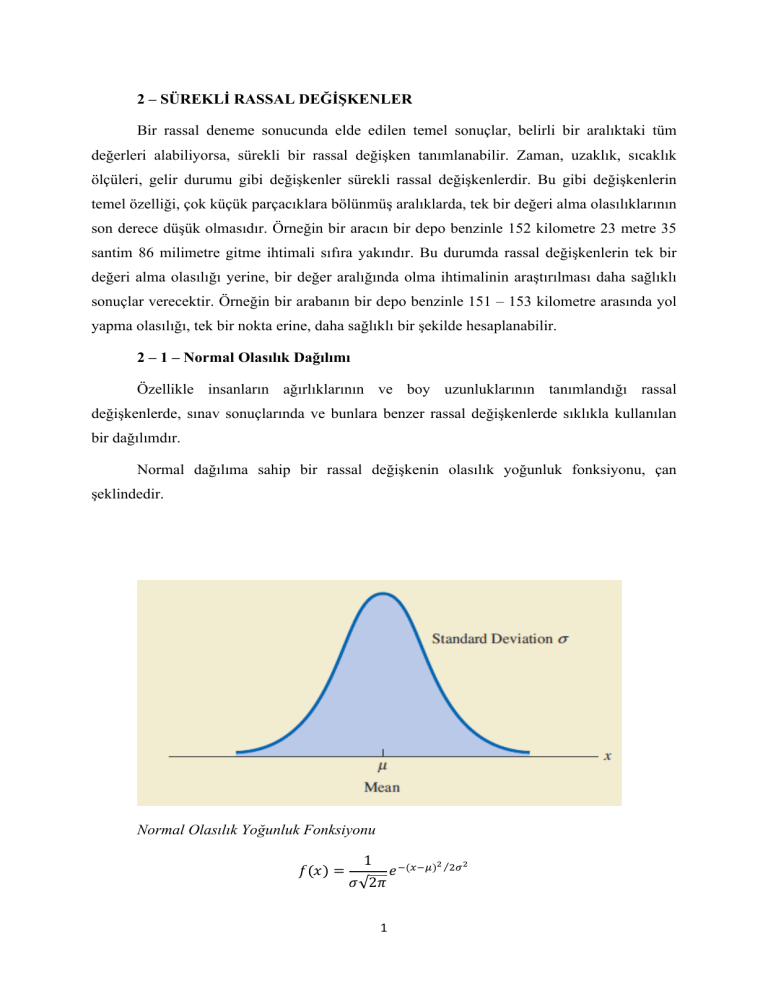
Normal dağılıma sahip bir rassal değişkenin olasılık yoğunluk fonksiyonu, çan
şeklindedir.
Normal Olasılık Yoğunluk Fonksiyonu
𝑓 𝑥 =
1
𝜎 2𝜋
𝑒 !(!!!)
1 !
!! !
Normal Dağılımın Özellikleri
1-Normal dağılıma sahip bütün rassal değişkenlerin sadece iki parametresi farklıdır:
Ortalamaları (𝜇) ve standart sapmaları (𝜎). Diğer bir ifadeyle, şayet her hangi bir veri seti
normal dağılım özelliği gösteriyorsa, ortalaması ve standart sapması ne olursa olsun, o veri
setindeki gözlem değerlerinin dağılımının şekli, çan eğrisi şeklinde olacaktır.
2-Normal dağılım eğrisinin en yüksek noktası (en yüksek olasılık değeri), ortalama
değerinde gerçekleşir ve aynı zamanda normal dağılımda ortalama değeri mod ve medyana da
eşittir.
3 - Normal dağılıma sahip rassal bir değişkenin ortalaması, negatif, pozitif bir değer
alabilir veya sıfır olabilir.
4 –Normal dağılım eğrisi, simetriktir. Ayrıca normal dağılım eğrisinin iki kuyruğu,
asimptotik olarak yatay eksende sonsuza gider (yatay eksenlere hiçbir zaman değmeyecektir).
Normal dağılım eğrisi simetrik olduğundan çarpık değildir (çarpıklık değeri sıfırdır).
5 –Normal dağılıma sahip rassal bir değişkenin ne kadar geniş veya dar bir dağılıma
sahip olacağını standart sapması belirler. Aşağıdaki şekilde ortalamaları aynı olan farklı iki
rassal değişkenin standart sapmaları farklı olduğu zaman olasılık dağılımlarındaki farklılık
temsil edilmektedir.
2 6 – Normal dağılıma sahip rassal değişkenin olasılık değerleri, normal dağılım
eğrisinin altında kalan alanın sayısal değeri hesaplanarak bulunur. Normal dağılım eğrisinin
altında kalan alanın toplam sayısal değeri “1”dir. Normal dağılım simetrik olduğundan,
ortalamanın sağında ve solunda kalan alanların sayısal değerleri birbirine eşittir ve 0.5’tir.
7 – Normal dağılıma sahip rassal bir değişkenin gözlem değerlerinin
yaklaşık % 68.3’ü ortalamanın “1” standart sapma sağında ve solunda
yaklaşık % 95.4’ü ortalamanın “2” standart sapma sağında ve solunda
yaklaşık % 99.7’si ortalamanın “3” standart sapma sağında ve solunda
yer alır.
3 2 – 2–Standart Normal Olasılık Dağılımı
Şayet normal dağılıma sahip rassal bir değişkenin ortalaması “0” ve standart sapması
“1” değerini alıyorsa, bu rassal değişkene standart normal dağılıma sahip rassal bir değişken
adı verilecektir. Normal dağılıma sahip bu rassal değişkenin değerleri “z” ile temsil
edilmektedir.
Standart Normal Olasılık Yoğunluk Fonksiyonu
𝑓 𝑥 =
1
2𝜋
𝑒 !!
!
!
Diğer bütün sürekli rassal değişkenlerde olduğu gibi standart normal dağılıma sahip
rassal bir değişkenin olasılık değerlerinin hesaplanabilmesi için, olasılık yoğunluk
fonksiyonun belirli bir aralıkta altında kalan alanın sayısal değeri hesaplanmalıdır. Standart
normal dağılıma sahip rassal bir değişkenin olasılık fonksiyonun altında kalan alanın sayısal
değeri, tablodan bulunabilir. Bunun için üç durumu inceleyeceğiz.
(a) Standart normal değişkenin belirli bir değere eşit ve bu değerden düşük olma
ihtimali
Standart normal dağılıma sahip rassal değişkenin “1” değerinden düşük olma ihtimali
nedir?
𝑃 𝑧 ≤ 1 =?
Bu sorunun cevabını bulurken tabloda z değerinin “1” olduğu yere gidilir ve bu
değerin karşısında yazan değer (0.8413), standart normal dağılım yoğunluk fonksiyonunun
altında kalan alanın sayısal değerine eşittir.
4 𝑃 𝑧 ≤ 1 = 0.8413
(b) Standart normal değişkenin belirli bir aralıkta olma ihtimali
Örneğin standart normal dağılıma sahip rassal değişkenin – 0.50 ile 1.25 değerleri
arasında olma olasılığı nedir?
𝑃 −0.5 ≤ 𝑧 ≤ 1.25 =?
Öncelikle standart normal değişkenin 1.25 değerinin altında kalan alanının sayısal
değerini bulalım. Dikkat edilirse tabloda z değerinin 1.2 olduğu yer, satılarda yer almaktadır.
Tablonun en üstündeki sütunda ise 0.5 değerine gidildiğinde bu iki değerin kesiştiği hücre, z
değişkeninin 1.25 değerini alma olasılığını verecektir.
𝑃 𝑧 ≤ 1.25 = 0.8944
5 Aynı şekilde z değişkeninin – 0.5 değerinden küçük olma ihtimalini bulalım. Dikkat
edilirse tabloda z değişkeninin negatif değerleri yer almamaktadır. Ancak bu her hangi bir
sorun çıkartmayacaktır. Zira z değişkeni ortalama etrafında simetrik dağıldığından artı ve eksi
değerlerinin olasılık değerleri aynı olacaktır. Bu durumda tabloda z değeri 0.5 olduğunda
olasılık değerinin 0.6915 olduğu görülecektir. Bunun anlamı, z değişkenin eksi sonsuzdan
gelip 0.5 değerine kadar geçtiği alanda her hangi bir değeri alma olasılığı (fonksiyonun bu
değer aralığında altında kalan alanın sayısal değeri) 0.6915’tir. Bizim aradığımız aralık - 0.5
değerinin üstünde kalan alanı içerisine almaktadır (−0.5 ≤ 𝑧 ≤ 1.25). Standart normal
dağılım eğrisinin altında kalan alanın toplam değeri “1” olduğuna göre, z değerinin 0.5 olma
ihtimalini “1” değerinden çıkartarak z değerinin – 0.5’ten küçük olma ihtimalini bulabiliriz.
1 − 𝑃 𝑧 ≤ 0.5 = 1 − 0.6915 = 0.3085
Bu değer, z değişkeninin 0.5’ten daha büyük değerler aldığında olasılık fonksiyonunun
altında kalan alanın sayısal değeri olduğu gibi, z değişkeninin – 0.5’ten büyük değerler alması
halinde olasılık fonksiyonunun altında kalan alanın sayısal değerine eşittir.
6 Sonuç olarak z değişkeninin (−0.5 ≤ 𝑧 ≤ 1.25) aralığında bir değer alma olasılığı:
𝑃 −0.5 ≤ 𝑧 ≤ 1.25 = 0.8944 − 0.3085 = 0.5859
sonucu elde edilir.
(c) Standart rassal değişkenin gözlem sayısının belirli bir oranının altında veya
üstünde kaldığı z değerinin bulunması
Örneğin z rassal değişkeninin % 10’u hangi z değerinin üstünde yer almaktadır?
Dikkat edilirse burada koyu mavi ile taralı alanın sayısal değeri verilmiş ve bu değerin hangi z
değerinden sonra başladığı sorulmaktadır. Öncelikle olasılık fonksiyonunun altında kalan
alanın sayısal değeri “1”e eşit olduğuna göre 1 – 0.10 = 0.90 olasılık fonksiyonunun belirli bir
z değerine kadar taradığı alanın sayısal değeri olmalıdır. Bu durumda standart olasılık
yoğunluk tablosunda “0.90” değerine karşılık gelen z değerini bulduğumda bu değerden sonra
olasılık fonksiyonunun taradığı alanın 0.10 olduğunu söyleyebiliriz.
7 Dikkat edilirse tabloda “0.90” değerine en yakın olasılık fonksiyon değeri “0.8997”
değeridir. Bu değere karşılık gelen z değeri (z = 1.28), aradığımız cevabı verecektir. Sonuç
olarak z değişkeninin 1.28 değerini aşma olasılığı yaklaşık % 10 olmuştur.
2 – 3 – Her Hangi bir Normal Dağılıma Sahip Rassal Değişkenin Olasılık
Değerlerinin Hesaplanması
Normal dağılıma sahip rassal bir değişkenin ortalamasını ve standart sapmasını
bilmemiz halinde bu rassal değişkenin olasılık dağılımı hakkında bilgi sahibi olabiliriz.
Öncelikle rassal değişkeni, standart normal dağılıma dönüştürürüz ve z değerini elde ederiz.
Sonra standart normal dağılım tablosunda elde edilen z değerine karşılık gelen olasılık
değerlerini yorumlayabiliriz. Normal dağılıma sahip bir rassal değişkenin, standardize
edilebilmesi için gerekli olan üç temel bilgi vardır: Rassal değişkenin ortalaması (𝜇), standart
sapması (𝜎) ve olasılığı istenen değeri (X):
𝑍=
𝑋−𝜇
𝜎
Örneğin normal dağılıma sahip rassal değişkenin ortalaması 10, standart sapması 2
olsun. Acaba bu rassal değişkenin 14 değerinden büyük olma ihtimali nedir?
Normal şartlar altında normal dağılıma sahip rassal değişkenin olasılık değerini
bulabilmek için, normal dağılım olasılık fonksiyonunda ortalama, standart sapma değeri ve
istenen değer (X) yerine yazılarak integral alınır. Ancak, yaklaşık olarak, normal dağılıma
sahip bu rassal değişkenin 14 değerini aşma olasılığı, standart normal dağılım tablosu yardımı
ile bulunabilir. Öncelikle yapılması gereken, verilen değerlerden hareketle standart normal
dağılım değeri (z) elde edilir:
8 𝜇 = 10 𝜎 = 2 𝑋 = 14
𝑍=
𝑋 − 𝜇 14 − 10
=
=2
𝜎
2
Bulmuş olduğumuz bu “2” değerinin anlamı, normal dağılıma sahip, ortalaması 10 ve
standart sapması 2 olan rassal değişkenin 14 değerini aşma olasılığı ile standart normal
dağılıma sahip rassal değişkenin “2” değerini aşma olasılığının aynı olduğudur.
𝑃 𝑋 ≥ 14 = 𝑃(𝑍 ≥ 2)
Standart normal dağılım tablosunda z değişkeninin 2 değerinden küçük olma ihtimali
0.9772 olduğuna göre, “2” değerini aşma olasılığı % 2.28 olacaktır.
𝑃 𝑍 ≥ 2 = 1 − 0.9772 = 0.0228
Örnek 1: Araç lastiği üreticisi bir firma, ürettiği lastikler ile ortalama 36500 km yol
yapılabileceğini ve standart sapmasının da 5000 km olduğunu savunmaktadır. Acaba bu
firmadan rassal olarak alınan lastiklerle 40000 km’den daha fazla yol yapma olasılığı nedir?
𝑃 𝑋 ≥ 40000 =?
Lastiklerin normal dağılım gösterdiği varsayımı altında, öncelikle bu verilenlerle z
değerini elde edelim:
𝜇 = 36500 𝜎 = 5000 𝑋 = 40000
𝑍=
𝑋 − 𝜇 40000 − 36500
=
= 0.7
𝜎
5000
Normal dağılıma sahip ortalaması 36500 ve standart sapması 5000 olan rassal bir
değişkenin 40000 değerini aşma olasılığı ile standart normal dağılıma sahip rassal değişkenin
0.7 değerini aşma olasılığı aynıdır:
𝑃 𝑋 ≥ 40000 = 𝑃(𝑍 ≥ 0.7)
Standart normal dağılım tablosunda z değişkeninin 0.7 değerinden küçük olma ihtimali
0.7580 olduğuna göre, “0.7” değerini aşma olasılığı % 24.20 olacaktır.
𝑃 𝑍 ≥ 0.7 = 1 − 0.7580 = 0.2420
9 Bu firmadan alınan lastiklerle 35000 ile 37500 km arasında yol yapma ihtimali nedir?
𝑃 35000 ≤ 𝑋 ≤ 37500 = 𝑃(
𝑃
35000 − 𝜇
37500 − 𝜇
≤𝑍≤
)
𝜎
𝜎
35000 − 36500
37500 − 36500
≤𝑍≤
= 𝑃(−0.3 ≤ 𝑍 ≤ 0.2)
5000
5000
𝑃 𝑍 ≤ 0.2 = 0.5793
𝑃 −0.3 ≤ 𝑍 = 1 − 𝑃 𝑍 ≤ 0.3 = 1 − 0.6179 = 0.3821
𝑃 𝑍 ≤ 0.2 = 0.5793
𝑃 −0.3 ≤ 𝑍 ≤ 0.2 = 0.5793 − 0.3821 = 0.1972
Bu firma tarafından üretilen lastiklerin belirli bir kilometrenin altında yol yapması
durumunda garanti kapsamına alınması düşünülmektedir. Üretilen lastiklerin % 10’u garanti
kapsamına alınmak istendiğine göre en düşük kaç kilometreye kadar garanti verilmelidir?
10 Lastikler belirli bir kilometrenin altında yol yaparsa, garanti kapsamına alınacaklardır.
Üretilen lastiklerin en fazla % 10’u garanti kapsamına alınmak istendiğine göre, öyle bir
kilometre değeri bulmalıyız ki, bu değerin altında üretilen lastiklerin % 10’u kalmalıdır.
Standart normal dağılım tablosunda 0.90 alanı tarayan z değeri 1.28’dir. Ortalamanın
altında kalan alan söz konusu olduğundan buradaki z değeri negatif alınmalıdır:
𝑍 = −1.28 → −1.28 =
𝑋 − 36500
5000
𝑋 = −1.28 ×5000 + 36500 = 30100
Bu firma, 30100 kilometrenin altında yol yapan lastikleri garanti kapsamına dâhil
etmelidir.
11