12. Hafta Ders Notları
GENEL TEKRAR
A – Veri Türleri
Anakütle bir bütünü temsil ederken; örneklem, bir bütünün sadece bir kısmını temsil
etmektedir. Anakütledeki gözlem sayısı N ile temsil edilirken; örneklemdeki gözlem sayısı n
ile temsil edilir.
𝑛≤𝑁
Anakütlenin bir özelliğini tanımlayan sayısal bir değere parametre denirken;
örneklemin bir özelliğini tanımlayan sayısal değere istatistik adı verilir.
Örnek: Sakarya Üniversitesi’nde okuyan 73.500 öğrenci mevcuttur. Bu öğrencilerin
not ortalaması 2,01 olarak tespit edilmiştir. Sakarya Üniversitesi’nde bulunan bir fakültenin
içerisinde yer alan bir bölüm ele alındığında, bu bölümde 420 öğrenci okumaktadır ve bu
öğrencilerin not ortalaması 2,23 olarak bulunmuştur.
Anakütle: Sakarya Üniversitesi’nde okuyan öğrenciler
Anakütle gözlem sayısı: 𝑁 = 73.500
Anakütle parametresi: Ortalama not
𝜇 = 2.01
Örneklem: Sakarya Üniversitesi’nde bulunan bir fakültenin içerisinde yer alan bir
bölümün öğrencileri
Örneklem gözlem sayısı: 𝑛 = 420
Örneklem için istatistik: Ortalama
𝑥 = 2.23
1 A – 1 – Verilerin Ölçümü
Bazı veriler sayısal değerler alırken; bazı veriler sayısal olmayan ölçümlerden oluşur:
A – 2 – Verilerin Ölçü Düzeyleri
Kullandığınız verilerin ölçü düzeyleri, istatistiksel olarak hangi ölçümleri
yapabileceğinizi ve hangi işlemleri uygulayabileceğinizi belirleyecektir:
Ölçüm Düzeyi
türündeki değişkenlerin sıralanması
nedir” sorusu
mümkün değildir.
Ordinal (Sıralı) Düzey
Kategoriler aralarında sıralanabilir.
Türkiye’deki üniversitelerin
Ancak kategoriler arası farklar
sıralaması, veya bir dersten
bulunamaz veya anlamsızdır.
alınan geçme notlarının
harfler ile temsil edilmesi.
Interval (Aralık) Düzeyi
Bu düzeydeki değişkenin değerleri
Isı ölçümleri: Isı, 0 derece
arasındaki fark, anlamlıdır. Ancak
olabilir. Ancak bu, ısının
doğal bir sıfır noktası yoktur ve
olmadığı anlamına gelmez.
değerlerin birbirine oranı anlamsızdır.
Ratio (Oran) Düzeyi
Bu düzeydeki değişkenin doğal bir
“Gelir düzeyiniz nedir?”
“0” noktası vardır ve değerleri
sorusunun cevabı, “0”
arasındaki oranlar anlamlıdır.
olabilir.
2 Sayısal
Bir anketteki “göz renginiz
Kategorik
Sadece kategorilerden oluşur. Bu veri
(Niceliksel) değişkenler
Örnek
(Niteliksel) değişkenler
Nominal (Kategorik) Düzey
Tanımı ve özellikleri
Korelasyon (Correlation) ve Nedensellik (Causality)
İki değişken arasında doğrusal ilişkinin yönü ve şiddeti, korelasyon katsayısı ile
ölçülmektedir. Ancak iki değişken arasında doğrusal bir ilişkinin varlığı, birbirleri arasında bir
nedensellik ilişkisi olduğu anlamına gelmeyecektir. Örneğin elde edilen mısır miktarı ile
yağan yağmur miktarı arasında pozitif yönlü bir korelasyon söz konusudur. Bu, “Elde edilen
mısır miktarı arttıkça yağan yağmur miktarı da artar” şeklinde bir nedensellik içermemektedir.
B – VERİLERİN SAYISAL ÖLÇÜMLERİ
B – 1 – Merkezi Eğilim Ölçüleri
: Bir veri setinde yer alan tüm değerlerin toplanmasını ifade eder.
X: Aynı özellikleri tanımlanmış gözlem değerlerinin oluşturduğu bir değişkendir.
Ortalama: Bir veri setinde yer alan bütün gözlem değerlerini dikkate alır ve gözlem
değerlerinin hepsine eşit ağırlık vererek, bu değerleri temsil edecek tek bir sayısal değer
türetir.
B – 2 – Değişimin Ölçülmesi
Varyans ve standart sapma ile yapılmaktadır.
Varyans: Bir veri setinde yer alan gözlem değerlerinin her birinin ortalamaya olan
uzaklığının ortalamasını temsil eden bir sayısal değerdir.
Standart Sapma: Varyansıın pozitif kareköküdür.
ANAKÜTLE
Ortalama (Mean, Average)
Varyans
Standart Sapma
𝜇=
!
𝜎 =
𝜎=
ÖRNEKLEM
!
!!! 𝑋
!
!
!!!
(𝑋! − 𝜇)
𝑁
!
!!!
(𝑋! − 𝜇)
𝑁
3 𝑋=
𝑁
𝑠! =
!
𝑠=
!
!!! 𝑋
𝑛
!
!!!(𝑋!
− 𝑋)!
𝑛−1
!
!!!(𝑋!
− 𝑋)!
𝑛−1
Örnek: Bir futbol ligindeki teknik direktörlerin maaşları, aylık olarak, aşağıdaki
gibidir:
Aylık Maaşlar (TL)
2350
1250
1590
1280
4920
9000
5300
3600
1380
2120
a) Bu veri seti, kesikli mi yoksa sürekli mi değerler almaktadır?
b) Bu veri setinin ölçüm düzeyini (nominal, ordinal, interval, ratio) tanımlayınız.
c) Bu veri setinin ortalamasını bulunuz.
d) Bu veri setinin varyansını ve standart sapmasını bulunuz.
4 C – OLASILIK
Rassal süreç: Hangisinin gerçekleşeceği konusunda bir kesinlik olmayan ve en az iki
sonuç içeren durumdur. Örneğin, Hilesiz bir zarın atılması.
Olay: Rassal süreç sonucunda ortaya çıkması ile ilgilenilen bir durumdur.
A olayı: Atılan zarın “1” gelmesi – 𝐴 = {1}
B olayı: Atılan zarın çift sayı gelmesi – 𝐵 = {2,4,6}
Örneklem uzayı: Rassal süreç sonucunda ortaya çıkabilecek olayların tamamıdır.
𝑆 = 1,2,3,4,5,6
Olasılığın Hesaplanması
A olayı için: 𝑃 𝐴 =
! !"#$ı !ç!"!# !"#$ç !"#ı!ı
B olayı için: 𝑃 𝐵 =
! !"#$ı !ç!"!# !"#$ç !"#ı!ı
!"#$%& !"#$ç !"#ı!ı
!"#$%& !"#$ç !"#ı!ı
!
=!
=
!
!
Ayrık – Bağdaşmaz (Disjoint) Olaylar
İki olayın aynı anda meydana gelmemesini ifade eder:
𝐴∩𝐵 =∅
Tümleyen olaylar
A olayının tümleyeni (𝐴), A olayının sonuçları dışında örneklem uzayında yer alan
bütün sonuçlardır. A olayı ile tümleyeni 𝐴 olayı, bağdaşmaz iki olaydır.
𝐴 = {2,3,4,5,6}
𝑃 𝐴 +𝑃 𝐴 =1
Bütünü Kapsayıcılık (Exhaustive Events)
Olaylar bağdaşmazsa ve sonuçlarının bir araya gelmesi örneklem uzayını veriyorsa, bu
olaylar bütünü kapsayıcıdır. A ve B olayı, bağdaşmaz olmasına rağmen, bütünü kapsayıcı
değildirler.
C olayı: Atılan zarın sonucu tek sayı gelir.
𝐶 = {1,3,5}
𝐵∪𝐶 =𝑆
Olasılığın kuralları
0 ≤ 𝑃(𝐴) ≤ 1
𝑃 𝐵 +𝑃 𝐶 =1
5 Olasılığın toplama kuralı
Şayet iki olay, aynı anda meydana gelebiliyorsa (ayrık değillerse):
𝑃 𝐴 ∪ 𝐵 = 𝑃 𝐴 + 𝑃 𝐵 − 𝑃(𝐴 ∩ 𝐵)
Şayet iki olay, aynı anda meydana gelemiyorsa:
𝑃 𝐴∪𝐵 =𝑃 𝐴 +𝑃 𝐵
Koşullu Olasılık
Şayet A olayının meydana gelmesi B olayının meydana gelme olasılığını etkiliyorsa, B
olayının olasılığı hesaplanırken A olayının meydana geldiği gerçeği de dikkate alınmalıdır:
𝑃 𝐵𝐴 =
!(!∩!)
!(!)
veya 𝑃 𝐴 𝐵 =
!(!∩!)
!(!)
İstatistiksel Bağımlılık
İki olay arasında bir etkileşim söz konusu ise, koşullu olasılık denkleminden hareketle,
olasılıkları arasında şöyle bir ilişki tanımlanabilir:
𝑃 𝐴 ∩ 𝐵 = 𝑃 𝐵 𝐴 𝑃(𝐴)
Veya
𝑃 𝐴∩𝐵 =𝑃 𝐴 𝐵 𝑃 𝐵
İstatistiksel Bağımsızlık
Şayet bir olayın olasılığı diğer bir olayın meydana gelmesinden etkilenmiyorsa,
koşullu olasılığı kendi olasılığına eşit olacaktır:
𝑃 𝐵 𝐴 = 𝑃(𝐵)
Veya
𝑃 𝐴 𝐵 = 𝑃(𝐴)
Bu durumda bu iki olayın aynı anda meydana gelme olasılığı, koşullu olasılık
denkleminden hareketle, şu şekilde tanımlanabilir:
𝑃 𝐴 ∩ 𝐵 = 𝑃 𝐴 𝑃(𝐵)
İki olay, ancak ve ancak, bu koşul altında istatistiksel olarak birbirlerinden
bağımsızdırlar.
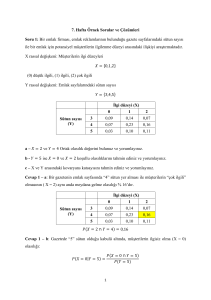
6 İki Değişkenli Olasılık
Bir fabrikada iki makine bulunsun. Bu makinelerin kurşun kalem üretimleri toplamda
1000 adet olup, makinelere dağılımı (kusurlu ve kusursuz olarak) aşağıdaki gibidir:
Kusurlu parça
Kusursuz parça
A makinesi
4
396
B makinesi
12
588
Bileşik Olay: Aynı anda iki farklı olayın meydana gelmesidir:
A olayı: A makinesi üretimi parçalar
B olayı: B makinesi üretimi parçalar
C olayı: Kusurlu parçalar
𝐶 𝑜𝑙𝑎𝑦ı: Kusursuz parçalar
Hem kusurlu hem de A makinesinde üretilmiş kaç ürün vardır?
𝐴∩𝐶 =4
Hem kusurlu hem de B makinesinde üretilmiş kaç ürün vardır?
𝐵 ∩ 𝐶 = 12
Marjinal olasılık (Kenar olasılığı)
Sadece tek bir olayın olasılığıdır.
C olayı: Kusurlu parçalar
Kusurlu parça sayısı = (A makinesinden) + (B makinesinden) = 4 + 12 = 16
Bu fabrikada üretilen kalemler arasından rassal olarak çekilen bir kalemin kusurlu
olma olasılığı nedir?
𝑃 𝐶 =
𝑡𝑜𝑝𝑙𝑎𝑚 𝑘𝑢𝑠𝑢𝑟𝑙𝑢 𝑝𝑎𝑟ç𝑎 𝑠𝑎𝑦ı𝑠ı
16
=
𝑡𝑜𝑝𝑙𝑎𝑚 𝑘𝑎𝑙𝑒𝑚 𝑠𝑎𝑦ı𝑠ı
1000
Koşullu Olasılık
Rassal olarak seçilen bir ürün kusurlu ise, bu kalemin A makinesinde üretilmiş olma
olasılığı nedir?
Koşul: Ürün kusurlu (C olayı)
Aranan olasılık: A makinesinde üretilmiş olma olasılığı (A olayı)
𝑃 𝐴𝐶 =
𝑃(𝐴 ∩ 𝐶) 𝐻𝑒𝑚 𝑘𝑢𝑠𝑢𝑟𝑙𝑢 ℎ𝑒𝑚 𝐴 𝑚𝑎𝑘𝑖𝑛𝑒𝑠𝑖𝑛𝑑𝑒 𝑘𝑎𝑙𝑒𝑚 𝑠𝑎𝑦ı𝑠ı
4
=
=
= 0,25
𝑃(𝐶)
𝐾𝑢𝑠𝑢𝑟𝑙𝑢 𝑘𝑎𝑙𝑒𝑚 𝑠𝑎𝑦ı𝑠ı
16
7 D – RASSAL DEĞİŞKENLER
D – 1 – Kesikli Rassal Değişkenler
Örneğin, gün içerisinde bir doktora gelen hasta sayısı, bir kutudaki arızalı parça sayısı
gibi.
Rassal değişken, tanım kümesi bir sürecin örneklem uzayı, değer kümesi reel sayılar
kümesi olan bir sayılar kümesidir.
Hilesiz iki zar aynı anda atılsın. Bu rassal süreç sonucunda oluşacak sonuçlar
(örneklem uzayı), aşağıdaki gibidir:
1,1 , 1,2 , 1,3 , 1,4 , 1,5 , 1,6 , 2,1 , 2,2 , 2,3 , 2,4 , 2,5 , 2,6 , 3,1 , 3,2 , 3,3 , 3,4 , 3,5 , 3,6 , 4,1 , 4,2 , 4,3 , 4,4 , 4,5 , 4,6 , 5,1 , 5,2 , 5,3 , 5,4 , 5,5 , 5,6 , 6,1 , 6,2 , 6,3 , 6,4 , 6,5 , 6,6
Şimdi bu tanım kümesinden hareketle elde edilecek olan rassal değişkeni ve değer
kümesini tanımlayalım.
X: Aynı anda atılan iki zarın toplamı
𝑋 = 2,3,4,5,6,7,8,9,10,11,12
Kesikli rassal değişkenin olasılık dağılımı
Kesikli rassal değişkenin bir değeri alma olasılığını ifade eder.
𝑃(𝑋 = 𝑥)
Örneğimizdeki X rassal değişkeninin alabileceği 11 farklı değer vardır. Her bir değerin
gerçekleşme olasılığı ise, tanım kümesinde bu toplamlara denk elen ikililerin sayısı ile
ilgilidir:
X
2
3
4
5
6
7
P(X = x)
1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36
8 8
9
10
11
12
Kesikli Rassal Değişkenin Ortalaması (Beklenen Değeri)
𝐸 𝑋 =
𝐸 𝑋 =
𝑋𝑃(𝑋 = 𝑥)
1
+ 3
36
𝑋𝑃(𝑋 = 𝑥) = 2
2
+ ⋯ + 12
36
1
=7
36
Kesikli Rassal Değişkenin Varyansı
𝜎 ! = 𝐸[𝑋 ! ] − 𝐸(𝑋)!
𝐸[𝑋 ! ] =
𝑋 ! 𝑃 𝑋 = 𝑥 = (2)!
1
+ 3
36
𝜎 ! = 𝐸[𝑋 ! ] − 𝐸 𝑋
!
!
2
+ ⋯ + 12
36
= 54.83 − 7
!
= 5.83
Alternatif Varyans hesaplama yöntemi
𝜎! =
[𝑋 − 𝐸 𝑋 ]! 𝑃(𝑋 = 𝑥)
Kesikli Rassal Değişkenin Standart Sapması
𝜎=
𝜎 ! = 5.83 = 2.414
9 !
1
= 54.83
36
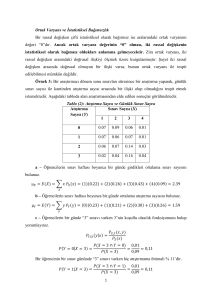
Kesikli Rassal Değişkenler ve Kovaryans
Kovaryans katsayısı, iki rassal değişken arasındaki doğrusal ilişkinin varlığını ve yönünü
tespit edebilir. Ancak iki rassal değişken arasında doğrusal olmayan ilişki formalarını tespit
edemez. Ayrıca doğrusal ilişkinin varlığını ve yönünü tespit etse bile, doğrusal ilişkinin
şiddetini de ölçemez.
𝐶𝑂𝑉 𝑋, 𝑌 = 𝐸 𝑋𝑌 − 𝐸 𝑋 𝐸(𝑌)
𝐸 𝑋𝑌 =
𝑥𝑦𝑃(𝑋 = 𝑥 ∩ 𝑌 = 𝑦)
!
!
Kovaryansın sayısal değer sınırları
−[𝑉𝑎𝑟 𝑋 𝑉𝑎𝑟 𝑌 ] ≤ 𝐶𝑂𝑉 𝑋, 𝑌 ≤ 𝑉𝑎𝑟 𝑋 𝑉𝑎𝑟(𝑌)
Y Değişkeni
X değişkeni
𝐸 𝑋 =
𝐸 𝑌 =
𝐸 𝑋𝑌 =
1
2
3
1
0.25
0.25
0
2
0
0.25
0.25
𝑥𝑃 𝑋 = 𝑥 = 1 0.50 + 2 0.50 = 1.50
𝑦𝑃 𝑌 = 𝑦 = 1 0.25 + 2 0.50 + (3)(0.25) = 2.00
𝑥𝑦𝑃 𝑋 = 𝑥 ∩ 𝑌 = 𝑦
!
!
= 1 1 0.25 + 1 2 0.25 + 1 3 0 + 2 1 0 + 2 2 0.25
+ 2 3 0.25 = 3.25
𝐶𝑂𝑉 𝑋, 𝑌 = 𝐸 𝑋𝑌 − 𝐸 𝑋 𝐸 𝑌 = 3.25 − 1.5 2.0 = 0.25
Kovaryans katsayısı “0” olmadığı için iki değişken arasında doğrusal bir ilişki olduğu
anlaşılır. Kovaryans katsayısı pozitif olduğu için iki rassal değişken arasında pozitif yönlü
doğrusal bir ilişki olduğu anlaşılır. Ancak ilişkinin güçlü mü yoksa zayıf mı olduğuna,
kovaryans katsayısına bakılarak karar verilemez. Ayrıca kovaryans katsayısı, nedensellik
(hangi değişken diğerini etkiler) ile ilgilide bir bilgi vermemektedir.
10 Bernoulli (İki terimli) olasılık dağılımı
Temel varsayımları
(a) Bir olayın sonucunda “başarı” ve “başarısızlık” olmak üzere iki temel sonuç
vardır.
(b) Başarı olasılıkları p ve başarısızlık olasılıkları (1 − 𝑝) her bir deneme için sabittir.
(c) Toplam n tane deneme içerisinde ilgilenilen x tane başarı vardır.
(d) Her bir denemede oluşan sonuçlar, birbirinden bağımsızdır.
𝑃 𝑋=𝑥 =
𝑛!
𝑝 ! (1 − 𝑝)!!!
𝑥! 𝑛 − 𝑥 !
Örnek: Bir yumurta firması yumurtalarını 30’lu kolilerde satışa sunmaktadır.
Firmanın verilerine göre yumurtaların % 95’i kırılmadan müşterilere ulaştırılmaktadır. Bu
firmadan 4 koli yumurta alan bir müşteri, her bir koliden rassal olarak bir yumurta aldığında,
3 kırık yumurta ile karşılaşma olasılığı nedir?
Sorunun iki terimli dağılıma uyduğunu şuradan anlıyoruz: Rassal olarak seçilen
yumurtalar kırık mı değil mi? Diğer bir ifadeyle iki sonuçlu bir durum söz konusudur.
X değişkeni: Seçilen 4yumurtanın kırık olması
𝑋 = {0,1,2,3,4}
4 𝑦𝑢𝑚𝑢𝑟𝑡𝑎 𝑜𝑙𝑑𝑢ğ𝑢𝑛𝑑𝑎𝑛
𝑛=4
𝑝: 𝑦𝑢𝑚𝑢𝑟𝑡𝑎𝑙𝑎𝑟ı𝑛 𝑘ı𝑟ı𝑙𝑚𝑎 𝑜𝑙𝑎𝑠ı𝑙ığı
1 − 𝑝 : 𝑦𝑢𝑚𝑢𝑟𝑡𝑎𝑙𝑎𝑟ı𝑛 𝑘ı𝑟ı𝑙𝑚𝑎𝑚𝑎 𝑜𝑙𝑎𝑠ı𝑙ığı
𝑝 = 0.05 1 − 𝑝 = 0.95
𝑃 𝑋=𝑥 =
𝑛!
𝑝 ! (1 − 𝑝)!!!
𝑥! 𝑛 − 𝑥 !
𝑃 𝑋=0 =
4!
(0.05)! (1 − 0.05)! = 0.814
0! 4 − 0 !
𝑃 𝑋=1 =
4!
(0.05)! (1 − 0.05)! = 0.171
1! 4 − 1 !
𝑃 𝑋=2 =
4!
(0.05)! (1 − 0.05)! = 0.020
2! 4 − 2 !
11 𝑃 𝑋=3 =
𝑃 𝑋=4 =
4!
0.05
3! 4 − 3 !
!
1 − 0.05
!
= 0.00047
4!
(0.05)! (1 − 0.05)! = 0.0000062
4! (4 − 4)!
Seçilen 4 yumurtanın hiç kırık olmama ihtimali % 81,4 olurken; seçilen 4 yumurtanın
sadece 1’inin kırık olma olasılığı da %17,1’dir.
Poisson Olasılık Dağılımı
Mesafe ve zaman ölçümü içeren sorunlarda kullanılmaktadır. Örneğin, otobanın belirli
mesafeleri arasında araçların arıza yapma olasılığı veya bir saat içerisinde bir dükkâna belirli
sayıda müşteri gelme olasılıklarının hesaplanmasında kullanılır.
Temel Varsayımlar
(a) Belirli zaman veya mesafe aralığında meydana gelen olayların birbirinden
bağımsız olduğu kabul edilir.
(b) Belirli aralıkta meydana gelen olayların ortalama dağılımı, aralıklar için hep eşittir.
𝑒 !! 𝜆!
𝑃 𝑋=𝑥 =
𝑥!
𝑒 = 2.718
λ: Belirli aralıkta meydana gelen ortalama olay sayısı
Örnek: Serdivan kavşağında yılın ilk altı ayında ortalama 5 kaza meydana geldiyse,
önümüzdeki altı ayda 2 kaza olma olasılığı nedir?
X: Serdivan kavşağında meydana gelen kaza sayısı
𝜆=5
𝑃 𝑋 = 2 =?
𝑃 𝑋=2 =
𝑒 !! (5)!
= 0.084
2!
Sonraki üç ay içerisinde 3 kaza meydana gelme olasılığı nedir?
Bu durumda ortalama kaza sayısı 2,5 olacaktır:
𝜆 = 2,5
𝑃 𝑋 = 3 =?
𝑃 𝑋=3 =
𝑒 !!.! (2.5)!
= 0.213
3!
Sonraki üç ayda 3 kaza meydana gelme olasılığı % 21.3’tür.
12 D – 2 - SÜREKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI
Belirli bir sayı aralığında olası bütün değerleri alabilen değişkenlerdir. Örneğin,
ücretler, maliyetler, ağırlıklar gibi.
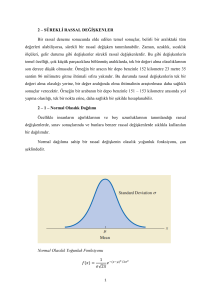
Sürekli rassal değişkenlerin dağılım formunun normal olduğunu kabul ediyoruz.
Çan eğrisi şeklindeki olasılık yoğunluk fonksiyonunun altında kalan alanın sayısal
değeri “1”dir. Bunun bir diğer anlamı, X rassal değişkinine ait bütün gözlem değerleri, bu çan
eğrisinin altında yer almaktadır. Her hangi bir rassal değişkenin belirli aralıktaki olasılığının
bulunabilmesi için standart normal dağılıma dönüştürmesi yapılır. Dönüştürme işlemi,
aşağıdaki formül aracılığı ile yapılır:
𝑍=
𝑋−𝜇
𝜎
Elde edilen standart normal dağılım değeri (Z değeri) ile standart normal dağılım
tablosundaki olasılık değeri bulunur.
Örnek: Bir tarantula türü olan Mollicoma örümceklerinin yetişkin erkeklerinin boyu
18.14 mm ortalama ve 1.76 mm standart sapma ile normal dağılım göstermektedir.
a) Rassal olarak seçilen yetişkin erkek Mollicoma örümceğinin uzunluğunun 16.34
mm’den kısa olma olasılığı nedir?
b) Bu örümceklerin yüzde kaçının uzunluğu 17.00 mm ile 19.00 mm aralığındadır.
c) Örümceklerin en uzun olan % 10’u, kaç mm’den daha uzundur?
Çözüm – a: Örümceklerin uzunluklarının normal dağılım gösterdiği bilgisi
verilmiştir. Belirli uzunluk değerleri için olasılık (veya sıklık) değerlerini bulabilmek için,
13 standart normal dağılıma dönüştürme yapılmalıdır. Bu dönüştürme işleminde kullanılacak
veriler, aşağıdaki gibidir:
𝑋 𝑟𝑎𝑠𝑠𝑎𝑙 𝑑𝑒ğ𝑖ş𝑘𝑒𝑛𝑖: Ö𝑟ü𝑚𝑐𝑒𝑘𝑙𝑒𝑟𝑖𝑛 𝑢𝑧𝑢𝑛𝑙𝑢𝑘𝑙𝑎𝑟ı 𝑚𝑚
𝜇 = 18.14 𝑚𝑚
𝜎 = 1.76 𝑚𝑚
𝑃 𝑋 ≤ 16.34 𝑚𝑚 =?
𝑍=
𝑋 − 𝜇 16.34 − 18.14
=
𝜎
1.76
𝑍 = −1.02
Negatif standart normal dağılım tablosunda bu Z değerine denk gelen alan sayısı
0.1539’dur. Bunun anlamı, standart normal dağılıma sahip rassal değişkenin değeri eksi
sonsuzdan – 1.02 değerine kadar geldiğinde taradığı alanın sayısal değeri 0.1539’dur.
𝑃 𝑍 ≤ −1.02 = 0.1539
Normal dağılıma sahip rassal değişkenin sayısal değerleri ile bu dönüştürmeyi
yaptığımız için, X rassal değişkeninin 16.34 mm’den daha düşük olma olasılığı da aynı değere
eşit olacaktır:
𝑃 𝑋 ≤ 16.34 𝑚𝑚 = 𝑃 𝑍 ≤ −1.02
14 𝑃 𝑋 ≤ 16.34 𝑚𝑚 = 0.1539
Mollicoma türü örümceklerin yetişkin erkeklerinin % 15.39’unun uzunluğu, 16.34 mm
ve daha kısadır. Diğer bir ifadeyle, Mollicoma türü örümceklerden rassal olarak seçilen
yetişkin bir erkeğin boy uzunluğunun 16.34 mm’den daha kısa olma olasılığı % 15.39’dur.
b) 𝑃 17.00 𝑚𝑚 ≤ 𝑋 ≤ 19.00 𝑚𝑚 =?
𝑋! = 17.00
𝑋! = 19.00
İlk önce 𝑋! değeri için dönüştürme yapalım:
𝑍! =
𝑋! − 𝜇 19.00 − 18.14
=
𝜎
1.76
𝑍! = 0,48
Pozitif standart normal dağılım tablosunda 0,48 için alanın sayısal değeri 0.6844’tür.
Bunun anlamı Z değişkeni eksi sonsuzdan gelip 0.48 sayısal değerine kadar taradığı alanın
sayısal değeri 0.6844’tür.
𝑃(𝑍! ≤ 0,48) = 0.6844
Şimdi 𝑋! için dönüştürme yapalım:
𝑍! =
𝑋! − 𝜇 17.00 − 18.14
=
𝜎
1.76
𝑍! = −0.64
Negatif tabloda – 0.64’e denk gelen alanın sayısal değerine baktığımızda 0.2611
değerini görürüz. Bunun anlamı, Z değişkeni eksi sonsuzdan gelip – 0.64 değerine kadar
taradığı alanın sayısal değeri 0.2611’dir.
𝑃(𝑍! ≤ −0.64) = 0.2611
Aradığımız olasılık, 𝑍! ve 𝑍! arasında kalan alanın sayısal değeridir:
𝑃 𝑍! ≤ 𝑍 ≤ 𝑍! =?
𝑃 −0.64 ≤ 𝑍 ≤ 0.48 = 𝑃(𝑍! ≤ 0,48) − 𝑃(𝑍! ≤ −0.64)
𝑃 −0.64 ≤ 𝑍 ≤ 0.48 = 0.6844 − 0.2611
𝑃 −0.64 ≤ 𝑍 ≤ 0.48 = 0.4233
15 𝑃 17.00 𝑚𝑚 ≤ 𝑋 ≤ 19.00 𝑚𝑚 = 𝑃 −0.64 ≤ 𝑍 ≤ 0.48
𝑃 17.00 𝑚𝑚 ≤ 𝑋 ≤ 19.00 𝑚𝑚 = 0.4233
Rassal olarak seçilen bir örümceğin uzunluğunun 17 ile 19 mm arasında olma olasılığı
% 42.33’tür.
c) 𝑃 𝑋 ≥? = 0.10
İstenilen X değerini bulabilmek için önce standart normal dağılım tablosunda
kendisinden sonra kalan alanın sayısal değeri 0.1000 olan Z değerini bulmalıyız. Pozitif Z
tablosunda 1.28 sayısal değerinin karşılığı 0.8997’dir. Bunun anlamı, eksi sonsuzdan gelip
1.28 sayısına kadar standart normal dağılıma sahip rassal değişkenin gözlem değerlerinin %
89.97’si geçilmiştir. Bu noktadan sonra kalan kısımda (yaklaşık olarak) gözlem değerlerinin
% 10’u bulunmaktadır:
𝑃 𝑍 ≥ 1.28 = 0.10
Şimdi Z değerini X değerine dönüştürelim:
𝑍=
𝑋−𝜇
𝜎
16 1.28 =
𝑋 − 18.14
1.76
1.28 1.76 = 𝑋 − 18.14
𝑋 = 20.39 𝑚𝑚
Bu tür örümceklerin % 10’u, 20.39 mm’den daha uzundur.
E - ÖRNEKLEM ORTALAMALARININ DAĞILIMI
Anakütlenin gözlemlenebildiği bir durumda hesaplanacak olan parametrelerin, örneğin
ortalama ve standart sapma, sadece tek bir değeri olacaktır. Örneğin bir ampul üreticisi bir
firma, bir üretim süreci sonucunda 1 milyon ampul üretiyor ve bunların tamamının saat olarak
ömrünü ölçebiliyorsa, ampulleri için ortalama bir ömür (saat) belirleyecektir ve bu değer, tek
bir sayısal değer (parametre) olacaktır.
Ancak gerçek hayatta anakütlenin tamamının gözlemlenmesi çoğu zaman mümkün
değildir. Bunun için anakütleden örneklem çekilecektir. 1 milyon ampul üreten bir firmanın
ampullerin ömrünü kontrol etmek için 100 veya 1000 ampulü alıp ölçüm yaptığını düşünelim.
Alınan örneklemin kendine özgü bir ortalama değeri (istatistik) olacaktır. Ancak dikkat
edilmesi gereken nokta, çekilen tek bir örneklemden elde edilen ortalama değeri, 1 milyon
gözlem sayısına sahip anakütleden 100 veya 1000 elemanlı çekilebilecek örneklemlerden
17 sadece biridir. Dolayısıyla 1 milyonun 100’lü kombinasyonu sonucunda kaç tane farklı
örneklem elde edilebilecekse, o kadar farklı örneklem ortalamaları elde edilecektir.
Merkezi Limit Teoremi
(1) Ortalaması 𝜇 ve standart sapması 𝜎 olan (dağılımı normal olsun veya olmasın) bir
anakütleden çekilen örneklemin gözlem sayısı 30’dan büyükse (𝑛 ≥ 30), elde
edilebilecek örneklemlerin ortalamalarının dağılımı, beklenen değeri (ortalaması)
𝜇 ve standart sapması 𝜎
𝑛 ile normal dağılım gösterecektir.
(2) Ortalaması 𝜇 ve standart sapması 𝜎 olan ve normal dağılım gösteren bir
anakütleden çekilen örneklemin gözlem sayısı 30’dan küçükse (𝑛 < 30), elde
edilebilecek örneklemlerin ortalamalarının dağılımı, beklenen değeri (ortalaması)
𝜇 ve standart sapması 𝜎
𝑛 ile normal dağılım gösterecektir.
Dikkat edilirse bu iki koşul altında örneklem ortalamalarının ortalaması (𝝁𝑿 ) ile
anakütle ortalaması (𝝁) birbirine eşit olmaktadır. Mümkün olan bütün örneklemlerin
ortalamaları hesaplandığı için örneklem ortalamalarının dağılımı da ayrı bir anakütle
olacaktır. Bu anakütlenin ortalaması ve standart sapması, şu şekilde sembolize edilecektir:
𝜇! : Ö𝑟𝑛𝑒𝑘𝑙𝑒𝑚 𝑜𝑟𝑡𝑎𝑙𝑎𝑚𝑎𝑙𝑎𝑟ı𝑛ı𝑛 𝑜𝑟𝑡𝑎𝑙𝑎𝑚𝑎𝑠ı
𝜎! : Ö𝑟𝑛𝑒𝑘𝑙𝑒𝑚 𝑜𝑟𝑡𝑎𝑙𝑎𝑚𝑎𝑙𝑎𝑟ı𝑛ı𝑛 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑡 𝑠𝑎𝑝𝑚𝑎𝑠ı
Bu bilgiler ışığında, örneklem ortalamalarının dağılımına dair olasılıkları bulabilmek
için standart normal dağılım dönüştürmesi, şu şekilde yapılacaktır:
𝑍=
𝑋 − 𝜇! 𝑋 − 𝜇!
=
𝜎!
𝜎 𝑛
Örnek: Bir emlak dergisinin yapmış olduğu araştırmada Bodrum’daki evlerin
ortalama metrekare fiyatı 18000 TL bulunmuştur. Anakütle, standart sapması 4000 TL ile
normal dağılım göstermektedir.
a) Anakütleden çekilen bir evin metrekare fiyatının 23750 TL’den büyük olma
olasılığı nedir?
Soruda verilenler:
𝜇 = 18.000 𝑇𝐿
𝜎 = 4.000 𝑇𝐿
𝑃 𝑋 ≥ 23.750 𝑇𝐿 =?
18 Normal dağılama sahip bu rassal değişkenin değerlerini, standart normal dağılıma
dönüştürelim:
𝑍=
𝑋 − 𝜇 23.750 − 18.000
=
𝜎
4.000
𝑍 = 1.43
Pozitif Z tablosunda bu değerin karşısında 0.9236 yazmaktadır. Bunun anlamı, Z
rassal değişkeni eksi sonsuzdan gelip 1.43 sayısına kadar taradığı alanın sayısal değeri
0.9236’dır.
𝑃 𝑍 ≤ 1.43 = 0.9236
Ancak biz, bu değerden daha büyük olma olasılığını arıyoruz:
𝑃 𝑍 ≥ 1.43 = 1 − 𝑃 𝑍 ≤ 1.43
𝑃 𝑍 ≥ 1.43 = 1 − 0.9236
𝑃 𝑍 ≥ 1.43 = 0.0764
Standart normal dağılıma sahip rassal değişkenin 1.43 değerini aşma olasılığı ile
normal dağılıma sahip rassal değişkenin 23.750 TL değerini aşma olasılığı eşittir:
𝑃 𝑋 ≥ 23.750 𝑇𝐿 = 𝑃 𝑍 ≥ 1.43
𝑃 𝑋 ≥ 23.750 𝑇𝐿 = 0.0764
Bodrum’da rassal olarak seçilen bir evin metrekare fiyatının 23.750 TL’den daha fazla
olma olasılığı % 7,64’tür.
19 b)Anakütleden çekilen 32 gözlemli bir örneklemin ortalamasının 23750 TL’den
yüksek olma olasılığı kaçtır?
Örneklem olduğu için dönüştürme işlemi ve dağılımın parametreleri değişecektir:
𝑛 = 32
𝜇 = 𝜇! = 18.000 𝑇𝐿
𝜎! = 𝜎
𝑛 = 4.000 32 = 707,96
𝑃 𝑋 ≥ 23.750 𝑇𝐿 =?
Bu sorunun cevabını bulabilmek için verilenleri Z değişkenine dönüştürelim:
𝑍=
𝑋 − 𝜇! 𝑋 − 𝜇! 23.750 − 18000
=
=
𝜎!
707,96
𝜎 𝑛
𝑍 = 8,12
Pozitif Z tablosunda en büyük Z değeri 3,50’dir. Standart normal dağılıma sahip rassal
değişkenin bu değeri aşma olasılığı oldukça düşüktür.
𝑃 𝑋 ≥ 23.750 𝑇𝐿 = 𝑃 𝑍 ≥ 8,12 = 0,0001
Dikkat edilirse bir anakütleden tek bir gözlem çekmek ile belirli bir büyüklükte
örneklem çekip ortalamasının olasılığını bulmak, oldukça farklı olasılık değerleri vermektedir.
20