15
1
Çembersel Hareket
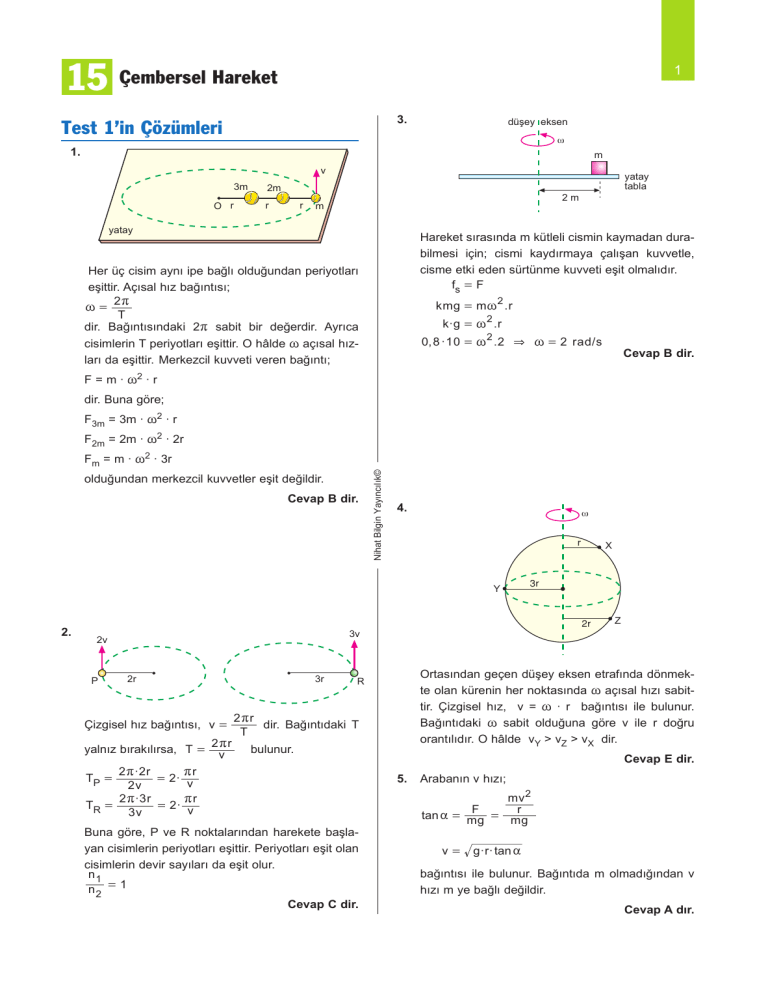
3.
Test 1’in Çözümleri
düşey eksen
ω
1.
m
v
3m
O r
yatay
tabla
2m
r
r
2m
m
yatay
Her üç cisim aynı ipe bağlı olduğundan periyotları
eşittir. Açısal hız bağıntısı;
2r
~=
T
dir. Bağıntısındaki 2r sabit bir değerdir. Ayrıca
cisimlerin T periyotları eşittir. O hâlde ~ açısal hızları da eşittir. Merkezcil kuvveti veren bağıntı;
F = m · ~2 · r
dir. Buna göre;
F3m = 3m · ~2 · r
F2m = 2m · ~2 · 2r
Fm = m · ~2 · 3r
olduğundan merkezcil kuvvetler eşit değildir.
Cevap B dir.
kmg = m ~ 2 . r
k·g = ~2 .r
0, 8 · 10 = ~ 2 . 2
Nihat Bilgin Yayıncılık©
Hareket sırasında m kütleli cismin kaymadan durabilmesi için; cismi kaydırmaya çalışan kuvvetle,
cisme etki eden sürtünme kuvveti eşit olmalıdır.
fs = F
& ~ = 2 rad / s
4.
ω
r
Y
2.
3r
Z
3v
2v
2r
3r
Çizgisel hız bağıntısı, v =
yalnız bırakılırsa, T =
X
2r
P
Cevap B dir.
2r r
v
R
2r r
dir. Bağıntıdaki T
T
bulunur.
2r·2r
rr
TP =
= 2· v
2v
rr
2r·3r
= 2· v
TR =
3v
Buna göre, P ve R noktalarından harekete başlayan cisimlerin periyotları eşittir. Periyotları eşit olan
cisimlerin devir sayıları da eşit olur.
n1
n2 = 1
Cevap C dir.
Ortasından geçen düşey eksen etrafında dönmekte olan kürenin her noktasında ~ açısal hızı sabittir. Çizgisel hız, v = ~ · r bağıntısı ile bulunur.
Bağıntıdaki ~ sabit olduğuna göre v ile r doğru
orantılıdır. O hâlde vY > vZ > vX dir.
Cevap E dir.
5. Arabanın v hızı;
mv 2
F
r
tan a = mg = mg
v=
g · r · tan a
bağıntısı ile bulunur. Bağıntıda m olmadığından v
hızı m ye bağlı değildir.
Cevap A dır.
ÇEMBERSEL HAREKET
6. K cismi r yarıçaplı yörüngede,
L cismi ise 3r
yarıçaplı yörüngede aynı çizgisel hızla dolanmaktadır. K cismi
3
devir yaptı2
ğında L cismi ise
1
bu süre içinde
2
devir yapar.
3r
/
2/
O1
r
ω2
ω1
O2
2m
v
v
K
L
v
m
O
v
Açısal hız ile çizgisel hız arasındaki ilişki ~ = r ile
verilir.
~1 = ~2
v1
v2
v
=
& v 1 = 1 bulunur .
,
2,
2
2
Cevap D dir.
L cismine göre K cisminin hızı sorulmuş. L vektörünü aynen alıp K vektörünü ters çevirip işlem yaptığımızda bileşke sıfır çıkar.
Cevap E dir.
7. Çembersel
hareket
yapan bir cisme etki
eden merkezcil kuvvet
vektörünün yönü dönme
sırasında sürekli değişir.
Bu nedenle cismin hareketi sırasında F sabit
kalmaz.
8.
Nihat Bilgin Yayıncılık©
2
m
9.
r
O
α
F
r
K
N
v
F
r
v
m
L
h
mg
Cisim çembersel hareket yaparken hız vektörünün
yönü de sürekli değişir. P = m v bağıntısına göre,
v değişeceğinden P de değişir.
Açısal hız vektörü ile açısal momentum vektörü
aynı yönde olup, yönleri sağ el kuralı ile bulunur.
Sağ elin dört parmağı dönme yönünde büküldüğünde, yana açılan baş parmak açısal momentum
vektörünün yönünü gösterir. Cisim yatay düzlem üzerinde çembersel hareket yaparken açısal
momentum sayfa düzlemine dik olup yönü bize
doğrudur. Hareket sırasında yön değişmemektedir.
Açısal momentumun büyüklüğü ise L = mvr bağıntısıyla bulunur. m, v, r değerleri değişmediğinden L
değişmez.
Cevap B dir.
Yerden h yükseklikteki K noktasından serbest bırakılan m kütleli cisim L noktasından v büyüklüğündeki hızla geçer. L noktasında cisme etki eden kuvvetler;
v2
N = mg + m r
dir. K ve L konumunda cismin sahip olduğu enerjilerin eşitliğinden;
1
mgh =
mv2 & v2 = 2gh
2
yazabiliriz. v2 ile h = r – r cosa değerlerini yerine
yazarsak;
2 g ( r - r · cos a )
r
N = mg + m
N = mg + 2 mg ( 1 - cos a )
bulunur. Buna göre, N tepki kuvvetinin büyüklüğü,
verilenlerden yalnızca r ye bağlı değildir.
Cevap E dir.
3
ÇEMBERSEL HAREKET
10.
12.
B
N
v1
F
F
r
O
N
α
α
mg
mg
v2
Eğimli yolda otomobilin mg ağırlığı ile yüzeyin N
tepki kuvvetinin bileşkesi olan F , merkezcil ivmeyi
kazandıran kuvvettir. Şekildeki dik üçgenden;
F
tan a = mg ve F = ma olduğundan;
ma = mg·tana
a = g·tan45° = g
A
B noktasında cisimle ray arasındaki tepki kuvveti
sıfır olduğuna göre, bu noktada merkezcil kuvvet ile
cismin ağırlığı birbirine büyüklük olarak eşittir.
mv 12
r = mg
Cevap E dir.
v 12 = gr
A ve B noktalarındaki enerji eşitliğinden;
1
mv 12 + mg · h
2
5
1
E K ( A ) = mgr + mg · 2 r = mgr
2
2
EK ( A ) =
Cevap D dır.
Nihat Bilgin Yayıncılık©
13.
v1
3m
2/
O2
O1
3/
11.
ω
2m
yatay
O
m
Yay sabiti k olan bir yaya F kuvveti uygulandığında yay x kadar açılır. Kuvvet ile uzama miktarı arasında, F = kx bağıntısı vardır. Çembersel hareket
yapan bir sistemde merkezcil kuvvet;
F=m
4r2 ·r
T2
bağıntısı ile bulunur. Hareketin periyodu yarıya
indirilirse kuvvet 4 kat artar. Periyot T iken yaydaki
1
T
uzama miktarı x ise periyot
olduğunda yay2
2
daki uzama 2x olur. Yayın ilk boyu 2x olduğundan
son boyu 4x olur.
Cevap C dir.
2r·2,
T
2r·3,
v2 =
T
v1
~1 = r =
1
v2
~2 = r =
2
v1 =
v2
r,
T
r·,
= 6·
T
=4
4r·,
r
=2
T2,
T
6r·,
r
=2
T3,
T
4r·, 2
(
)
v 12
mr2 ,
T
F1 = 3 m · r = 3 m
= 24
2,
1
T2
6
·
r
,
(
)2
v 22
mr2 ,
T
F2 = 2 m · r = 2 m
= 24
3,
2
T2
Buna göre, her iki cisim için eşit olan nicelik açısal
hız ve merkezcil kuvvettir.
Cevap E dir.
4
ÇEMBERSEL HAREKET
16.
14.
A
30°
/
2
A
/
m
B
60°
20 m
T
B
r
/
mgcos60°
v
5m
yatay
mg
v2
m r = T - mg cos 60°
g,
1
= T - mg ·
m
,
2
3
T = mg
2
Cisim A noktasında iken yalnızca potansiyel enerjisi vardır. Cisim B den geçerken hem kinetik, hem
de potansiyel enerjisi vardır. Enerji korunumundan;
1
mg · h = mv 2 + mg ·2 r
2
1
10·20 = v 2 + 10·10
2
1
100 = v 2
2
Cevap B dir.
v = 10 2 m / s
Cevap D dir.
Nihat Bilgin Yayıncılık©
m kütleli cismin, A noktasındaki potansiyel enerjisi
B noktasında kinetik enerjiye dönüşür.
,
1
mg = mv 2 & v 2 = g ,
2
2
İpteki T gerilme kuvveti ile mg ağırlığının ip doğrultusundaki bileşeni merkezcil kuvveti oluşturur.
17.
Y
O
ip
yatay
60°
m
X
15.
v
6ω
P
M
r
ω
N
L
r
3r
r
K
3ω
N dişlisi gösterilen yönde ~ açısal hızıyla dönüyorsa L dişlisi, dolayısıyla K dişlisi 3~ açısal hızıyla döner. K dişlisi 3~ açısal hızıyla dönerken M dişlisi 6~ açısal hızıyla döner. Frekans birim zaman
içindeki devir sayısıdır. Birim zaman içindeki devir
sayısı en küçük olan N dişlisidir.
Cevap B dir.
X noktasında ipteki gerilme kuvveti ile mg ağırlığının bileşkesi merkezcil kuvveti oluşturur. Buna
göre;
v2
m r = T - mg cos 60 ° .................( 1 )
Cisim Y noktasından geçerken ipteki gerilme kuvveti Tl olsun. Y noktasındaki merkezcil kuvvet, ipteki gerilme kuvveti ile mg ağırlığının toplamıdır.
v2
m r = Tl + mg ........................... ( 2 )
(1) ve (2) bağıntılarının eşitliğini kullanırsak;
T - mg cos 60 ° = Tl + mg
5
1
mg - mg · = Tl + mg
2
2
Tl = mg olur .
Cevap B dir.
ÇEMBERSEL HAREKET
18.
düşey
ω
2r
r
θ
yatay
m1 kütleli cismin çizgisel hızı v ise m2 kütleli cismin
çizgisel hızı 2v olur. Cisimlerin açısal hızları ise;
v1
v
~1 = r = r
1
v2
2v
v
~2 = r =
= r
2r
2
bulunur. Cisimlere etki eden merkezcil kuvvetler;
v 12
v2
F1 = m · r = m · r
1
v 22
4v2
mv 2
= 2· r
F2 = m · r = m ·
2r
2
Buna göre, her iki cisim için açısal hızlar eşit, çizgisel hız ile merkezcil kuvvet değerleri farklıdır.
Cevap C dir.
Nihat Bilgin Yayıncılık©
m1
θ
O
m2
5
6
ÇEMBERSEL HAREKET
Test 2’nin Çözümleri
1.
r1
2m
Dv =
v2
Cisimlerin periyotları eşit olduğundan, açısal hızları
eşit demektir. Açısal hızları eşit olduğuna göre, çizgisel hızları yarıçapla doğru orantılıdır. v2 = 2v1 ise,
r2 = 2r1 dir. Verilen değerleri merkezcil kuvvet bağıntısında yerine yazalım;
F1
F2
F1
F2
=
=
m 1 · v 21
r1
m 2 · v 22
r2
=
m · v 21
r1
2 m · 4 v 21
v 21 + v 22 = 10 2 m/s
∆t = 0,5 s
değerleri yerine yazılırsa;
a ort =
10 2
= 20 2 m/s2 bulunur.
0, 5
Yanıt D dir.
m · v 21
r1
2 m · ( 2 v 1) 2
2 r1
=
a ort =
1
4
Nihat Bilgin Yayıncılık©
m
r2
v2 - v1
Dv
=
Dt
Dt
bağıntısı ile bulunur. v 2 vektörü aynen alınırken,
v 1 vektörü ters çevrilerek vektörel işlem yapılır. Sayısal değer olarak v1 = v2 = 10 m/s dir.
v1
Cisim t = 0 anında şekildeki yörüngenin K noktasında ise, 0,5 s sonra L noktasından geçer. Ortalama
ivme;
bulunur.
2 r1
Yanıt E dir.
3.
L
s–1
2. Frekansı 0,5
olduğuna göre, periyodu T = 2 s
olur. Yani cisim, 2 s de 360° yi dolanmaktadır. O hâlde 0,5 s de 90° lik bir dönüş yapar.
K
v1
r=1m
O
Hareket yatay düzlemde olduğundan, bütün noktalarda ipi geren kuvvet eşit olup, merkezcil kuvvet kadardır.
TK = TL =
v2
∆v
v2
– v1
K
R
L
v
2 · 32
mv 2
r = 1 = 18 N olur.
Yanıt C dir.
7
ÇEMBERSEL HAREKET
4.
6.
r
N
T=2 mg
v
mg
mg
Uçak r yarıçaplı çembersel yörüngede dolanırken
en fazla 5g lik çekim ivmesine dayanabilmektedir.
Uçak yörüngenin en alt noktasından geçerken pilota
uygulanan tepki kuvveti N olsun. Buradan;
N – mg = Fmerkezcil
N – mg =
5mg =
Cisim yörüngenin en alt noktasından geçerken, ipteki T gerilme kuvveti, merkezcil kuvvetle ağırlığın toplamı kadar olur.
mv 2
r = 2mg
T = mg +
olduğundan, yalnızca merkezcil kuvvet F = mg kadardır.
F=
mv 2
r = mg
v2 = gr = 10 . 0,9 = 9
v2
5g = r + g
4g =
v = 3 m/s
bulunur.
Yanıt C dir.
5.
v
Nihat Bilgin Yayıncılık©
mv 2
r
mv 2
r + mg
( 200 ) 2
r
r = 1000 m bulunur.
Yanıt E dir.
7. Otomobilin güvenle
dönüş
yapabilmesi
için tekerlek ve yol
arasındaki sürtünme
kuvveti merkezcil kuvvete eşit olmalıdır.
mg
r=0,4 m
Kova şekildeki gibi düşey çembersel yörüngede dolanırken suyun dökülmemesi için, merkezcil kuvvetin ağırlıktan büyük veya eşit olması gerekir. Yani;
v
r
fs= k . N
Arabanın güvenle dönebilmesi için;
fs = Fmerkezcil
mv 2
r
F ≥ mg
k·N =
olmalıdır. Hızın en küçük değeri, istendiğinden
koşulu sağlanmalıdır.
F = mg alınarak;
v=
kgr
v=
0, 4 · 10 · 100
v = 20 m/s
Aracın bu yolu güvenle dönebilmesi için, hızı en fazla 20 m/s olmalıdır.
mv
r
2
= mg
v2 = gr = 10 · 0,4 = 4
v = 2 m/s
bulunur.
Yanıt D dir.
Yanıt E dir.
8
ÇEMBERSEL HAREKET
8.
10.
N
K
zincir
P
L
m
r
X
F
Y
a
mg
Z
3r
2r
M
zincir
Kasnakların dönme sayıları ile açısal hızları doğru
orantılıdır. X ve Y kasnakları eş merkezli olduğundan hem dönme sayıları hem de açısal hızları eşittir
(~K = ~L). X kasnağı 2 devir yaptığında Z kasnağı 1
devir yapar. Bu nedenle, ~L = 2~M dir.
Aracın güvenli biçimde dönebilmesi için mg ağırlık kuvveti ile yolun N tepki kuvvetinin bileşkesi
merkezcil kuvvete eşit olmalıdır.
F
tana = mg
Çizgisel hız ile açısal hız arasında v = ~r ilişkisi olduğundan;
vK = ~K · 3r = 2~ · 3r = 6~r
mv 2
r
v2
tana = mg = rg
vL = ~L · r = 2~ · r = 2~r
vM = ~M · 2r = ~ · 2r = 2~r
vK > vL = vM bulunur.
20 2
2
tana =
=
5
100 · 10
bulunur.
Yanıt B dir.
Nihat Bilgin Yayıncılık©
Yanıt B dir.
9. Düşey silindirin yan yüzeyinde dolanan cismin düşmemesi
için;
fs
fs ≥ mg
kN ≥ mg
olmalıdır. Bağıntıdaki N merkezcil kuvvet kadardır. Bu nedenle;
k·
mg
gr
≥
k
olmalıdır. Cismin düşmeden dolanabileceği en küçük hız için;
v2
11.C cismine etkiyen kuvvetler şekildeki gibidir. Cismin
düşmemesi için, fs sürtünme
kuvveti, mg ağırlığından büyük ya da en az eşit olmalıdır. O hâlde;
g·r
10 · 2
=
≥
k
0, 2
= 100
v = 10 m/s
bulunur.
Yanıt A dır.
~
r
fs
C
mg
fs = mg
kN = mg
yazılabilir. Bağıntıdaki N, merkezcil kuvvet kadardır.
Bu nedenle açısal hız;
k·
≥ mg
v2
v2
mv
r
2
~
mv 2
r = mg
gr
v2 =
k
gr
~2 · r2 =
k
~=
~=
g
k ·r
10
= 5 rad/s bulunur.
0, 2 · 2
Yanıt E dir.
9
ÇEMBERSEL HAREKET
14.
12.
N
~
fs
L
yatay
tabla
r
r
1m
K
v
mg
m
Yatay tablada cisme etkiyen kuvvetler şekilde gösterilmiştir. Bunlardan mg ile N birbirini dengeler. Cismin
tabla üzerinde kaymaya başladığı an, sürtünme kuvvetinin, merkezcil kuvvetle eşit olduğu andır.
mv 2
r
fs = Fmerkezcil =
kN =
N yerine mg, v2 yerine de
mv 2
r
Düzgün çembersel hareket yapan cismin periyodu
6 saniyedir. Cisim şekildeki K noktasından geçtikten 12 saniye sonra yine K noktasında olur. K noktasından geçtikten 3 saniye sonra ise L noktasında
olur. Bu durumda cismin yer değiştirmesi 2r dir.
Yanıt B dir.
~2r2
değerlerini yazarsak;
m~2r
kmg =
~=
~ = 2 rad/s bulunur.
kg
r =
0, 4 · 10
1
15.
v
v
120°
Nihat Bilgin Yayıncılık©
Yanıt B dir.
13.
Talt = 3mg
Cisim 4 saniyede 120° açı taradığına göre 360°
yi 12 saniyede tarar. Bu da, cismin periyodu 12
saniye demektir. Cismin periyodu 12 saniye ise fre1 –1
kansı
s
olur.
12
Yantı E dir.
v
mg
16.
Kova yörüngenin en alt noktasından geçerken kovaya uygulanan kuvvetler şekilde gösterilmiştir.
Talt = Fmerkezcil + mg
3mg = Fmerkezcil + mg
v = 3 m/s
r = 100 cm
Fmerkezcil = 2mg
Newton’un ikinci hareket yasası olan F = ma bağıntısına göre merkezcil ivme;
Fmerkezcil
a=
m
v2
a= r
bağıntısıyla bulunur. Buradan;
a=
2 mg
a = m = 2g
bulunur .
Yanıt B dir.
m
Düzgün çembersel hareket yapan cismin merkezcil
ivmesi;
32
= 9 m/s2
1
bulunur.
Yanıt E dir.
10
ÇEMBERSEL HAREKET
3.
Test 3’ün Çözümleri
y
ω
r = 0,5 m
r = 0,5 m
1.
K
Fs
Fs
3
O
h
m = 1 kg
r
m = 1 kg
Halkaların çembersel hareket yapabilmesi için merkezcil kuvvete ihtiyaç vardır. Bu merkezcil kuvveti
sürtünme kuvveti sağlar. Çubuğun maksimum frekansı;
Fs = m · ~2 · r
v 21
m r = T1 – mg
Fs = m · 4r2 · f2 · r
5 = 1 · 4 · 10 · f2 · 0,5
v 22
m r = T2
f=
2
T1
v1
1
mg
1 –1
s
bulunur.
2
Yanıt B dir.
m r = T3 + mg
ifadeleri kullanılarak T1, T2 ve T3 tepki kuvvetleri bulunur.
Ayrıca cismin hızını bulmak için;
mgh =
1
mv2
2
v2 = 2gh
ifadesi kullanılabilir.
Nihat Bilgin Yayıncılık©
v 23
4.
ω
Yanıt D dir.
T
2.
m
v
O
v2
r
m
r
mg
m1
45°
m2g
m1 kütlesinin çembersel hareket yapabilmesi için
v2
r kadar merkezcil kuvvete ihtiyaç vardır. Bu
merkezcil kuvveti m2 cisminin ağırlığı sağlar.
m1
2
v
m2g = m1 r
m2 =
m1 v
rg
Cisme uygulanan tepki kuvveti ile ağırlığın bileşkesi gerekli merkezcil kuvveti oluşturur. Cismin çizgisel
hızı;
v2
m r
tan45° = mg
v2
tan45° = rg
1=
2
Yanıt B dir.
v=
v2
0, 2 · 10
2 m/s bulunur.
Yanıt A dır.
11
ÇEMBERSEL HAREKET
5.
7.
ω = 4 rad/s
v
K
a
r=1m
Fs
A
O
r
Merkezcil ivmenin yönü, adından da anlaşıldığı gibi
daima merkeze doğrudur. Merkezcil ivmenin büyüklüğü;
4r2
a=
a = 4 · 32 ·
m/s2
a=4
·
f2
·r
1
·1
32
bulunur.
K cisminin kaymadan durabilmesi için gerekli merkezcil kuvveti sürtünme kuvveti sağlamalıdır. r yarıçapı;
k · mg = m~2 · r
0,32 · 10 = 42 · r
r = 0,2 m
r = 20 cm bulunur.
Yanıt C dir.
Nihat Bilgin Yayıncılık©
6.
düşey
FsX
8.
O
ω
N
T
Şekil I
37°
FsY
O
X
Yanıt D dir.
Y
mg = 10 N
O
T
Şekil II
Fs H m~2r koşulu sağlanırsa cisimler hareketsiz kalır. X cismi için;
kmg H m . 4r2T2 · r
0,2 · 10 H 4 · 32 · 12 · 0,5
2 H 18 olur.
37°
Demek ki X cismi dışarı doğru hareket eder.
Y cismi için;
kg H 4r2T2r
0,2 · 10 H 4 ·
32
·
12
mg.sin 37° = 6 N
· 0,1
Cisme etki eden kuvvetler şekilde gösterilmiştir. Bu
kuvvetlerin bileşkesi merkezcil kuvveti oluşturur. Bu
durumda ip doğrultusundaki kuvvetler Şekil II deki
gibi olur. Merkezcil kuvvetin ip doğrultusundaki bileşeni;
m~2 · r · Cos37° = T – mg Sin37°
2 H 3,6 olur.
Y cismi de dışarı doğru hareket eder.
Yanıt D dir.
1 · 5 · 0,8 = T – 6
T = 10 N bulunur.
Yanıt E dir.
12
ÇEMBERSEL HAREKET
9.
11.Düşey düzlemde çembersel hareket yapan cismin
en üst noktadan geçerken hızının en küçük olabilmesi için ipteki gerilme kuvveti sıfır olmalıdır. Bu durumda merkezcil kuvveti sadece cismin ağırlığı sağlar. Cismin ağırlığını merkezcil kuvvete eşitlersek;
düşey
ω
P
r
r
r
R
r
O
S
j2
mg = m r
~2r
Merkezcil ivme a =
bağıntısından bulunur. P, R,
S noktalarının açısal hızları eşit olduğu için, ivme
sadece dönme yarıçapına bağlıdır. Bu durumda yarıçapı büyük olan noktanın merkezcil ivmesi büyüktür. Buna göre, aP > aR = aS bulunur.
j=
gr bulunur.
Buna göre hızın en küçük değerinin bulunabilmesi
için yer çekimi ivmesi ve ipin uzunluğu (dönme yarıçapı) bilinmelidir.
Yanıt C dir.
10.
Nihat Bilgin Yayıncılık©
Yanıt C dir.
ω
37°
Fm
T
m2
12.
v2
v1
2r
3r
m1g
O
m1 kütlesinin ağırlığı ipte bir gerilme kuvveti oluşturur. Bu gerilme kuvvetinin yatay bileşeni de merkezcil kuvveti oluşturur. Buna göre, m2 kütlesine uygulanan merkezcil kuvvet;
F = mg · Sin37°
F = 1,5 · 10 · 0,6
F = 9 N bulunur.
Yanıt B dir.
r
v3
Dişliler birbirine bağlı olduğu için çizgisel hızları eşit
olmalıdır. Yani;
v1 = v2 = v3 olur.
Yanıt A dır.
13
ÇEMBERSEL HAREKET
13.
m
T
P
R
yatay
tabla
S
37°
r
m·
· r1 = 2m . ~2 · r2
r1 = 2r2
olur. Bu durumda dönme ekseni RS arasında olur.
PRATİK ÇÖZÜM
Bu tür sorularda dönme ekseni sistemin kütle merkezidir. Kütle merkezi RS arasında olduğundan dönme ekseni de RS arasındadır.
m
İpteki gerilme kuvveti ile cismin ağırlığının bileşkesi
gerekli merkezcil kuvveti oluşturur. Taralı üçgenden;
F
tan37° = mg
3
F
=
4
0, 1 · 10
3
F=
4
F = 0,75 N bulunur.
Fm
mg
F1 = F2
~2
=1m
T
Sürtünme kuvveti olmadığı için gerekli merkezcil
kuvveti, ipteki gerilme kuvveti sağlar. Cisimler aynı
iple birbirine bağlı olduğu için cisimlerin merkezcil
kuvvetleri eşit olmalıdır.
15.
2m
T
Yanıt B dir.
Nihat Bilgin Yayıncılık©
Yanıt D dir.
16.
M
K
v
v
N
r
r
2r
14.
K
3r
L
L
2r
T2 = 3 s
60°
~
2v
T1 = 2 s
360
= 180° açı tarar.
2
360
L cismi saniyede
= 120° açı tarar.
3
Hareket, şekildeki konumdan başladıktan 1 saniye
sonra K cismi L ye yetişir.
K cismi saniyede
Yanıt A dır.
K noktasının çizgisel hızı v olsun. Bu durumda M
noktasının çizgisel hızı 2v, N noktasının çizgisel hızı
da v olur. N noktasının çizgisel hızı L noktasının çizgisel hızına eşit olacağından L noktasının çizgisel
hızı da v olur. Buna göre;
v2
FK = m r
FL = 2m
FK
FL
=
3
2
v2
3r
bulunur.
Yanıt B dir.
14
ÇEMBERSEL HAREKET
17.
18.
N
m1
T
v
Fs
mg
T
r = 80 m
2
m2 v
r
Arabaya uygulanan kuvvetler şekilde gösterilmiştir.
Bu kuvvetlerin bileşkesi merkezcil kuvveti oluşturur.
Buna göre;
30 N
v2
m r = mg – N
1500
20 2
= 1500 · 10 – N
80
N = 7500 N bulunur.
m1 ve m2 kütleli cisimlere etki eden kuvvetler şekildeki gibidir.
Önce m2 kütlesine uygulanması gereken merkezcil
kuvveti bulalım.
v2
F=m r
Yanıt C dir.
4 · 10
3
F=3
Bu durumda ipteki gerilme kuvveti 50 N olmalıdır.
m1 kütleli cisim dengede kaldığına göre ipteki gerilme kuvveti sürtünme kuvvetine eşit olmalıdır.
T = Fs
50 = k · m1 · g
50 = 0,2 · m1 · 10
m1 = 25 kg
F = 40 N
Nihat Bilgin Yayıncılık©
bulunur .
bulunur.
Yanıt B dir.
ÇEMBERSEL HAREKET
me kuvveti ile ağırlığın bileşkesi sağlar. En üst noktadan geçerken ipteki gerilme kuvveti Tmin, en alt
noktadan geçerken ipteki gerilme kuvveti Tmax olur.
Merkezcil kuvvete F dersek;
Test 4’ün Çözümleri
1.
m
ip
X
α
· cosα
Y
α
mg · cosα
F = Tmax – mg
F = Tmin + mg
2F = Tmax + Tmin
bulunur. Bu durumda sadece merkezcil kuvvet bulunabilir.
Yanıt B dir.
mg
Cismin X noktasındaki potansiyel enerjisi Y noktasındaki kinetik enerjisine eşittir. Cismin Y noktasındaki hızı;
1
mv2
2
1
mg,·Cosa =
mv2
2
v2 = 2 g,·Cosa olur.
mgh =
İpteki gerilme kuvveti ile ağırlığının ip doğrultusundaki bileşeni merkezcil kuvveti oluşturur. Buradan;
v2
m r = T – mg·Cosa
2 g , Cos a
m
= T – mg·Cosa
,
T = 3 mg·Cosa
bulunur. Buna göre ipteki gerilme kuvveti ipin uzunluğuna bağlı değildir.
Yanıt C dir.
Nihat Bilgin Yayıncılık©
15
3.
ω
2.
Fs
v
mg
K
Tmin
mg
ip
4m
r
Tmax
v
mg
İpe bağlanmış cisim düşey düzlemde çembersel hareket yaparken gerekli merkezcil kuvveti, ipteki geril-
K cisminin düşmemesi için FS = mg olması gerekir.
kN = mg (Burada dik kuvvet merkezcil kuvvete eşittir.)
km~2r = mg
k · 52 · 4 = 10
k = 0,1 olur.
Yanıt A dır.
16
ÇEMBERSEL HAREKET
4.
6.
ω = 2 rad/s
ω
m = 100 gr
ip
1
2
50 cm
3
O
Çizgisel hız ile açısal hız arasındaki ilişki
v = ~ · r dır. 1, 2, 3 noktalarının açısal hızı aynı olduğundan bu noktaların çizgisel hızı dönme eksenine
olan uzaklıkla orantılıdır. Yani:
Merkezcil kuvvet ipteki gerilme kuvvetine eşit olduğundan;
T = m~2r
T = 0,1 · 22 · 0,5
v1 = 2v2 = 2v3 bulunur.
T = 0,2 N bulunur.
Yanıt B dir.
5.
y
ω
T
m
Nihat Bilgin Yayıncılık©
Yanıt E dir.
37°
m~2r
7.
mg
r
37°
Fs
r
y
Zeminin tepki kuvveti ile ağırlığın bileşkesi gerekli
merkezcil kuvveti oluşturur.
Taralı üçgenden;
tan37° =
mg
m~2 r
mg
C cisminin düşmemesi için cismin ağırlığı sürtünme
kuvvetine eşit olmalıdır.
~2 r
3
= g
4
2
C
~ · 1, 5
3
=
4
10
~ = 5 rad/s bulunur.
FS = mg
k · N = mg (Burada tepki kuvveti merkezcil kuvvete
2
Yanıt B dir.
v
km r = mg
eşit olmalıdır.)
Yanıt A dır.
17
ÇEMBERSEL HAREKET
8.
m
2m
10.
O
A
v
r
N
K
α
r
L
m
m ve 2m kütleli cisimlerin K ve L noktalarındaki
kinetik enerjileri, kaybettikleri potansiyel enerjilerine
eşittir.
2mgr =
1
2m v 2K
2
v 2K = 2gr
mg2r =
mg
1
m v 2L
2
v 2L = 4gr
vK
v2
tana = rg
NL
vL
NK =
2 m · v 2K
+ 2 mg
r
NL =
NK =
2 m · 2 gr
+ 2 mg
r
NL =
N K = 6 mg
m · v 2L
2r
+ mg
m · 4 gr
+ mg
2r
N L = 3 mg
Nihat Bilgin Yayıncılık©
mg
Aracın sürtünmesiz virajı geçebilmesi için ağırlıkla
tepki kuvvetinin bileşkesi gerekli merkezcil kuvveti
oluşturmalıdır. Taralı üçgenden;
v2
m r
tana = mg
NK
2mg
v2
r
bulunur.
Bu durumda eğim, aracın hızına ve virajın yarıçapına bağlıdır. Aracın kütlesine bağlı değildir.
Yanıt B dir.
11.
m
m
60°
NK
6 mg
=
= 2 bulunur.
NL
3 mg
r
r
O
O
Yanıt B dir.
Şekil I
Şekil I deki cisim saniyede 90° döndüğüne göre periyodu T1 = 4 s dir. Benzer şekilde Şekil II deki cismin periyodu da T2 = 6 s olur.
Merkezcil kuvvet;
F=m
4r2 r
T2
olduğu için, merkezcil kuvvetlerin oranı;
9. Çembersel hareket yapan bir cismin çizgisel hızı;
v = ~r = 2rfr olduğundan frekans büyütülürse çizgisel hız da açısal hız da büyür. Merkezcil ivme;
a = v~ olduğundan merkezcil ivme de büyür.
Yanıt C dir.
Şekil II
F1 = m
F2 = m
F1
F2
=
4r2 r
42
4r2 r
62
36
9
=
16
4
bulunur.
Yanıt A dır.
18
ÇEMBERSEL HAREKET
12.
14.Cismin düşmemesi için cisme
etki eden sürtünme kuvveti cismin
ağırlığına eşit olmalıdır.
37°
ip
r
T
F
İpteki gerilme kuvveti ile ağırlığın bileşkesi gerekli merkezcil kuvveti oluşturur. Merkezcil kuvvete F
dersek;
Fs
Fs = mg
m
k·N = mg
mg
Burada tepki kuvveti merkezcil
kuvvete eşittir.
k · m · 4r2R · f2 = mg
mg = 20N
ω
f=
R
g
Rk
1
2r
Yanıt A dır.
F
tan 37° = mg
3
F
=
4
20
F = 15 N
bulunur. Merkezcil ivme de F = m · a bağıntısından
7,5 m/s2 olarak bulunur.
Nihat Bilgin Yayıncılık©
Yanıt E dir.
15.
O
T
v
53°
mg·sin53°
13.
O
T
m
İpteki gerilme kuvveti merkezcil kuvveti oluşturur.
T = F = m·4r2r·f2 bağıntısında r, , ve f biliniyorsa
merkezcil ivme ve çizgisel hız bulunur. Fakat kütle
bilinmediğinden ipteki gerilme kuvveti bulunamaz.
Yanıt D dir.
m kütlesine merkez doğrultusunda etki eden kuvvetler şekilde gösterilmiştir. Bu kuvvetlerin bileşkesi merkezcil kuvveti oluşturur. Yani merkezcil kuvvet;
v2
m r = T – mg Sin53°
olur. Buradan çizgisel hız;
1
v2
= 33 – 1 · 10 · 0,8
1
v2 = 25
v = 5 m/s bulunur.
Yanıt D dir.
19
ÇEMBERSEL HAREKET
16.
m
A
Bu merkezcil kuvveti yayın uyguladığı kuvvet oluşturur. Yayın uzama miktarı;
Fyay = kx
ip
18 = 100 · x
x = 0,18 m = 18 cm
bulunur. Yayın serbest hâldeki uzunluğu;
50 – 18 = 32 cm bulunur.
vB
B
Yanıt D dir.
Cisim A noktasından geçerken ipteki gerilme kuvveti ile ağırlığın toplamı merkezcil kuvveti oluşturur.
m
m
v 2A
,
v 2A
,
= T + mg
= 3 mg + mg
v 2A = 4 g,
A noktasındaki mekanik enerji B noktasındaki mekanik enerjiye eşit olduğundan;
mg2, +
v 2A yerine 4g, yazılırsa;
mg2, +
Nihat Bilgin Yayıncılık©
1
1
mv 2A = mv 2B
2
2
1
1
m 4 g, =
m v 2B
2
2
v 2B = 8 g,
v 2B = 8 · 10 · 1
vB = 4 5 m/s bulunur.
Yanıt E dir.
18.
düşey
T
ω
37°
m
m~2r
mg
17.
37°
v
Fm
A
yatay
m
Cismin ağırlığı ile zeminin tepkisinin bileşkesi merkezcil kuvveti oluşturur. Taralı üçgenden;
Cismin merkezcil kuvveti;
tan37° =
v2
F=m r
F=1
32
0, 5
F = 18 N bulunur.
m~2 r
mg
5 2 ·r
3
=
10
4
r=
3
m = 30 cm bulunur.
10
Yanıt C dir.
20
ÇEMBERSEL HAREKET
19.
düşey
20.
~
v1
m
yatay
30°
T = 30N 30°
T
T
T
3T
v2
mg = 10N
Şekil I
m kütlesine etki eden kuvvetler Şekil I de gösterildiği gibidir. Bu kuvvetlerin bileşkesi merkezcil kuvveti oluşturur. Bu durumda merkezcil kuvvet 20 N
olur. Cisim sabit ~ açısal hızıyla döndürüldüğü
için en üst noktadan geçerken de merkezcil kuvvet
20 N olur.
v 21
m r = T + mg
v 22
m r = 3T – mg
T
~
yatay
Şekil II
En üst noktadan geçerken mg ile Tʹ gerilme kuvvetinin toplamı 20 N olmalıdır. Buna göre ipteki gerilme
kuvveti 10 N olur.
Yanıt A dır.
Nihat Bilgin Yayıncılık©
v 21
T = m r – mg
v 22
3 T = m r + mg
mg
düşey
En üst ve en alt noktada merkezcil kuvvet ifadesini
yazalım,
v 22 = 3 v 21 – 4 gr ................................ (1)
Enerjinin korunumundan;
1
1
mv 21 + mg 2 r = mv 22
2
2
v 22 = v 21 + 4 gr ....................(2)
(1) ve (2) denklemleri taraf tarafa toplanırsa;
2 v 22 = 4 v 21
v2 = 2 v1
v1
1
v2 = 2
bulunur .
Yanıt A dır.












