SÜPER POZİSYON TEOREMİ
Süper pozisyon yöntemi birden fazla kaynak içeren devrelerde uygulanır.
Herhangi bir elemana ilişkin akım değeri bulunmak istendiğinde, devredeki bir
kaynak korunup diğer tüm kaynaklar (iç empedansları hariç tutularak) devre
dışına çıkarılır (kaynakların devre dışına çıkarılması demek gerilim
kaynaklarının kısa devre, akım kaynaklarının ise açık devre yapılması anlamına
gelir). Bu şartlar altında istenen akım fazörü bulunur. Daha sonra ise devrede
tutulan kaynak devre dışına çıkarılarak (iç empedansı hariç ) bir önceki adımda
devre dışında tutulan kaynaklardan birisi devreye konulur ve istenilen elemana
ilişkin akım fazörü tekrar hesaplanır.Bu işlem tüm kaynaklar aynı işleme tabii
tutuluncaya kadar devam eder. Son adımda ise hesaplanan tüm akım fazörleri
toplanır ve elemanın gerçek akım fazörü elde edilir. Süper pozisyon teoremi
yalnız eleman akımlarının hesaplanmasında değil, eleman gerilimlerinin
hesaplanmasında da benzer şekilde uygulanır.
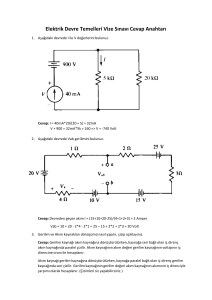
Örnek 1 ;
Şekilde verilen devrede kaynak empedansları ihmal edildiğine göre rezistans
üzerinden akan akım değerini süper pozisyon teoremini kullanarak bulunuz.
Çözüm :
Önce ikinci gerilim kaynağı kısa devre yapılmalıdır. Ortaya çıkan yeni devre
yukarıdaki şekilde gösterilmiştir. Kaynaktan bakıldığında görülen empedans
değeri ;
Z = XC1 + (R //XC2) =XC1 +R*XC2/R+XC2
XC1 = 1 / 2π (100) (0,02 * 0,001)= 79,58Ω
XC2 = 1 / 2π (100) (0,01 * 0,001)= 159,15Ω
Z = 79,58∠ -90° + 50∠0° * 159,15∠ -90° / 50∠0° + 159,15∠ -90°
Z = 104,32 ∠ -64,13° Ω
bulunur.
Kaynaktan çekilen akım ;
IK1 = VK1 / Z =80∠0° / 104,32∠ -64,13 =0,766∠ 64,13° A
elde edilir. Rezistans üzerinden geçen akım değeri akım bölücü ifadesi
kullanılarak ;
IR1 = (XC2 ∠ -90° / R – j XC2) * IK1
IR1 = (159,15∠-90° / 50-j 159,15) *(0,766∠ 64,13°)
IR1 = 0,73 ∠ 46,7° A
elde edilir.
İkinci adım olarak VK kısa devre edilerek devrede yalnızca VK2 bırakılır. Bu
durumda elde edilen devre aşağıdaki şekilde verilmiştir.
Kaynaktan bakıldığında görülen empedans değeri ;
Z = XC2 + R*XC1 / R+XC1
Z= 159,15∠ -90° + 50∠ 0°* 79,58 ∠ -90° / 50∠ 0° + 79,58∠ -90°
Z= 185,17∠ -78,84° Ω
bulunur.
Kaynaktan çekilen akım ;
IK2 =VK2 / Z =50∠0° / 185,17∠ -78,84 = 0,27∠ 78,84° A
elde edilir.Rezistans üzerinden gecen akım değeri akım bölücü ifadesi
kullanılarak ;
IR2 = (XC1∠ -90° /R - jXC1) IK2
IR2 = (79,58 ∠ -90° / 50 - j79,58)*(0,27∠78,84°) A
IR2 = 0,23 ∠ 46,7° A
elde edilir.
Rezistans üzerinden akan akım miktarı her iki adım sonucu bulunan akımların
toplamına eşit olacağından ;
IR = IR1 + IR2 = 0,73∠ 46,7° + 0,23 ∠46,7° A
IR = 0,958∠46,73° A
bulunur.
Örnek 2;
Yukarıda verilen devrede kaynak empedansları ihmal edildiğine göre bobin
üzerinden akan akımı süper pozisyon teoremini kullanarak bulunuz.
Çözüm ;
Önce IK2 kaynağı devre dışına çıkarılmalıdır. Akım kaynağının devre dışına
çıkarılması kaynağın açık devre yapılması anlamına gelir. IK2 akım kaynağı açık
devre yapıldığında bobin üzerinden geçen akım yalnızca IK1 akımı olacağından ;
IL1 = IK1 = 0,5∠ 0° A
olur.
İkinci adım olarak IK1 akım kaynağı devre dışına çıkarılmalıdır. Bu durumda L
ve C akım kaynağına seri olarak bağlı olacaktır. Akım kaynağına seri olarak
bağlanan yükler akım kaynağının değerinin değişmesinde etkili olamadıkları
için ;
IL2 = IK2 = 1∠ 90°
elde edilir.
Bobin üzerinden akan akım değeri ise ;
IL = IL1 + IL2 = 0,5∠ 0° +1∠ 90°
IL = 0,5 + j1= 1,118∠ 63,43° A
bulunur.
THEVENİN TEOREMİ
Alternatif akım devresini basitleştirerek onu eşdeğer bir alternatif gerilim
kaynağı ve bu kaynağa seri bağlı eşdeger empedansa dönüştürmek için thevenin
teoreminden faydalanılır.Thevenin teoreminin alternatif akım devrelerine
uygulanışındaki tek fark, doğru akım devrelerindeki kaynağın yerini alternatif
gerilim kaynağı, rezistansın yerini ise empedansın almasıdır.
Şekildeki devrede thevenin eşdeğer devresi gösterilmiştir. Verilen devre ne
kadar karışık olursa olsun thevenin teoremi kullanılarak devrede gösterilen
forma sokulabilir. Burada yapılması gereken işlem Vth ve Zth fazör değerlerinin,
basitleştirilmesi istenen devrenin elemanları yardımıyla bulunmasıdır. Zth değeri
omik, endüktif, kapasitif veya bunların kombinasyonlarından oluşabilir.
Thevenin eşdeğer gerilimi (Vth):
Vth gerilimi, yükün bağlandığı uçlar arasından bakıldığında ölçülen gerilim
fazörüne eşittir. Bu hesaplama yapılırken yük devre dışına çıkarılır, diğer bir
ifade ile yük uçları açık bırakılır ve hesaplamalara dahil edilmez. Aşağıda
verilen problem Vth değerinin hesabını göstermektedir.
Örnek 3 ;
Şekilde verilen devrede A – B uçları arasından görülen Vth değerini bulunuz.
Çözüm ;
Ryük devre dışına çıkarıldığında A-B uçları arasından bakıldığında bulunan
gerilim (Vth) ile XL uçları arasındaki gerilim değeri aynıdır. Gerilim bölücü
ifadesi kullanılarak XL uçları arasındaki gerilim değeri ;
VL = (XL ∠ 90° / R + jXL) Vk =(25∠90°/50+j25)*150∠0°
=(25∠90° / 55,9 ∠ 26,56°) *150∠0°
VL = VAB = Vth =67,084∠ 63,44° V
bulunur.
Thevenin eşdeğer empedansı (Zth):
Zth empedansı, yükün bağlandığı uçlar arasından bakıldığında ölçülen empedans
fazörüne eşittir. Bu hesaplama yapılırken devredeki kaynaklar (iç empedansları
hariç ) devre dışına çıkarılır, diğer bir ifade ile gerilim kaynakları kısa devre,
akım kaynakları ise açık devre yapılır. Zth bulunurken yük devre dışına çıkarılır,
diğer bir ifade ile yük uçları açık bırakılır ve empedans hesabına dahil edilmez.
Aşağıda verilen problem daha önce verilen ve Vth hesaplamaları yapılan
devrenin Zth değerlerinin hesabını göstermektedir.
Örnek 4 ;
Şekilde verilen devrede (Ryük devre dışına çıkarıldığında ) A-B uçları arasından
görülen Zth değerini bulunuz.
Çözüm ;
Ryük devreden uzaklaştırılıp gerilim kaynağı kısa devre yapıldığında ,AB uçları
arasından bakıldığında görülen thevenin empedans değeri aşağı hesaplanmıştır.
Zth = (R∠ 0° ) ( XL ∠ 90°) / R +jXL = ( 50 ∠0° ) ( 25∠90°) / 50+j25
= 1250 ∠ 90° / 55,901 ∠ 26,56° = 22,361 ∠ 63,44° Ω
Thevenin eşdeğer devresi ;
Daha önceden de bahsedildiği gibi karmaşık bir devrenin thevenin eşdeğeri, Vth
değerinde bir gerilim kaynağı ile buna Zth değerinde bir empedansın seri
bağlanması ile bulunur. Bundan önce verilen problemde devrenin Vth ve Zth
değerleri bulunmuştur. Aşağıda verilen problemde bulunan sonuçlar
toplanacaktır.
Örnek 5 ;
Şekilde verilen devrede AB uçları arasından bakıldığında görülen thevenin
eşdeğerini bulunuz.
Çözüm;
Şekilde verilen devrenin Vth gerilim değeri örnek 3’te Vth = 67,084∠63,44° volt
olarak bulunmuştu. Aynı devrenin Zth empedans değeri ise örnek 4’te
Zth = 22,361∠63,44°Ω = 10,11 + j20Ω olarak bulunmuştu.
Thevenin teoreminin özeti ;
Karmaşık devrenin yükü kaldırılıp yerine başka bir yük bağlandığında yeni
yükün çektiği akım ve uçları arasındaki gerilim değerini bulmak için karmaşık
işlemlerin tekrar yapılması gerekir. Karmaşık bir devrenin terine kullanılabilen
thevenin eşdeğer devresinin en önemli avantajı ise, yük kaldırılıp yerine yeni
yük bağlandığında thevenin eşdeğer devresi değişmeyeceğinden (yalnızca
thevenin devresinin çıkışına bağlanan yük değişeceğinden), thevenin devresinde
çözüm yapılması yeterli olmaktadır. Thevenin devresi gerilim kaynağı ve ona
seri bağlı bir empedansı içerdiğinden, bunun çıkışına yeni bir yük
bağlandığında, yük akım ve gerilimini bulmak için yapılacak işlem kısa sürede
tamamlanabilir. Thevenin teoremi dört adımda özetlenebilir;
Thevenin eşdeğerini bulmak için devreye hangi iki uç arasından bakılıyor ise
bu uçlar açık devre yapılır ve bu uçlara bağlı empedans devreden
uzaklaştırılır.
Bu iki uç arasındaki Vth gerilim değeri hesaplanır.
Devredeki tüm kaynaklar devre dışına çıkarılarak (iç empedansları hariç) iki
uç arasındaki Zth empedans değeri hesaplanır. Kaynakların devre dışına
çıkarılması, akım kaynaklarının kısa devre, gerilim kaynaklarının açık devre
yapılması anlamına gelir.
İkinci ve üçüncü adımlardan bulunan Vth ve Zth değerleri seri olarak
bağlanarak thevenin eşdeğer devresi oluşturulur. Thevenin eşdeğer devresi
başlangıçta açık devre yapılan iki uç arasına bağlanır.
NORTON TEOREMİ ;
Norton teoremi de thevenin teoremi gibi karmaşık devrelerin birleştirilmesi için
geliştirilmiştir. Norton teoreminde kullanılan eşdeğer devre, IN akım kaynağı ve
ona paralel ZN empedansından meydana gelir. Norton teoremi bu iki eleman
değerinin hesaplanmasını açıklar. Aşağıdaki şekilde norton eşdeğer devresi
gösterilmiştir.
Norton eşdeğer akım kaynağı (IN) ;
IN, verilen devrede iki nokta (A-B) arasındaki kısa devre akım değeri olarak
tanımlanabilir. Aşağıdaki şekil (a)’da verilen (kutu içinde) karmaşık devrenin
çıkışına (A-B) arasına bağlanan yük (şekilde Ryük) kaldırılır ve çıkış kısa devre
yapılırsa, A-B arasından akan akım fazör değeri (şekil (b)) IN bulunur.
Örnek 6 ;
Aşağıdaki şekilde verilen devrede A-B uçları kısa devre yapıldığında ölçülen IN
değerini bulunuz.
Çözüm ;
Yukarıdaki verilen devrede A-B uçları kısa devre yapılırsa aşağıda görülen
devre bulunur. Aşağıdaki şekilde kaynaktan bakıldığında görülen eşdeğer
empedans ;
Z=XC1+R*XC2 / R+XC2 = 15∠-90°+(5∠0°)(15∠-90°) / 5-j15 = 17,1∠74,7°Ω
bulunur. Kaynaktan çekilen akım değeri ise ;
IK = VK / Z = 10∠0° / 17,1∠74,7° =0,584∠-74,7° A
elde edilir. A-B uçları arasından akan akım ise akım bölücü ifadesi kullanılarak ;
IN=(R/R+XC2)Ik=(5∠0°/5-j15)(0,584∠-74,7°)=0,184∠-3,14°Ω
bulunur.
Norton eşdeğer empedansı (ZN) ;
Norton eşdeğer devresinde kullanılan ZN empedansı, verilen devrede kaynaklar
devre dışında bırakıldığında A-B uçları arasından bakıldığında görülen eşdeğer
empedans değerine eşittir. Bu tanıma bakıldığında ZN = Zth olduğu anlaşılır.
Örnek 7 ;
Örnek 6’daki şekilde verilen devrede A-B uçları arasından bakıldığından ölçülen
ZN değerini bulunuz.
Çözüm ;
Örnek 6’da verilen devrede A-B uçları arası açık devre ve gerilim kaynağı kısa
devre yapılırsa aşağıda verilen devre bulunur. Aşağıdaki şekilde kaynaktan
bakıldığında görülen eşdeğer empedans ;
ZN=XC2+R*XC1/R+XC1=15∠-90°+(5∠0°)(15∠-90°)/5-j15=17,1∠-74,7°Ω
ZN=4,51-j16,5Ω
bulunur.
Norton teoreminin özeti;
Norton teoreminin faydası thevenin teoremi ile aynıdır.Bazı devrelerde thevenin
eşdeğer devresinin kullanılması uygun olurken bazı devrelerde basitleştirme
sağlamak için norton teoreminin kullanılması hesaplamaları kolaylaştırır. Norton
teoremini dört adımda özetleyebiliriz.
Norton eşdeğerini bulmak için devreye hangi iki uç arasından bakılıyorsa bu
uçlar kısa devre yapılır.
Devrede tüm kaynaklar mevcutken kısa devre yapılan iki uç arasından akan
IN akım değeri hesaplanır.
Devredeki tüm kaynaklar devre dışına çıkarılarak , iki uç ise açık devre
yapılarak iki uç arasından görülen ZN empedans değeri hesaplanır.
Kaynakların devre dışına çıkarılması , akım kaynaklarının kısa devre ,gerilim
kaynaklarının açık devre yapılması anlamına gelir.
İkinci ve üçüncü adımlardan bulunan IN akım kaynağına ZN değeri paralel
olarak bağlanır ve norton eşdeğer devresi bulunur. Norton eşdeğer devresi
başlangıçta açık devre yapılan iki uç arasına bağlanır.
MAXİMUM GÜÇ (TRANSFER) TEOREMİ
Bir devre çıkışına bağlanan yükün o devreden maximum güç çekebilmesi için,
yük empedansı devre çıkış empedansının kompleks eşlenik değerine eşit
olmalıdır. Bu ifade maximum güç transfer teoremi olarak adlandırılır.
Maximum güç transfer teoremi başka bir şekilde de ifade edilebilir ; Bir devre
çıkışına bağlanan yükün o devreden maximum güç çekebilmesi için ,devrenin
yükün bağlandığı uçlar arasından bakıldığında görülen thevenin empedansının
kompleks eşleneği , yük empedansına eşit olmalıdır. Eğer devre çıkışına
bağlanan yük değeri Zyük = a + jb ise bunun kompleks eşleniği Zyük = a – jb
olur.
Örnek 8;
Karmaşık bir devrenin A-B uçları arasından bakıldığında görülen thevenin
eşdeğer empedansının 20Ω değerinde omik bir yük ile buna seri bağlı
L= 0,159 H değerinde bir bobinden oluştuğu görülmüştür. Karmaşık devrenin
A-B uçları arasında bakıldığında görülen thevenin kaynak gerilim değeri ise
f= 50 Hz için Vth =30∠0° V (etkin) olarak hesaplanmaktadır. Verilen karmaşık
devrenin çıkışına R=20Ω değerinde omik bir yük ve buna seri bağlı C= 63,66µF
değerinde bir kapasitör bağlanmaktadır. f= 20Hz , 50Hz ve 100Hz için yükün
çektiği aktif güç değerlerini bulunuz.
Çözüm;
Aşağıdaki şekilde verilen devre gösterilmiştir.
f= 20Hz için
XC= 1/ 2π * 20 * 63,66 * 0,000001 = 125Ω
XL = 2π * 20 *0,159 = 19,98Ω
bulunur.
Devrenin toplam empedans genliği;
Zt= Z = √(20+20)*(20+20) + (19,98-125)(19,98-125) =112,38Ω
elde edilir. Kaynaktan çekilen akım (etkin ) değeri ;
I = Vk / Z = 30 / 112,38 = 0,267 A
bulunur. Yük üzerinde harcanan aktif güç değeri ;
Pyük =I*I Ryük = (0,267)(0,267)*20 = 1,425 W
elde edilir.
f=50Hz için;
XC = 1/2π*50*63,66*0,000001 = 50Ω
XL = 2π*50*0,159 = 50Ω
bulunur. Devrenin toplam empedans genliği;
Zt=Z=√(20+20)(20+20)+(50-50)(50-50)=20Ω
elde edilir. Kaynaktan çekilen akım değeri;
I = Vk / Z = 30 / 20 = 1,5 A
bulunur. Yük üzerinde harcanan aktif güç değeri;
Pyük = I*I*Ryük =(1,5)(1,5)*20 = 45 W
elde edilir.
f=100Hz için
XC = 1 / 2π*100*63,66*0,000001 = 25Ω
XL = 2π*100*0,159 = 100Ω
bulunur.
Devrenin toplam empedans genliği;
Zt=Z=√(20+20)(20+20)+(100-25)(100-25) = 85Ω
elde edilir. Kaynaktan çekilen akım değeri;
I = Vk / Z = 30 / 85 = 0,352 A
bulunur. Yük üzerinde harcanan aktif güç değeri;
Pyük = I*I*Ryük = (0,352)(0,352)*20 = 2,478 W
elde edilir.
Bulunan güç değerlerinden de görüldüğü gibi f=50Hz için kaynak empedansı ile
yük empedansı birbirlerini kompleks eşleniği oldukları için yükte harcanan aktif
güç değeri maximum olmaktadır. Empedans değeri frekans değeri ile değiştiği
için verilen problem için güç ile frekans değişimi şekilde gösterilmiştir. Şekilde
de görüldüğü gibi 50Hz için yükte tüketilen güç maximum olmaktadır.
Örnek 9 ;
Yukarıdaki şekilde kuvvetlendirici ve bunun gerisindeki Vgiriş gerilimi,
hoparlörü besleyen kaynak olarak kabul edildiğinde, ayar kapasitörünü de içeren
sistem eşdeğeri şekilde gösterilmiştir. Hoparlörden maximum güç çekilebilmesi
için kaynak frekansı ne olmalıdır? Kaynak gerilim etkin değeri 3,8 V olduğunda
hoparlör tarafından çekilen güç değerini bulunuz.
Çözüm ;
Maximum güç teoreminde anlatıldığı gibi hoparlörün kaynaktan maximum güç
çekebilmesi için kaynak empedansı ile yükün empedansının birbirlerinin
eşleniği olması gerekir. Buna göre;
XL = XC ⇒ 1 / 2πfC = 2πfL
olmalıdır. Bu eşitliği sağlayan frekans ise;
f*f = 1 / 4π*4πLC ⇒ f= 1 / 2π√ LC = 1 / 2π√ 0,1*0,1*0,000001 = 1592Hz
bulunur. Devrenin toplam empedansı ise;
Zt = Rçıkış + Rhop = 16Ω
elde edilir. Kaynaktan çekilen akım değeri;
I = Vk / Zt = 3,8 / 16 = 0,238 A
olur.
Hoparlörde harcanabilecek maximum güç ise;
Pmax = I*I*Rhop = (0,238)(0,238)*8 = 0,453 W
bulunur.