• Ödev1: 600N’luk kuvveti
u ve v eksenlerinde
bileşenlerine ayırınız.
600 N
600 N
Fu
600 N
=
sin 120° sin 30°
Fv
600 N
=
sin 30° sin 30°
600 N
Fu = 1039 N
Fv = 600 N
600 N
• Ödev2: F2 kuvvetinin
şiddetini, yönünü ve bileşke
kuvveti bulunuz. (bileşke
kuvvet x ekseni üzerinde, F2
kuvveti ise minimum şiddette
olsun)
• Ödev2: F2 kuvvetinin
şiddetini, yönünü ve bileşke
kuvveti bulunuz. (bileşke
kuvvet x ekseni üzerinde, F2
kuvveti ise minimum şiddette
olsun)
• Ödev3: Etkiyen
kuvvetlerin
bileşkesinin y ekseni
boyunca olması ve
şiddetinin de 800 N
olması için F1
kuvvetinin şiddetini,
θ açısının ne olması
gerektiğini bulunuz
r
r r r
FR = F1 + F2 + F3
FRy = 800 N
FRx = 0
4
∑ FRx = − 600 × 5 + F1 × sin θ + 400 × cos 30 = 0
− 480 + F1 × sin θ + 346.41 = 0
F1 × sin θ = 133.59 N
133.59
F1 =
sin θ
3
∑ FRy = 600 × 5 + F1 × cosθ + 400 × sin 30 = 800
240
F1 × cos θ = 240 N
F1 =
cos θ
133.59 240
=
sin θ
cos θ
133.59
= tan θ
240
θ = 29.1
133.59
F1 =
= 275 N
sin 29.1
• ÖDEV4: Şekilde
gösterilen kuvvetlerin
bileşkesini birim
vektörleri kullanarak
bulunuz
• ÖDEV4: Şekilde
gösterilen kuvvetlerin
bileşkesini birim
vektörleri kullanarak
bulunuz
ÇÖZÜM 1:
ÇÖZÜM 2:
• ÖDEV5: F kuvvetini
kartezyen vektör
olarak ifade ediniz
ve F kuvvetinin yön
kosinüslerini
bulunuz
r r r
F = F '+ Fz
r r r
F ' = Fx + Fy
• ÖDEV 6: A noktasına
etki eden kuvveti
kartezyen vektör
olarak ifade edin.
Ödev 7
W
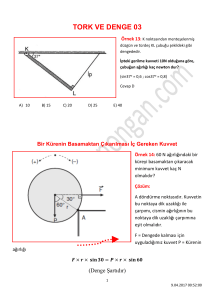
• Şekilde gösterilen
kablolarda 0.5 kN’un
üzerinde çekme
kuvveti oluşmaması
için asılı olan kovanın
ağırlığını (W)
bulunuz.
E noktasının SCD’ı
3
⎯
⎯→ ∑ Fx = 0 FED . cos 30 − FEB ( ) = 0
5
FED = 0.693FEB
+
4
↑ ∑ Fy = 0 FED . sin 30 + FEB ( ) − W = 0
5
0.8 FEB + 0.5(0.693FEB ) = W
FEB = 0.872W
⎣1⎦
B noktasının SCD’ı
3
⎯
⎯→ ∑ Fx = 0 FBC . cos 30 + FBE ( ) − FBA = 0
5
4
↑ ∑ Fy = 0 FBC . sin 30 + FBE ( ) = 0
5
0.5 FBC = 0.8 FBE = 0.8 × 0.872W
+
⎣2⎦
FBC = 1.395W
1.395W (cos 30) + 0.6(0.872W ) = FBA
FBA = FAB = 1.731W
⎣3⎦
En riskli durum [3]
0.5 = 1.731W
W = 0.289kN
Ödev 8
6
m
3
m
• Sokak lambasını
kaldırmak için F
kuvvetinin A
noktasında 2250 Nm
saatin tersi yönünde
moment oluşturması
gerekmektedir. Bu
durumda F kuvvetinin
şiddeti ne olmalıdır?