ÖRNEK SORULAR

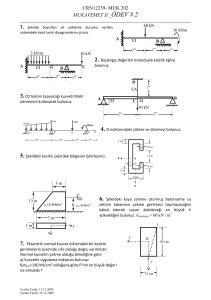
ÖRNEK SORULAR
1. f : \ → \, f ( x) = x 2 − 4 x + 3 fonksiyonu veriliyor. Aşağıdaki kümeleri bulunuz:
a) f ([2,3])
b) f ((−3, 0))
c) f −1 ({−18})
d) f −1 ((4, 7))
x+2
⎧ 1⎫
⎧1 ⎫
fonksiyonu veriliyor.
2. f : \ \ ⎨ − ⎬ → \ \ ⎨ ⎬ , f ( x) =
3x + 1
⎩ 3⎭
⎩3⎭
a) f fonksiyonunun bire-bir ve örten olduğunu gösteriniz.
b) f −1 fonksiyonu var mıdır? Varsa, bulunuz.
c) f −1 ({−1, 0}) kümesini bulunuz.
⎧ x 2 − 3 x, x ≥ 2 ise
3. f ( x) = ⎨
x < 2 ise
⎩ x + 2,
a) f (0) nedir?
b) f ([1,3]) kümesini bulunuz.
olarak tanımlanan f : \ → \ fonksiyonu veriliyor.
4. İki elemanlı bir kümeden üç elemanlı bir kümeye tanımlanabilecek bütün fonksiyonları
bulunuz.
5. n elemanlı bir kümeden m elemanlı bir kümeye tanımlanabilecek bütün farklı fonksiyonların
sayısı nedir? Bire-bir olanların sayısı nedir?
6. f : X → Y olsun. Aşağıdakileri kanıtlayınız.
a) A, B ⊆ X için A ⊆ B ise f ( A) ⊆ f ( B) dir.
b) C ⊆ Y için f −1 (Y \ C ) = X \ f −1 (C ) dir.
7. f : X → Y ve A ⊆ X olsun. f | A = g dersek, B ⊆ Y için
g −1 ( B ) = A ∩ f −1 ( B)
eşitliğini gösteriniz.
8. f : X → Y ve B1 , B2 ⊆ Y olsun.
f −1 ( B1 \ B2 ) = f −1 ( B1 ) \ f −1 ( B2 )
eşitliğini kanıtlayınız.
9. ∀m, n, p, q ∈ ` için n < m ve p < q ⇒ np < mq olduğunu gösteriniz.
10. Doğal sayılarda toplamanın değişme özelliğini, toplama tanımını kullanarak ispatlayınız.
11. Aşağıdaki ifadeleri tümevarımla gösteriniz.
1
1
1
n
a)
+
+ ... +
=
1.2 2.3
n.(n + 1) n + 1
1 2 3
n
n+2
b) + 2 + 3 ... + n = 2 − n
2 2 2
2
2