DERS:
ÜNİTE:
KONU:
MATEMATİK I
FONKSİYONLAR
MAT101(04)
4. TRİGONOMETRİK FONKSİYONLAR
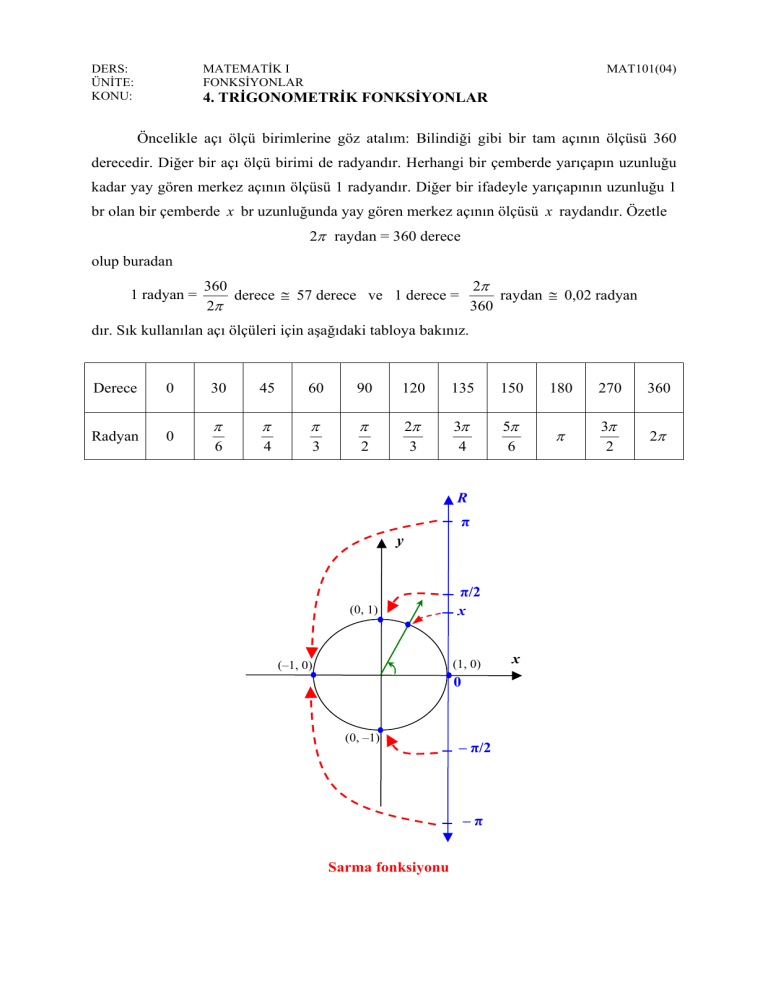
Öncelikle açı ölçü birimlerine göz atalım: Bilindiği gibi bir tam açının ölçüsü 360
derecedir. Diğer bir açı ölçü birimi de radyandır. Herhangi bir çemberde yarıçapın uzunluğu
kadar yay gören merkez açının ölçüsü 1 radyandır. Diğer bir ifadeyle yarıçapının uzunluğu 1
br olan bir çemberde x br uzunluğunda yay gören merkez açının ölçüsü x raydandır. Özetle
2π raydan = 360 derece
olup buradan
1 radyan =
360
2π
derece ≅ 57 derece ve 1 derece =
raydan ≅ 0,02 radyan
2π
360
dır. Sık kullanılan açı ölçüleri için aşağıdaki tabloya bakınız.
Derece
0
30
45
60
90
120
135
150
180
270
360
Radyan
0
π
6
π
4
π
3
π
2
2π
3
3π
4
5π
6
π
3π
2
2π
R
π
y
π/2
x
(0, 1)
x radyan
(–1, 0)
(1, 0)
0
(0, –1)
– π/2
–π
Sarma fonksiyonu
x
y
R
tanx
(0, 1)
R
cotx
P(cosx,sinx)
sinx
(–1, 0)
O
x
cosx
x
(1, 0)
(0, –1)
Trigonometrik fonksiyonlar
Şekildeki birim çemberde [OP ışını çemberi P noktasında keser ve bu ışın ile
Ox − ekseninin pozitif yönde oluşturduğu açının ölçüsü
x
raydan olsun. Sarma
fonksiyonunun tanımından açıkça, x reel sayısı sarma fonksiyonu ile P noktası ile eşlenir.
Bu durumda x reel sayısının kosinüsü ( cos x ), P noktasının apsisi olarak tanımlanır. Benzer
şekilde
x reel sayısının sinüsü ( sin x ), P noktasının ordinatı olarak tanımlanır. Öyleyse
kosinüs ve sinüs; tanım kümeleri R ve değer kümeleri [−1, 1] aralığı olan fonksiyonlardır.
Özetle cos : R → [−1, 1] ve sin : R → [−1, 1] fonksiyonları sınırlıdır.
Ayrıca sin ve cos fonksiyonlarından faydalanarak
tan : R − {(2k + 1) π2 : k ∈ Z } → R ,
tan x =
sin x
cos x
cot : R − {kπ : k ∈ Z } → R ,
cot x =
cos x
sin x
sec : R − {(2k + 1) π2 : k ∈ Z } → R − (−1, 1) ,
sec x =
1
cos x
cosec : R − {kπ : k ∈ Z } → R − (−1, 1) ,
cot x =
1
sin x
fonksiyonları tanımlanır.
2
Yukarıda tanımlanan trigonometrik fonksiyonları içeren temel bağıntıların bir kısmı aşağıda
verilmiştir.
cos 2 x + sin 2 x = 1
tan x cot x = 1
cos(− x) = cos x , sin(− x) = − sin x , tan(− x) = − tan x , cot(− x) = − cot x
cos( x + y ) = cos x cos y − sin x sin y
sin( x + y ) = sin x cos y + sin y cos x
tan( x + y ) =
tan x + tan y
1 − tan x tan y
cos(x − π2 ) = sin x , sin (x + π2 ) = cos x
cos( π2 − x ) = sin x , sin ( π2 − x ) = cos x
tan (π2 − x ) = cot x , cot (π2 − x ) = tan x
cos 2 x = cos 2 x − sin 2 x = 2 cos 2 x − 1 = 1 − 2 sin 2 x
sin 2 x = 2 sin x cos y
tan 2 x =
2 tan x
1 − tan 2 x
sin x sin y =
1
2
[cos( x − y ) − cos( x + y )]
sin x cos y =
1
2
[sin( x + y ) + sin( x − y )]
cos x cos y =
1
2
[cos( x + y ) + cos( x − y )]
x+ y
x− y
sin x + sin y = 2 sin
cos
2
2
x+ y
x− y
cos x + cos y = 2 cos
cos
2
2
3
x
0
π
6
π
4
π
3
π
2
cos x
1
3
2
2
2
1
2
0
sin x
0
1
2
2
2
3
2
1
2π
3
3π
4
5π
6
π
7π
6
tan x
cot x
sec x
cosecx
* Temel trigonometrik bağıntılardan yararlanarak tablonun kalan kısmını doldurunuz.
5π
4
4π
3
3π
2
5π
3
7π
4
11π
6
2π
Tanım: f : A → R , y = f (x) fonksiyonu verilsin. Her x ∈ A için f ( x + T ) = f ( x) olacak
şekilde bir pozitif T ∈ R + sayısı varsa f fonksiyonu periyodiktir, T ye de f fonksiyonunun
bir periyodudur denir. Bu şekildeki tanımlı T sayılarının en küçüğüne (eğer varsa) f
fonksiyonunun (esas) periyodu denir.
Örnek: f : R → [−1, 1] , f ( x) = sin x fonksiyonu periyodik midir?
Ödev: Yukarıda tanımladığımız trigonometrik fonksiyonların periyodik olduğunu göstererek
esas periyodlarını bulunuz.
Teorem: m ∈ Z + , a, b ∈ R ve a ≠ 0 olsun. Bu durumda
1) sin m (ax + b) ve cos m (ax + b) fonksiyonlarının esas periyodu
π
2π
m tek ise T =
, m çift ise T =
|a|
|a|
2) tan m (ax + b) ve cot m (ax + b) fonksiyonlarının esas periyodu T =
Örnek: Aşağıda verilen fonksiyonların periyodlarını bulunuz.
a) f : R → R , f ( x) = sin x + cos 2 x
b) g : R − {(2k + 1) 12 : k ∈ Z } → R , g ( x) = 5 + tan (πx )
x
x
c) h : R → R , h( x) = sin 3 + cos 4
4
3
Trigonometrik Fonksiyonların Grafikleri
π
|a|
y = cosx
y = sinx
y = tanx
y = cotx
y = secx
y = cosecx
6
Ters Trigonometrik Fonksiyonlar
f : R → [−1, 1] , f ( x) = sin x fonksiyonu örtendir ancak 1-1 değildir. Bu fonksiyonun tanım
π π
kümesi − , aralığına kısıtlandığında elde edilen yeni fonksiyon 1-1 ve örten olup tersi
2 2
vardır. Bu fonksiyonun tersi;
π π
Arc sin : [−1, 1] → − , , y = Arcsinx
2 2
π π
fonksiyonudur. Açık olarak y ∈ − , için
2 2
y = Arcsinx ⇔ x = Siny
y = Sinx
Örnek: Arc sin
2
2
y = Arcsinx
ve Arc sin (− 12 ) ifadelerini hesaplayınız.
Benzer şekilde f : R → [−1, 1] , f ( x) = cos x fonksiyonu örtendir ancak 1-1 değildir. Bu
fonksiyonun tanım kümesi [0, π ] aralığına kısıtlandığında elde edilen yeni fonksiyon 1-1 ve
örten olup tersi vardır. Bu fonksiyonun tersi;
Arccos : [−1, 1] → [0, π ] , y = Arccosx
fonksiyonudur. Açık olarak y ∈ [0, π ] için
y = Arccosx ⇔ x = Cosy
y = Cosx
y = Arccosx
7
Benzer şekilde f : R − {(2k + 1) π2 : k ∈ Z } → R , f ( x) = tan x fonksiyonu 1-1 ve örten değildir.
π π
Bu fonksiyonun tanım kümesi − , aralığına kısıtlandığında elde edilen yeni fonksiyon
2 2
1-1 ve örten olup tersi vardır. Bu fonksiyonun tersi;
π π
Arctan : R → − , , y = Arctanx
2 2
π π
fonksiyonudur. Açık olarak y ∈ − , için
2 2
y = Arctanx ⇔ x = Tany
y = Tanx
y = Arctanx
Aynı düşünceyle Cot : (0, π ) → R , y = Cotx fonksiyonu 1-1 ve örten olup tersi
Arccot : R → (0, π ) , y = Arccotx
fonksiyonudur. y ∈ (0, π ) için
y = Arccotx ⇔ x = Coty
olur.
y = Cotx
y = Arccotx
8
ÖRNEKLER
1.
1
1
= ? , arccos = ?
2
2
1
1
b) Arcsin = ? , arcsin = ?
2
2
c) Arctan 3 = ? , arctan 3 = ?
a) Arccos
2. Aşağıdaki denklemleri çözünüz.
a) tan x = 1
b) sin x = 1
c) cosx = −
1
2
d) co sec x = 2
3. Aşağıda verilen fonksiyonların en geniş tanım kümelerini bulunuz.
x
2x + 1
a) y = arcsin
b) y = arctan
5
x−2
4. Aşağıdaki bağıntıların doğruluğunu gösteriniz.
a) cos(arcsin x) = 1 − x 2
b) sin(arccos x) = 1 − x 2
c) arcsin(cos x) = π2 − x
x
d) tan(arcsin x) =
1− x2
x+ y
e) arctan x + arctan y = arctan
1− x y
ÖDEVLER
M. BALCI, Genel Matematik Cilt I
Sayfa 66-68 Problemler
C.H. EDWARDS, D.E. PENNY, Matematik Analiz ve Geometri Cilt I
Sayfa 33-36 Trigonometrik Fonksiyonlar konusunu okuyunuz.
Sayfa 42-44 Problemler 11-30
Sayfa 44-45 1.4. Proje: Bir Küresel Astroid
KAYNAKLAR
M. BALCI, Genel Matematik Cilt I, Balcı Yayınları, Ankara, 2003.
C.H. EDWARDS, D.E. PENNY, Matematik Analiz ve Geometri Cilt I, (çev.ed. Ömer AKIN), Palme Y., Ankara, 2001.
9










