İç-Çarpım Uzayları
ÜNİTE
10
Yazar
Öğr. Grv. Dr. Nevin ORHUN
Amaçlar
Bu üniteyi çalıştıktan sonra;
• Rn, Pn (R), Mnxn vektör uzaylarında iç çarpım kavramını tanıyacak ve özelliklerini görmüş olacaksınız.
• Rn, Pn (R), Mnxn uzaylarında bir vektörün uzunluğu ve iki vektör arasındaki açı kavramlarını öğreneceksiniz.
• İki vektörün ortogonal olmasını,
• Bir kümenin ortogonal ve ortonormal olmasını,
• Sonlu boyutlu bir vektör uzayının Gram-Schmidt yöntemi ile
daima bir ortonormal tabanının bulunabileceğini öğreneceksiniz.
İçindekiler
• Giriş
217
• Vektörlerin Ortogonalliği, Ortonormal Vektör Kümeleri
227
• Değerlendirme Soruları
233
Çalışma Önerileri
• Vektör uzayları ünitesini yeniden gözden geçiriniz.
ANADOLU ÜNİVERSİTESİ
İÇ-ÇARPIM UZAYLARI
1. Giriş
R2 ve R3 vektör uzaylarında bir vektörün uzunluğu, iki vektör arasındaki açı
kavramlarını ve bu kavramların bu uzaylara kazandırdığı kimi önemli özellikleri
Analitik Geometri derslerinden biliyorsunuz. Eğer sadece R2 ve R3 uzayındaki
vektörleri incelemiş olsaydık orada verilen uzunluk ve açı tanımları yeterli olurdu.
Fakat daha önce gördüğümüz Pn(R) vektör uzayındaki iki polinom arasındaki
açıdan veya Mmxn vektör uzayındaki bir matrisin uzunluğundan söz edilebilir
mi? Daha genel olarak, herhangi bir vektör uzayına bu kavramlar genelleştirilebilir mi? Bu tür sorulara yanıt verebilmek için bir vektör uzayı içinde iç çarpım kavramını tanımlıyacağız.
1.1. İç Çarpım Uzayları
V bir vektör uzayı olsun. x, y ∈V için < x, y > ile gösterilen ve aşağıdaki koşulları sağlayan < , > : V x V → R , (x, y) → < x, y > fonksiyonuna V üzerinde bir
iç çarpım V ye de iç çarpım uzayı denir. Bu iç çarpım uzayı (V, < , >) ile gösterilir.
(i) Her x, y ∈V
için < x, y > = < y, x >
(ii) Her x, y, z ∈V için < x, y + z> = < x, y > + < x, z >
(iii) Her x, y ∈V , c∈ R için
< cx, y > = c< x, y > = < x, cy >
iv) Her x ∈V için < x, x > ≥ 0 ; < x, x > = 0 ⇔ x = 0
1.2. Örnek
Rn de iç çarpım:
x, y ∈ R için x = (x1 , x2 , ..., xn) , y = (y1 , y2 , ..., yn)
olsun.
x ve y vektörlerinin iç çarpımı
< x, y > = x1 y1 + x2 y2 + ... + xn yn
biçiminde tanımlanır.
Bu tanımın iç çarpımın tüm koşullarını sağladığı kolayca doğrulanabilir. Aşağıdaki teorem ile n = 3 için kanıt verilmektedir. Rn ne bu iç çarpımla öklid uzayı adı
verilir.
1.3. Teorem
R3 içindeki x = ( x1 , x2 , x3 ) , y = ( y1 , y2 , y3 ) vektörleri için
< x, y > = x1 y1 + x2 y2 + x3 y3
bir iç çarpımdır.
AÇIKÖĞRETİM FAKÜLTESİ
217
218
İÇ-ÇARPIM UZAYLARI
Kanıt
< x, y > nin bir iç çarpım olduğunu göstermek için iç çarpım tanımındaki i-iv koşullarının sağlandığını göstermeliyiz.
(i) < x, y > = x1 y1 + x2 y2 + x3 y3
= y 1 x1 + y2 x2 + y3 x3
= < y, x >
(ii) < x, y + z > =
=
=
=
=
iii) < cx, y > =
=
=
=
< ( x1 , x2 , x3 ) , ( y1 + z1 , y2 + z2 , y3 + z3 ) >
x1 ( y1 + z1 ) + x2 ( y2 + z2 ) + x3 ( y3 + z3 )
x1 y1 + x1 z1 + x2 y2 + x2 z2 + x3 y3 + x3 z3
x1 y1 + x2 y2 + x3 y3 + x1 z1 + x2 z2 + x3 z3
< x, y > + < x, z >
< ( cx1 , cx2 , cx3 ) , ( y1 , y2 , y3 ) >
cx1 y1 + cx2 y2 + cx3 y3
c( x1 y1 + x2 y2 + x3 y3 )
c < x, y >
iv) < x, x > = < ( x1 , x2 , x3 ) , ( x1 , x2 , x3 ) >
= x12 + x22 x32 ≥ 0
Böyle bir toplamın sıfır olması her terimin ayrı ayrı sıfır olmasıyla sağlanacağından
x 1 = x2 = x3 = 0
dır. < x, x > = 0 ⇔ x = 0
Böylece R3 de
< x, y > = x1 y1 + x2 y2 + x3 y3
bir iç çarpım olduğu kanıtlanmış olur.
1.4. Örnek
R3 teki x = (2, -3, 1), y = (1, 5, -6) vektörlerinin iç çarpımını hesaplayınız.
Çözüm
< x, y > =
=
=
=
x 1 y 1 + x2 y 2 + x3 y 3
2.1 + (-3).5 + (1.(-6)
2 - 15 - 6
-19
ANADOLU ÜNİVERSİTESİ
İÇ-ÇARPIM UZAYLARI
219
1.5. Örnek
Pn(R) de iç çarpım:
Pn(R), derecesi n veya n den küçük olan polinomların uzayında iç çarpım;
p(x), q(x) ∈ Pn(R) için
1
< p(x), q(x) > =
0
p(x) . q(x) dx
biçiminde tanımlanır. Bu tanımın iç çarpım koşullarını sağladığını kolayca doğrulayabilirsiniz.
1.6. Örnek
P2 (R) de p(x) = 3x2 + 2x + 5 , q(x) = x + 1 vektörlerinin iç çarpımlarını hesaplayınız.
Çözüm
< p(x), q(x) > = < 3x2 + 2x + 5 , x + 1 > =
=
1
0
1
0
(3x2 + 2x + 5) . (x + 1) dx
(3x3 + 5x2 + 7x + 5) dx
= 3 x4 + 5 x3 + 7 x2 + 5x
4
3
2
1
0
= 3 +5 +7 + 5
4 3
2
= 131
12
1.7. Örnek
Mnxn uzayında iç çarpım:
A, B ∈ Mnxn , A = (aij)nxn , B = (bij)nxn olmak üzere
< A, B > =
n
n
∑ ∑
a ij bij
i=1 j=1
biçiminde tanımlanır. Bu tanımın iç çarpım koşullarını sağladığının gösterilmesini alıştırma olarak bırakıyoruz.
AÇIKÖĞRETİM FAKÜLTESİ
220
İÇ-ÇARPIM UZAYLARI
1.8. Örnek
1 2
M2x2 de A =
,B =
3 4
vektörlerinin iç çarpımlarını hesaplayınız.
1 -3
2
2
∑ ∑
< A, B > =
2 0
a ij bij
i=1 j=1
2
∑
=
a i1 bi1 + a i2 bi2
i=1
= a 11 b11 + a 12 b12 + a 11 b11 + a 12 b22
buna göre,
= 1.2 + 2.0 + 3.1 + 4(-3)
= -7
bulunur.
1.9. Tanım
A = (aij)nxn matrisi verilsin.
A =
a 11
a 12
a 1n
a 21
a 22
a 2n
a n1
a n2
a nn
A matrisinin köşegeni üzerindeki sayıların toplamı olan
a11 + a22 + ... + ann
sayısına A matrisinin izi denir
iz (A) = a 11 + a 22 + ... + a nn =
n
∑
a ii
i=1
biçiminde gösterilir.
Mnxn vektör uzayındaki A, B ∈ Mnxn için iç çarpım
< A, B > = iz ( AB t ) =
n
n
i
j
∑ ∑ a ij bij
dir. Çünkü ABt çarpımında köşegen üzerindeki elemanların toplamı
iz (A B t) =
n
n
i
j=1
∑ ∑
a ij btij
dir. Buradan,
ANADOLU ÜNİVERSİTESİ
İÇ-ÇARPIM UZAYLARI
iz ( AB t ) =
n
n
i
j
221
∑ ∑ a ij btij
n
=∑
i
n
∑ a ij bij
= < A, B >
j
elde edilir.
1.8 Örnekteki A =
hesaplayalım.
1
2
3
4
, B =
2
0
1
-3
matrislerinin iz iç çarpımını
< A, B > = iz ( AB t )
t
AB =
1
2
2
1
3
4
0
-3
=
2
-5
6
-9
iz ( AB t ) = 2 - 9 = -7 = < A, B >
bulunur.
1.10. Tanım
V bir iç çarpım uzayı, x∈ V olsun. x vektörünün uzunluğu
x
= <x,x>
biçiminde tanımlanan bir sayıdır.
1.11. Örnek
R3 deki x = (1, 3, 5) vektörünün uzunluğunu hesaplayınız.
x
= < (1, 3, 5) , (1, 3, 5) >
= 1 + 9 + 25 = 35
1.12. Örnek
P2(R) deki p(x) = x2 + 1 vektörünün uzunluğunu hesaplayınız.
x
= < ( x2 + 1) , (x2 + 1) > =
=
1
(x4 + 2x2 + 1) dx
0
=
1 x5 + 2 x3 + x) 1
0
5
3
=
1 +2 + 1
5 3
=
28
15
AÇIKÖĞRETİM FAKÜLTESİ
1
0
2
(x2 + 1) dx
222
İÇ-ÇARPIM UZAYLARI
1.13. Teorem
Cauchy - Schwarz Eşitsizliği
V bir iç çarpım uzayı, x, y ∈ V olsun.
|< x, y >| ≤ ||x|| ||y||
dir.
Burada sol taraf bir gerçel sayının salt değerini, sağ taraf ise vektörlerin uzunlukları çarpımını verir.
Kanıt
x = 0 olması durumunda
|< x, y >| = 0
||x|| ||y||= 0
olduğundan eşitsizlik sağlanır.
x ≠ 0 olsun. Keyfi bir r ∈ R, r ≠ 0 için
< rx + y , rx + y > değerini alalım.
0 ≤ < rx + y , rx + y >
= < rx , rx + y > + < y , rx + y > tanımdan
= < rx , rx > + < rx, y > + < y , rx > + < y, y >
= r2 < x , x > + r < x , y > + r < x , y > + < y , y >
= r2 < x , x > + 2r < x , y > + < y , y >
olur. Burada a = < x , x >, b = 2 < x, y > , c = < y , y > ile gösterirsek
p (r) = ar2 + br + c ≥ 0
r ye göre ikinci dereceden polinom elde edilir. Bu polinomun bir parabol denklemi
olduğuna dikkat ediniz.
p (r) = ar2 + br + c
polinomunun r nin her değeri için
ar2 + br + c ≥ 0
olması için aşağıdaki iki koşuldan birinin sağlanması gerekir.
(i) ar2 + br + c = 0 ın gerçel köklerinin olmaması yani
b2 - 4ac < 0
olması,
ANADOLU ÜNİVERSİTESİ
İÇ-ÇARPIM UZAYLARI
223
y
r
(ii) ar2 + br + c = 0 ın iki katlı gerçel kökünün olmasıdır.
y
r
Uyarı: Eğer ar2 + br + c = 0 ın r1 ve r2 gibi farklı iki kökü olsaydı, a > 0 olduğu için r1 ve r2 kökleri arasında p(r) < 0 olurdu.
O halde
b2 - 4ac ≤ 0
olmalıdır. Buradan
b2 - 4ac ≤ 0
4 < x , y >2 ≤ 4 < x , x > < y , y >
< x , y >2 ≤ < x , x > < y , y >
ve böylece
|< x , y >| ≤ ||x|| ||y||
eşitsizliği elde edilir.
1.14. Örnek
Pn (R) de p(x) ve q(x) vektörleri için Cauch-Schwarz eşitsizliği
< p(x) , q(x) > 2 =
≤
=
dir. Bu eşitsizliği
AÇIKÖĞRETİM FAKÜLTESİ
1
0
p(x) , q(x) dx
1
0
p2 (x) dx
p(x)
2
2
1
0
q(x)
q2 (x) dx
2
224
İÇ-ÇARPIM UZAYLARI
p(x) = x + 1 ve q(x) = x2 - x - 1 vektörleri için doğrulayalım:
1
0
(x + 1) (x2 - x - 1)
2
dx ≤
1
0
1
x + 1 2 dx
0
2
x2 - x - 1 dx
işlemler yapılırsa,
1
0
x6 - 4x4 - 2x3 + 4x2 + 4x + 1 dx ≤
1
0
1
0
x2 2x + 1 dx
x4 - 2x3 - x2 + 2x + 1 dx
667 ≤ 287
210
90
eşitsizliğin doğruluğu sağlanır.
1.15. Teorem Üçgen Eşitsizliği
V bir iç çarpım uzayı, x, y ∈ V olsun.
||x + y|| ≤ ||x|| + ||y||
dir.
Kanıt
||x + y||2 =
=
=
=
≤
||x + y||2 ≤
<x+y,x+y>
<x, x+y> +<y, x+y>
< x , x > + < x, y > + < y , x > + < y, y >
<x,x> +2<x,y>+<y,y>
||x||2 + 2 ||x|| ||y|| + ||y||2 = ( ||x|| + ||y||)2
( ||x|| + ||y||)2
olur. Her iki tarafın pozitif karekökü alınırsa
||x + y|| ≤ ||x|| + ||y||
bulunur.
Bu eşitsizlik adını bir üçgenin bir kenarının uzunluğunun diğer iki kenarın uzunlukları toplamından küçük oluşundan almaktadır. Çünkü düzlemde kenarları
x, y, x + y vektörleri olan bir üçgende x + y nin uzunluğu x ve y nin uzunlukları
toplamından küçüktür.
x+
y
y
x
ANADOLU ÜNİVERSİTESİ
İÇ-ÇARPIM UZAYLARI
225
1.16. Tanım
V bir iç çarpım uzayı olsun.
x, y ∈ V , x, y ≠ 0 olmak üzere bu iki vektör arasındaki açı
cos θ =
< x, y >
x y
0 ≤θ ≤ π
eşitliği ile tanımlanır.
Cauchy - Schwarz eşitsizliğinden
| < x , y > | ≤ ||x|| ||y||
< x, y >
x y
≤ 1
buradan
-1 ≤
< x, y >
≤ 1
x y
böylece
-1 ≤ cos θ ≤ 1
olur. Buna göre herhangi bir çarpım uzayında sıfır olmayan iki vektör arasında yukarıdaki biçimde tanımlanan θ açısı anlamlıdır.
(1) eşitliğinden
< x , y > = ||x|| ||y||cos θ
yazabiliriz. Bu eşitlik R2 ve R3 deki x ve y vektörlerinin iç çarpımıdır. Böylece
cos θ =
< x, y >
x y
şeklinde ifade ettiğimiz açı kavramını herhangi bir iç çarpım uzayına genişletmiş
olduk.
1.17. Örnek
R3 deki x = (1, 0, 0) , y = (1, 1, 1) vektörleri arasındaki açıyı bulunuz.
Çözüm
cos θ =
< (1, 0, 0) , (1, 1, 0) >
1 + 0 + 0 . 12 + 12 + 02
2
2
2
cos θ = 1
2
AÇIKÖĞRETİM FAKÜLTESİ
= 1
2
226
İÇ-ÇARPIM UZAYLARI
buradan θ = π = 45°
4
bulunur.
1.18. Örnek
R2 (R) deki p(x) = 1 + x , q(x) = x vektörleri arasındaki açıyı bulunuz.
Çözüm
cos θ =
< p(x) , q(x) >
cos θ =
p(x)
q(x)
<1+x,x>
<1+x,1+x>
1
0
cos θ =
1
x 1 + x dx
1
1 + x 2 dx
0
<x,x>
0
5
6
=
5
= 6
1
7
3
3
7 .
3
x2 dx
cos θ = 5
2 7
olur.
1.19. Örnek
M 2x2 vektör uzayındaki A =
arasındaki açıyı bulunuz.
1
2
0
-1
, B=
Çözüm
AB t =
1
2
-1
2
0
-1
0
3
=
-1
8
0
-3
i z AB t = - 1 - 3 = - 4
i z AA t = i z
i z BB t = i z
cos θ =
-4
6
14
1
2
1
0
0
-1
2
-1
-1
0
-1
2
2
3
0
3
= -2
21
olarak bulunur.
ANADOLU ÜNİVERSİTESİ
=6
= 14
-1
0
2
3
vektörleri
İÇ-ÇARPIM UZAYLARI
2. Vektörlerin Ortogonalliği, Ortonormal Vektör
Kümeleri
(Gram-Schmidt ortonormalleştirme yöntemi)
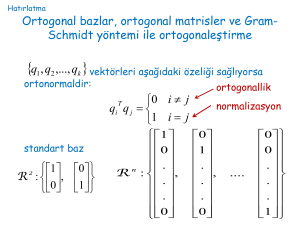
2.1. Tanım
V iç çarpım ve x, y ∈V olsun. Eğer < x, y > = 0 ise x ve y ye ortogonal (dik)
vektörler denir.
İki vektör arasındaki açı,
cos θ =
<x,y>
x y
ifadesinde
cos θ = 0
ise
x , y ortogonal vektörler,
cos θ = ± 1 yani < x, y > = ± ||x|| ||y|| ise x ve y vektörleri paralel vektörlerdir.
2.2. Örnek
R2 de x = (1, 3) , y = (- 3, 1) vektörleri için
< x, y > = < (1, 3) , (- 3, 1) > = 1. (- 3) + 3.1 = 0
olduğundan vektörler ortogonaldir.
2.3. Tanım
V bir iç çarpım uzayı. E ⊂ V olsun. E içindeki farklı her vektör çifti ortogonal ise E
ye ortogonal vektör kümesi denir. Ayrıca ortogonal E kümesindeki her vektörün
uzunluğu 1 ise E ye ortonormal bir küme denir.
2.4. Örnek
R3 teki x1 = (1, 0, 3) , x2 = (0, 2, 0) , x3 = (- 3, 0, 1) vektörlerinin ortogonal olduğunu gösteriniz. Ayrıca ortonormal kümeyi bulunuz.
AÇIKÖĞRETİM FAKÜLTESİ
227
228
İÇ-ÇARPIM UZAYLARI
Çözüm
< x1 , x2 > = < (1, 0, 3) , (0, 2, 0) > = 0
< x1, x3 > = < (1, 0, 3) , (- 3, 0, 1) > = 0
< x2 , x3 > = < (0, 2, 0) , (- 3, 0, 1) > = 0
O halde x1 , x2 , x3 vektörleri ortogonal vektörlerdir.
{ (x1 = (1, 0, 3) , x2 = (0, 2, 0) , x3 = (- 3, 0, 1) } kümesi de ortogonal kümedir.
x1 , x2 , x3 vektörlerinin birim vektörlerini bulalım.
x1 = < x1 , x1 > = < 1 , 0 , 3 , 1, 0, 3 > = 1 + 0 + 9 = 10
x1 = 1 1 , 0 , 3 =
10
1 ,0, 3
10
10
x1 ni birim vektörüdür.
Benzer şekilde,
x2 = 1 0 , 2 , 0 = 0 , 1 , 0 , x'3 = 1 - 3 , 0 , 1 = - 3 , 0 , 1
2
10
10
10
birim vektörlerdir.
1 ,0, 3
10
10
, 0,1,0 , -3 ,0, 1
10
10
kümesi ortonormal bir kümedir
2.5. Teorem
V n boyutlu iç çarpım uzayı olsun. V de sıfırdan farklı ortogonal vektörlerin
E = { x1 , x2 , ... , xn } kümesi lineer bağımsızdır.
Kanıt
E = { x1 , x2 , ... , xn } V içinde ortogonal bir küme olsun.
< xi , xj > = 0
i≠j
i , j = 1 , 2 , ... , n
dır. Şimdi
c1 x1 + c2 x2 + ... + cn xn = 0 ise , 1 ≤ i ≤ n için
< xi , 0 >
olduğundan
ANADOLU ÜNİVERSİTESİ
İÇ-ÇARPIM UZAYLARI
0 = < xi , c1 x1 + c2 x2 + ... + cn xn > = c1 < xi , x1 > + c2 < xi , x2 >... + ci < xi , xi >
+ cn < xi , xn >,
0 = c1 . 0 + c2 . 0 + ... + ci < xi , xi > + ... + cn.0
0 = ci < xi , xi >
elde edilir.
xi ≠ 0 olduğu için ci = 0 , i = 1 , 2 , ... , n . Buna göre E kümesi lineer bağımsızdır.
Sonuç
Sonlu boyutlu V iç çarpım uzayında ortonormal bir küme lineer bağımsızdır.
2.6. Tanım
V , n boyutlu bir vektör uzayı olsun. V de sıfırdan farklı x1 , x2 , ... , xn
vektörleri ortogonal ise bu vektörlerin kümesi V için bir ortogonal tabandır.
Eğer x1 , x2 , ... , xn vektörleri ortonormal ise bu vektörlerin kümesi V için bir
ortonormal tabandır.
2.7. Örnek
E = { (0 , 2 , 5) , (-2 , 1 , 0) , (1 , 0 , 1) } vektör kümesi R3 ün ortogonal bir tabanı mıdır?
Çözüm
Bir vektör uzayı için ortogonal taban olması demek tabandaki vektörlerin ortogonal olması demektir.
E = { (0 , 2 , 5) , (-2 , 1 , 0) , (1 , 0 , 1) }
kümesi R3 için bir tabandır (R3 te lineer bağımsız üç vektör). Bu tabanın ortogonal olup olmadığını araştıralım:
< (0 , 2 , 5) , (-2 , 1 , 0) > = 0 . (-2) + 2 . 1 + 5 . 0 = 2 ≠ 0
olduğu için E kümesi R3 ün bir ortogonal tabanı değildir.
2.8. Örnek
E = { x , 1 + x } kümesi P1 (R) nin ortogonal bir tabanı mıdır?
AÇIKÖĞRETİM FAKÜLTESİ
229
230
İÇ-ÇARPIM UZAYLARI
E kümesi P1 (R) için bir tabandır. Ortogonal taban olması için E nin ortogonal bir küme olması gerekir yani
<x,1+x>=0
olmalıdır.
1
1
0
0
< x , 1 + x > = x 1 + x dx =
= 1 x2 + 1 x3
2
3
1
0
x + x2 dx
=5 ≠0
6
olduğundan E kümesi P1 (R) nin ortogonal bir tabanı değildir.
2.9. Teorem
V , n boyutlu bir iç çarpım uzayı olsun. V nin bir E = { x1 , x2 , ... , xn } tabanı ortonormal bir tabana dönüştürülebilir.
Kanıt
Teoremin kanıtını vermeyeceğiz. Uygulamasını yapacağız.
Sonlu boyutlu V vektör uzayının, herhangi bir tabanından yararlanarak bir ortonormal tabanını bulmak için izlenen yönteme Gram - Schmidt ortonormalleştirme
yöntemi denir. E = { x1 , x2 , ... , xn } kümesi V nin herhangi bir tabanı ise E
kümesini, Gram - Schmidt ortonormalleştirme yöntemini kullanarak V için ortonormal bir taban bulalım:
E = { x1 , x2 , ... , xn } V nin bir tabanı olmak üzere
i)
y1 = x1 alalım.
ii) y n = xn - < xn , y 1 > y 1 - < xn , y 2 > y 2 - ... - < xn , y n - 1 > y n - 1
< y1 , y1 >
< y2 , y2 >
< yn - 1 , yn - 1 >
formülünden sırasıyla y2 , y3 , ... , yn vektörleri bulunur.
{ y1 , y2 , ... , yn }
kümesi V nin ortogonal bir tabanıdır.
iii) y1 , y2 , ... , yn vektörlerinin birim vektörleri sırasıyla
z1 , z2 , ... , zn ise
S = { z1 , z2 , ... , zn } kümesi V nin bir ortonormal tabanıdır.
ANADOLU ÜNİVERSİTESİ
İÇ-ÇARPIM UZAYLARI
231
2.10. Örnek
Gram-Schmidt ortonormalleştirme yöntemiyle R3 için bir ortonormal taban bulunuz.
Çözüm
R3 ün herhangi bir tabanını alalım:
E = { (1, 1, 1), (1, 0, 2), (1, 2, 3) } kümesi R3 için bir tabandır (Kontrol ediniz).
y1 = x1 = (1, 1, 1) alalım.
y 2 = x2 -
< x2 , y 1 >
< (1, 0, 2) , (1, 1, 1) >
y 1 = (1, 0, 2) (1, 1, 1)
< y1 , y1 >
< (1, 1, 1) , (1, 1, 1) >
y 2 = (1, 0, 2) - 3 (1, 1, 1) = (0, -1, 1)
3
y 3 = x3 -
< x3 , y 1 >
< x3 , y 2 >
y1 y2
< y1 , y1 >
< y2 , y2 >
= (1, 2, 3) -
< (1, 2, 3) , (1, 1, 1) >
< (1, 2, 3) , (0, -1, 1) >
(1, 1, 1) (0, -1, 1)
< (1, 1, 1) , (1, 1, 1) >
< (0, -1, 1) , (0, -1, 1) >
= (1, 2, 3) - 6 (1, 1, 1) - 1 (0, -1, 1)
3
2
= (1, 2, 3) - (2, 2, 2) - 0, -1 , 1 = 1 - 2 , 2 - 2 +1 , 3 - 2 - 1
2 2
2
2
= -1 , 1 , 1
2 2
Böylece,
kümesi R3 için ortogonal bir tabandır. Bu taba(1, 1, 1) , (0, -1, 1) , -1 , 1 , 1
2 2
nın bir ortonormal taban olması için her vektörün birim vektörü bulunur.
1 (1, 1, 1) , 1 (0, -1, 1) , 2 -1, 1 , 1
2 2
3
2
6
-1, 1 , 1
2 2
vektörleri sırasıyla (1, 1, 1) , (0, -1, 1) ,
vektörlerinin birim vektörleridir. Dolayısıyla
1 , 1 , 1 , 0, -1 , 1 , -2 , 1 , 1
3 3 3
2 2
6 6 6
kümesi R3 için bir ortonormal tabandır.
AÇIKÖĞRETİM FAKÜLTESİ
232
İÇ-ÇARPIM UZAYLARI
Siz de Gram-Schmidt ortonormalleştirme yöntemi ile P2 (R) için bir ortonormal
taban bulunuz.
2.11. Örnek
P1 (R) nin {1, 2 + x} tabanını kullanarak P1 (R) için bir ortonormal taban bulunuz.
Çözüm
{1, 2 + x} kümesi P1 (R) nin bir tabanı olduğuna göre
y1 = x1 = 1 alalım.
< x2 , y 1 >
y 2 = x2 y1
< y1 , y1 >
=2+x-
<2+x,1>
1
<1,1>
1
=2+x-
0
(2 + x) dx
1
0
dx
5
=2+x- 2
1
= 2 + x -5 = - 1 + x
2
2
1, - 1 + x kümesi ortogonal bir tabandır.
2
- 1 + x vektörünün birim vektörünü bulalım.
2
-1 +x =
2
< - 1 + x , -1 + x > =
2
2
1
0
2
- 1 + x dx =
2
-1 +x
2
= - 3 + 2 3x
1
12
1, - 3 + 2 3 x
kümesi ortonormal bir tabandır.
ANADOLU ÜNİVERSİTESİ
1 = 1
12
12
İÇ-ÇARPIM UZAYLARI
233
Değerlendirme Soruları
1.
R4 deki (1, 4, 5, -3) vektörünün uzunluğu aşağıdakilerden hangisidir?
A.
7
D. 7
2.
B.
60
C.
E.
20
P2 (R) de tanımlı iç çarpıma göre p(x) = x2 + 3x vektörünün uzunluğu
aşağıdakilerden hangisidir?
A.
47
10
B.
3
D.
1
4
E.
7
C.
3. M2x2 de tanımlı iç çarpımına göre
ğıdakilerden hangisidir?
4.
A. 10
B. 20
D.
E.
40
1
2
3
4
47
vektörünün uzunluğu aşa-
C.
30
17
R3 deki (1, 3, 5) (-1, 4, 7) vektörleri arasındaki açının kosinüsü aşağıdakilerden hangisidir?
40
35 66
46
D.
66
A.
5.
51
B.
1
E.
35 66
46
35 66
C. 46
35
P2 (R) de tanımlı iç çarpıma göre p(x) = 2, q(x) = 1 + x2 vektörleri arasındaki açının kosünüsü aşağıdakilerden hangisidir?
A. 2 15
3 7
B.
15
7
D. 2 15
7
E.
15
3 7
AÇIKÖĞRETİM FAKÜLTESİ
C. 3 7
15
234
İÇ-ÇARPIM UZAYLARI
6.
Aşağıdaki kümelerden hangisi ortogonaldir?
A. { (1, 2, 1), (1, -1, 1), (1, 0, -1) }
B. { (1, 2, 1), (3, 4, 5), (1, 0, 0)}
C. { (2, 2, -1), (2, -1, 2), (1, 0, 0) }
D. { (1, 1, 3), (0, 1, 3), (2, 0, 1)}
E. { (1, 0, 0), (0, 1,0), (0, 0, 1) (1, 1, 1) }
7.
P2 (R) de aşağıdaki kümelerden hangisi ortogonaldir?
A. { 1, 3, 1 + x + x2 }
B. { 1, x, x2, 2x2 + n }
2
C. { 1, 1 - x, 1 - x }
2
3
D. { 1, x - 1 , x2 - x + 1
2
6
E. { 1, x }
8.
R3 nin V = { (x, y, z) | x + y + z = 0, x, y, z ∈ R } alt uzayının ortogonal
tabanı aşağıdakilerden hangisidir?
A.
1 , -1, 1 , -2, 1, 1
2
2
B. { (1, 1, -2) , (1, -1, 0) }
C. { ( 1, 1, 1) , (0, 0, 1) }
E.
9.
D. { ( 1, 0, 1) , (0, 1, 0 ) }
1 , 1 , 1 , (1, 1, 1)
2 3 4
R2 için aşağıdakilerden hangisi bir ortonormal tabandır?
A. { (1, 0), (1, 1) }
B. { (1, 0), (0, 1) }
C. { (1, 1), (2, 2) }
D. { (0, 0), (1, 3) }
E. { (-4, 5), (1, 1), (-1, 0) }
Değerlendirme Sorularının Yanıtları
1. C
2. A
3. C
4. E
ANADOLU ÜNİVERSİTESİ
5. A
6. A
7. D
8. B
9. B