3. SÜREKLİLİK 3. SÜREKLİLİK )32(lim + x , , gibi limitleri

DERS:
ÜNİTE:
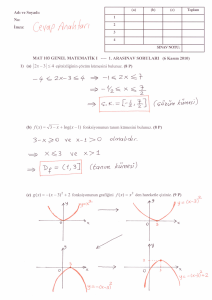
KONU:
MATEMATİK I
LİMİT ve SÜREKLİLİK
MAT101(08)
3. SÜREKLİLİK
3. SÜREKLİLİK
lim (2 x + 3) , lim 12 , limπ sin x gibi limitleri hesaplamak için limiti aranan fonksiyonlarda x
x→5 x
x →0
x→ 2
yerine sırasıyla 0, 5,
π
2
yazılması yeterli idi. Ancak aynı yöntem her fonksiyonun limitinde
geçerli değildir, örneğin lim x2 − 5 limitinde bu yöntem çalışmaz. Acaba hangi durumlarda
x →5 x − 25
lim f ( x) limiti hesaplarken x yerine a yazılarak limit kolayca hesaplanabilir?. Bunun için
x→ a
fonksiyon hangi özelliğe sahip olmalıdır? Bu soruların cevabı, fonksiyonun x = a daki
sürekliliği olacaktır.
Tanım: A ⊆ R , f : A → R bir fonksiyon ve a ∈ A olsun.
lim f ( x) = f (a)
x →a
ise f fonksiyonu
a noktasında süreklidir denir. Eğer f fonksiyonu A kümesinin her
noktasında sürekli ise fonksiyon A üzerinde süreklidir denir.
y
y
y
y = f (x)
y = g (x)
L2
g(a)
L1
L1
h(a)=L1
x
x
x
a
a
a
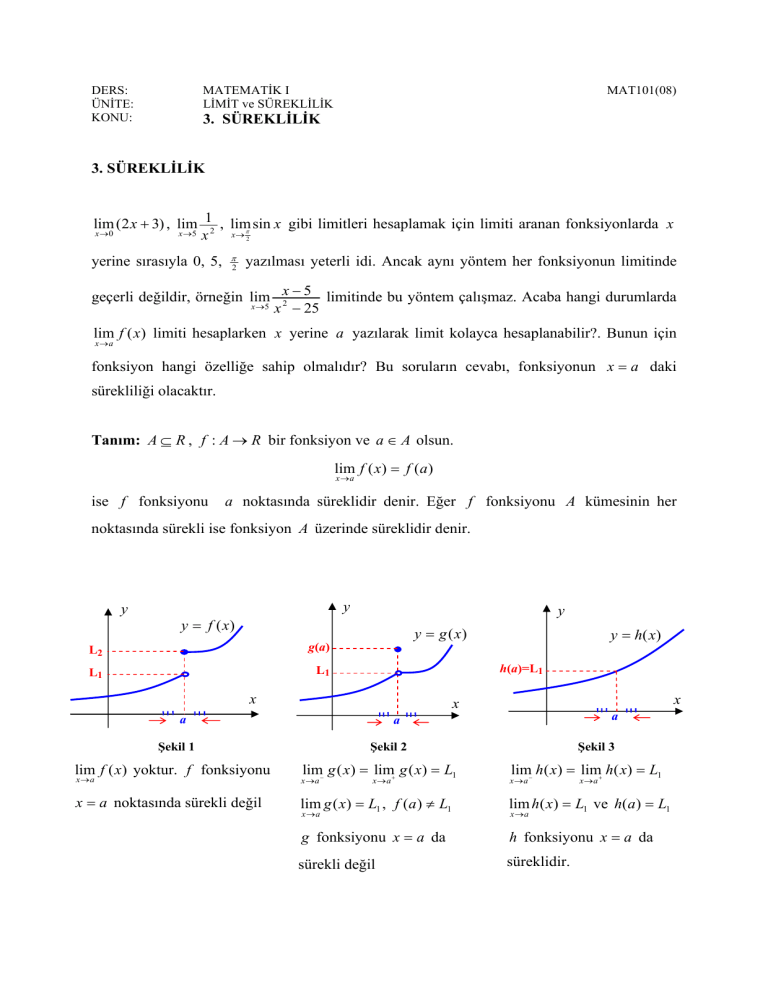
Şekil 1
lim f ( x) yoktur. f fonksiyonu
y = h( x )
Şekil 2
lim g ( x) = lim+ g ( x) = L1
Şekil 3
lim h( x) = lim+ h( x) = L1
x→ a
x→a −
x = a noktasında sürekli değil
lim g ( x) = L1 , f (a ) ≠ L1
lim h( x) = L1 ve h(a ) = L1
g fonksiyonu x = a da
h fonksiyonu x = a da
sürekli değil
süreklidir.
x→a
x →a
x→a −
x→a
x →a
Örnek 1. f : R → R ,
⎧− x 2 , x < 0
⎪
f ( x) = ⎨ 0 , x = 0
⎪ x + 1, x + 1
⎩
fonksiyonunun x = 0 daki sürekliliğini inceleyiniz.
Örnek 2. g : R → R , g ( x) = 2 [| x |] − x 2 fonksiyonu R üzerinde sürekli midir?
Örnek 3. s : R → R , s ( x) = sgn( x 2 ) fonksiyonunun süreksiz olduğu noktaları tespit ediniz.
Örnek 4. h : R → R ,
⎧5 x − 3, x ≥ 2
h( x ) = ⎨
⎩ ax + 1 x < 2
fonksiyonunun x = 0 da sürekli olması için a ne olmalıdır?
Örnek 5. k : R → R ,
⎧ x+3 ,
x≥2
⎪ x2 − 9
⎪
k ( x) = ⎨
⎪2 x + 1 , x < 2
⎪⎩
x+5
fonksiyonunun süreksiz olduğu noktaları tespit ederek sürekli olduğu kümeyi yazınız.
Örnek 6. f ( x) = [| x |] + [| − x |] fonksiyonunun grafiğini çiziniz. Fonksiyon hangi noktalarda
süreksizdir.
Örnek 7. f ( x) = tan x ile tanımlı f fonksiyonunun süreksiz olduğu noktaları bulunuz.
Örnek 8.
⎧ x2 − 4
, x≠2
⎪
⎪ x−2
g ( x) = ⎨
⎪ m,
x=2
⎪
⎩
fonksiyonunun her yerde sürekli olması için m = ?
2
Bir fonksiyon bir a noktasında süreksiz ise şu durumlardan birisi söz konusudur:
1. lim f ( x) limiti mevcut ancak bu limit değeri f (a ) dan farklı veya fonksiyon bu noktada
x→ a
tanımlı olmayabilir. Bu tip süreksizliğe kaldırılabilir süreksizlik denir. Örneğin Şekil 2
de grafiği verilen g fonksiyonunun x = a daki süreksizliği ve Örnek 3 de verilen s
fonksiyonunun x = 0 daki süreksizliğidir.
2. a noktasındaki sağ ve sol limitleri mevcut ancak farklı olabilir. Bu tip süreksizliğe
sıçrama süreksizliği denir. Örneğin Şekil 1 de grafiği verilen f fonksiyonunun x = a
daki süreksizliği ve Örnek 1 de verilen f fonksiyonunun x = 0 daki süreksizliği, sıçrama
süreksizliğidir.
3. Sağ veya sol limitlerden en az biri m ∞ veya mevcut olmayabilir. Bu tip süreksizliğe
sonsuz süreksizlik denir.
fonksiyonunun x =
π
2
R − { (2k + 1) π2 : k ∈ R } den
R ye tanımlanan
tan x
deki süreksizliğidir.
Tanım: A ⊆ R , f : A → R bir fonksiyon ve a ∈ A olsun.
1) lim+ f ( x) = f (a) ⇔ f fonksiyonu sağdan süreklidir.
x →a
2) lim− f ( x) = f (a) ⇔ f fonksiyonu soldan süreklidir.
x→a
Örnek 9.
⎧− x + 1 , x < 0
⎪
f ( x) = ⎨
⎪ x −1 , x > 0
⎩
fonksiyonunu x = 0 da tanımlı değildir.
a) f fonksiyonunun x = 0 da sağdan sürekli olması için f (0) = ?
b) f fonksiyonunun x = 0 da soldan sürekli olması için f (0) = ?
Teorem: A ⊆ R , f : A → R ve g : A → R fonksiyonları, a ∈ A noktasında sürekli ve a ∈ R
ise | f |, f 2 , c. f , f m g , f ⋅ g fonksiyonları da a noktasında süreklidir. Ayrıca g (a) ≠ 0 ise
f
fonksiyonu da a da süreklidir.
g
3
Örnek 10. Bir polinom fonksiyon R üzerinde sürekli midir?
Örnek 11. Bir rasyonel fonksiyonun süreksiz olduğu noktaları nasıl tespit edebiliriz?
Örnek 12. Trigonometrik fonksiyonların sürekli oldukları kümeleri sırasıyla tespit ediniz.
Örnek 13. Logaritmik ve üstel fonksiyonların sürekli oldukları kümeleri tespit ediniz.
Örnek 14. Hiperbolik fonksiyonların sürekli oldukları kümeleri sırasıyla tespit ediniz.
Teorem: f : A → B ve g : B → C fonksiyonları verilmiş olsun. f fonksiyonu a noktasında,
g fonksiyonu f (a) da sürekli ise gof fonksiyonu da a noktasında süreklidir
Örnek 15. f ( x) = 1 ve g ( x) = 2 1
ile tanımlı f ve g fonksiyonları veriliyor.
x −1
x + x−2
gof fonksiyonunun süreksizlik noktalarının kümesini bulunuz.
Kapalı Bir Aralıkta Sürekli Fonksiyonların Özellikleri
Teorem: (Ara Değer Teoremi)
f fonksiyonu [a, b] kapalı aralığında sürekli olsun. f (a ) ile f (b) değerleri arasında bir d
seçilsin. O halde f (c) = d olacak şekilde [a, b] aralığında en az bir c vardır.
y
y = f (x)
f(b)
f(c) = d
f(a)
x
a
c
b
4
Teorem: (Balzano Teoremi)
f fonksiyonu [a, b] aralığında sürekli ve f (a ) ile f (b) zıt işaretli ise a ile b arasında
f (c) = 0 olacak şekilde en az bir c vardır.
y
y = f (x)
f(b)
0
f(a)
x
a
c
b
Örnek 16. x3 + x 2 − 1 = 0 denkleminin 0 ile 1 arasında bir kökü olduğunu gösteriniz.
Örnek 17. f ( x) =
1
fonksiyonu için f (−1) = −1 , f (1) = 1 dir. Fonksiyon − 1 ile 1 arasında
x
sıfır değerini alır mı? Bu sonuç Balzano teoremi ile çelişir mi?
Teorem: f fonksiyonu f : [a, b] → R fonksiyonu sürekli ise sınırlıdır.
y
Yerel Maks. Nokta ve
Mutlak Maks Nokta
f(c)
Y. Maks. Nokta
Y. Maks. Nokta
f(a)
x
b
a
Yerel Min. Nokta
f(b)
0
c
y = f (x)
Yerel Min. Nokta
f fonksiyonu x = a noktasında bir yerel maksimuma sahiptir. f (a) ‘ya f nin yerel
maksimum değeri denir. Yerel maksimum ve yerel minimum değerlerinin hepsine birden f
fonksiyonunun ekstremumları veya ekstremum değerleri denir.
5
Örnek 16.
− 3 ≤ x < −1
⎧ − x,
⎪
1≤ x < 0
f ( x) = ⎨ x + 2 ,
⎪2( x − 1) 2 ,
0≤ x≤3
⎩
ile tanımlanan fonksiyonun ekstremum
değerlerini bulunuz.
Teorem: f : [a, b] → R sürekli ve kesin artan bir fonksiyon, f (a) = c ve f (b) = d olsun.
1) f : [a, b] → [c, d ] fonksiyonunun f −1 : [c, d ] → [a, b] tersi vardır.
2) f −1 , [c, d ] üzerinde kesin artandır.
3) f −1 , [c, d ] üzerinde süreklidir.
ÖDEVLER
M. BALCI, Genel Matematik Cilt I
Sayfa 108-112 problemler
C.H. EDWARDS, D.E. PENNY, Matematik Analiz ve Geometri Cilt I
Sayfa 94-95 problemler
Sayfa 96-97 problemler
Sayfa 95-96 2.4. Proje: Kırık Ağaç (Tekrar)
KAYNAKLAR
M. BALCI, Genel Matematik Cilt I, Balcı Yayınları, Ankara, 2003.
C.H. EDWARDS, D.E. PENNY, Matematik Analiz ve Geometri Cilt I, (çev.ed. Ömer AKIN), Palme Y., Ankara, 2001.
6