Sample Questions

21931 STA201E Statics
Sample Questions 1
Problem 1:
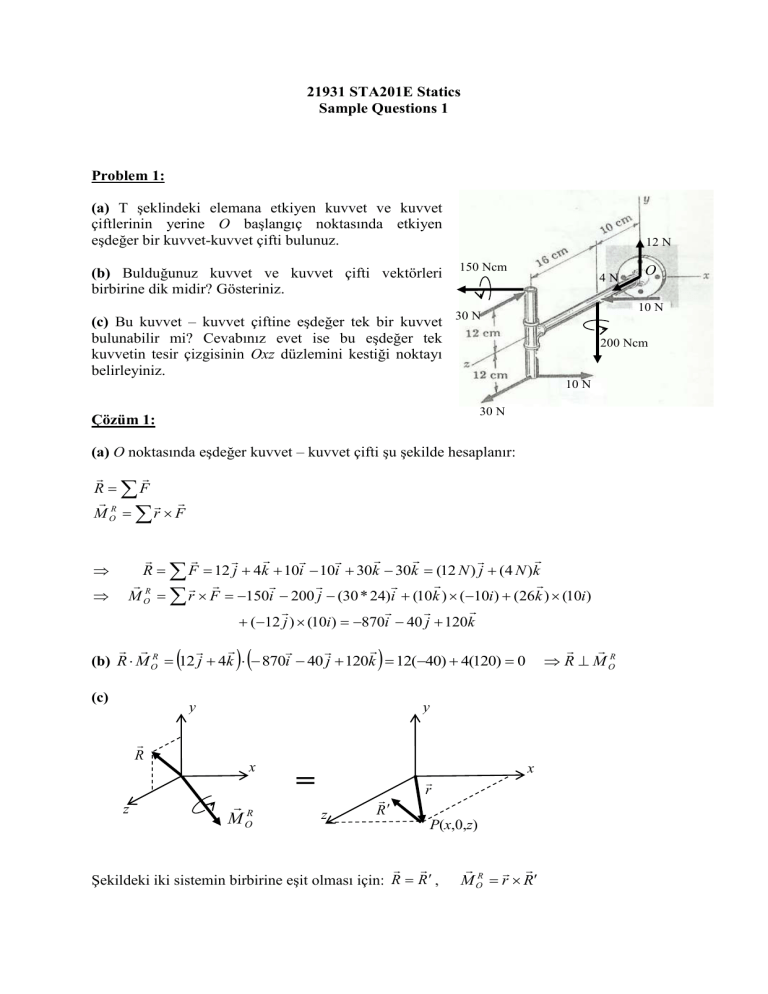
(a) T şeklindeki elemana etkiyen kuvvet ve kuvvet
çiftlerinin yerine O başlangıç noktasında etkiyen
eşdeğer bir kuvvet-kuvvet çifti bulunuz.
(b) Bulduğunuz kuvvet ve kuvvet çifti vektörleri
birbirine dik midir? Gösteriniz.
(c) Bu kuvvet – kuvvet çiftine eşdeğer tek bir kuvvet
bulunabilir mi? Cevabınız evet ise bu eşdeğer tek
kuvvetin tesir çizgisinin Oxz düzlemini kestiği noktayı
belirleyiniz.
12 N
150 Ncm
4N
10 N
30 N
200 Ncm
10 N
30 N
Çözüm 1:
(a) O noktasında eşdeğer kuvvet – kuvvet çifti şu şekilde hesaplanır:


R  F

 
M OR   r  F












R   F  12 j  4k  10i  10i  30k  30k  (12 N ) j  (4 N )k






 
M OR   r  F  150i  200 j  (30 * 24)i  (10k )  (10i)  (26k )  (10i)




 (12 j )  (10i)  870i  40 j  120k





 



(b) R  M OR  12 j  4k   870i  40 j  120k  12(40)  4(120)  0
(c)
y

R
z


 R  M OR
y
x

M OR
=
z

R
x

r
P(x,0,z)
 
Şekildeki iki sistemin birbirine eşit olması için: R  R  ,
O

 
M OR  r  R



 R   (12 N ) j  (4 N )k
  









 870i  40 j  120k  r  R   ( xi  zk )  (12 j  4k )  (12 z )i  (4 x) j  (12 x)k
 870  12 z

  40  4 x
 120  12 x


x  10 cm
z  72.5 cm
Problem 2: Üç boyutlu kartezyen eksen takımında bir vektörün x, y ve z eksenleriyle yaptığı
açılar sırasıyla θx, θy ve θz olsun. Bu durumda θx = θy = 30° olup olamayacağını gösteriniz.
Çözüm 2:
2
2
 3  3
1
 
    olamaz
cos  x  cos  y  cos  z  1  cos  z  1  



2
 2   2 
2
2
2
2
Problem 3: 600 N ağırlığında bir blok AC ve BC
kablolarına asılmıştır.
(a) α açısının hangi değeri için AC
kablosundaki kuvvet minimum olur?
(b) α açısının bu değeri için AC ve BC
iplerindeki kuvvetleri hesaplayınız.
α=?
Çözüm 3:
(a) β=90° için TAC minimum olur.
→ α=40°
α 
TCA
β
600 N
40°
(b)
TCB
B
A

TCB
TCA
T
600
 CB 
 TCA  385.6 N
sin 40 sin 50 sin 90
 459.6 N
50°
C
W = 600 N
Problom 4: Sürtünmesiz çubuklar üzerinde bulunan A ve B
bilezikleri 25 cm uzunluğunda bir tel ile birbirine bağlanmıştır.
Teldeki kuvvetin şiddeti 125 N ise x=9 cm için telin B
bileziğine
uyguladığı
kuvvetin
skaler
bileşenlerini
hesaplayınız.

P
cm

Q

 

Çözüm 4: rBA  BA  9i  20 j  zk

P
BA  9 2  20 2  ( z) 2  25  z  12 cm




rBA  BA  9i  20 j  12k
Tx T y
T
125

 z 
 Tx  45 N , T y  100 N , Tz  60 N
9 20  12 25

Q

TBA
cm




TBA  (45 N )i  (100 N ) j  (60 N )k

Problem 5: Şiddeti 50 N olan bir P kuvveti, aşağıdaki şekilde kenar uzunlukları verilen

dikdörtgenler prizmasına etkimektedir. P kuvvetinin D göre momentini hesaplayınız.
y
G
F
E
D
O
A
z
16 cm

P
C
x
12 cm
B
15 cm
y


Çözüm 5: P  P P  50


rDF  rF / D


 16 j  12k


 (40 N ) j  (30 N )k
(16) 2  (12) 2




 
 rF  rD  15i  16 j  (16 j  12k )


 15i  12k

rDF
G
D
F
E
O
A
z
15 cm
16 cm

P
C
B
x
12 cm

i



M D  rDF  P  15

j

k
0
 12
0  40 30




 M D  480i  450 j  600k Ncm
Problem 6: AB elemanına tesir eden 260 N luk
kuvvetin A noktasına göre,
(a) moment vektörünü bulunuz.
(b) Bulduğunuz moment vektörünün yönünü
belirtiniz. (kağıt düzlemine göre hangi yönde?)
(c) Bu moment vektörünün şiddetini belirtiniz.
40 cm
C
A
66 cm
Çözüm 6:
(a) BC 
30 cm
y
962  402


 F cos i
 104 cm
Skaler büyüklükler cinsinden hesap yapılarak
+
B
260 N


M A  F cos  (40 cm)  F sin  (30 cm)
C
 (260 N ) * (96 / 104)( 40 cm)  (260 N ) * (40 / 104)(30 cm)
α
B


 F sin j
260 N
A
66 cm
40 cm
x
30 cm
 6600 Ncm  66 Nm
elde edilir. Veya vektörel hesap yapılarak








M A  rB  F  (30i  40 j )  (260 cos  i  260 sin  j )  (6600 Ncm)k

aynı sonuca ulaşılır. F vektörü C noktasına kaydırılarak A noktasına göre moment daha kolay
bulunabilir.
y
B


 F cos i
C
α
40 cm
A
x


 F sin j
260 N
66 cm
+
30 cm

M A  F sin  (30 cm)  (260 N ) * (40 / 104)(66 cm)  6600 Ncm  66 Nm
(b) Moment vektörünün yönü kağıt düzleminden dışarı doğrudur. Çünkü saat ibreleriyle ters
istikamette döndürme etkisine sahiptir.
(c) Momentin şiddeti 6600 Ncm dir.

P
Problem 7: Şekildeki konsol kiriş P  100 N ve Q  200 N
şiddetindeki iki kuvvetin etkisindedir.
(a) Kiriş ait serbest cisim diyagarmını çiziniz.
(b) Kiriş tam bağlı mı? Açıklayınız.
(c) Mesnet tepkilerini hesaplayınız.

Q
2m
2m
Çözüm 7: (a)

Ax
100 N

M

Ay
2m
(b) Kiriş tam bağlıdır. Çünkü mesnet tepkisi sayısı denge
denklemi sayısına eşittir ve genel yükleme halinde bütün
denge denklemleri sağlanır. (Yani genel yüklemeyi
dengeleyecek mesnet tepkileri oluşur)
200 N
2m
(c) Fx  0 : Ax  0
Fy  0 : Ay  200  100  0  Ay  100  Ay  100 kN 


( ya da Ay  100 j )
+ M A  0:  200 * 2  100 * 4  M  0  M  0
Problem 8: Şekildeki ABDE çubuğu A ve E
noktalarında küresel mafsal ve D noktasına
bağlı DF ipi ile mesnetlenmiştir.
(a) ABDE çubuğunun
diyagramını çiziniz.
serbest
cisim
(b) DF ipindeki kuvvetin şiddetini
hesaplayınız. (İpucu: AE eksenine göre
moment alınız)
Çözüm 8: Aşağıdaki şekilde ABDE çubuğuna ait serbest cisim diyagramı verilmiştir. Rijit bir
cisim dengede ise bu cisme tesir eden bütün kuvvetlerin (mesnet tepkileri dahil) seçilen
herhangi bir noktaya göre momentinin sıfır olması gerekir. Yine seçilen herhangi bir eksene
göre de momentin sıfır olması gerekir. Bu düşünceden hareketle ipucunda belirtildiği üzere
AE eksenine göre toplam moment ifadesini yazalım. Açıktır ki A ve noktalarındaki mesnet
tepkilerinin AE eksenine gore momenti sıfırdır çünkü etki noktaları bu eksen üzerinde yer
almaktadır (tesir çizgilerinin aynı ekseni kesmesi/paralel olması da momentlerinin o eksene
gore sıfır olması için yeterlidir). O halde sadece 600 N luk dış yükün ve ipteki T kuvvetinin
AE eksenine gore momenti sıfırdan farklı olacaktır. AE eksenine göre moment, E noktasına
göre alınan momentin AE ekseni üzerindeki izdüşümü olarak hesaplanabilir.

Ay

Az

Ey

Ex

T

rED

Ez

Ax

rEC






 160i  110 j  80k
T  T DF  T 
 (160) 2  (110) 2  ( 80) 2
 16  11  8  
 T  i 
j  k
21
21 
 21

 


M E  rED  T  rEC  (600 j )



i
j k

 T


T
rED  T 
16 0 0 
128 j  176k
21
21
 16 11  8





rEC  (160mm)i  (140mm)k


rED  (160mm)i




rAE
 70i  240k
 AE   
rAE
(70) 2  (240) 2
7  24 
 i 
k
25
25









rEC  (600 j )  16i  14k  (600 j )  (9600 Ncm)k  (8400 Ncm)i







T
M E 
128 j  176k  (9600 Ncm)k  (8400 Ncm)i 
21
 T
 T

 (8400 Ncm)i  128 j   176  9600 k
21
 21



 T
 T
 7  24   
 
M AE   AE  M E    i 
k     (8400 Ncm)i  128 j   176  9600 k 
25  
21
 25
 21
 

7
24  T

8400   176  9600   0
25
25  21

T  853,12 N bulunur.


