KONUNUN AŞAMALARI
KAPALI ARALIĞIN PARÇALANMASI
BELİRLİ İNTEGRAL VE İNTEGRALLENEBİLİR
FONKSİYON
BELİRLİ İNTEGRALİN ÖZELLİKLERİ
KAPALI ARALIĞIN PARÇALANMASI
a
b
x0 < x1<x2<x3<......<xk-1<xk<.......<xn-1<xn
P={x0 ,x1,x2,x3,......,xk-1,xk, ......., xn-1,xn }
[a,b] aralığının bir parçalanması (bölüntüsü)
Her bir [xk-1, xk] kapalı alt aralığı için;
xk= xk –xk-1 sayısı
[xk-1, xk] kapalı alt aralığının uzunluğu
x1= x1 –x0
x2= x2 –x1
x3= x3 –x2
....................
Alt aralıkların
uzunlukları olmak
üzere
xn= xn –xn-1
[a.b] aralığının uzunluğu
b-a = x1+ x2+ x3+..........+ xn
x1= x1 –x0
x2= x2 –x1
x3= x3 –x2
....................
Alt aralıklarının
uzunlukları
birbirine eşitse
xn= xn –xn-1
P bölüntüsüne
[a,b] aralığının DÜZGÜN BÖLÜNTÜSÜ denir.
P düzgün bir bölüntü ise;
[a,b] aralığını, n eşit parçaya bölen P bölüntüsünün herhangi bir alt aralığının uzunluğu, P bölüntüsünün normunu (aralık genişliğini) verir.
ba
xk=
= P
n
ÖRNEK:
[2,7] ARALIĞI İÇİN
P={2,11/3,16/3,7} bölüntüsü, düzgün bir
bölüntüdür.
11
5
2
x1=
3
3
16 11 5
x2=
3 3 3
72 5
P
3
3
16 5
x3= 7
3 3
y
y=f(x)
m1 m2
m3
x1 x2 x3
m4
xk
mn
xn
a=x0 x1 x2 x3.......xk-1 xk ..........xn-1 xn=b x
0
ALT TOPLAM
n
A(f , P ) m k .Δxk m1 .Δx1 m2 .Δx2 ...... mn .Δxn
k 1
y
y=f(x)
M1 M 2
M3
x1 x2 x3
MK Mn
xk
xn
a=x0 x1 x2 x3.......xk-1 xk ..........xn-1 xn=b x
0
ÜST TOPLAM
n
Ü(f , P) M k .Δxk M1 .Δx1 M2 .Δx2 ...... Mn .Δxn
k 1
y
y=f(x)
f(t1) f(t2)
0
f(tk)
a=x0 t1 x1 t2 x2 xk-1 tk xk xn-1 tn xn
x1
x
x
2
k
RİEMANN
TOPLAMI
n
f(tn)
x
x
n
R(f , P ) f ( t k ).Δxk f (t1 ).Δx1 f (t 2 ).Δx2 ...... f (tn ).Δxn
k 1
Bu toplamlar arasındaki sıralama
n
m
k 1
n
n
k .Δx k
Alt Toplam
f (t
k 1
k
).Δxk
Rieman Toplamı
M
k 1
k
.Δxk
Üst Toplam
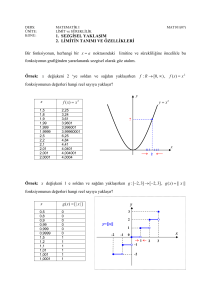
ÖRNEK:
f:[0,2] R, f(x)=x2 fonksiyonu için;
[0,2] aralığını, 4 eşit parçaya bölerek;
Alt toplamını
Üst toplamını
Riemann toplamını bulalım:
P, düzgün bir bölüntü olduğundan
ba 20 1
x1= x2= x3= x4=
4
4
2
P={0, 1/2 , 1 , 3/2 , 2}
Alt toplamı
n
A(f , P )
y
m
k 1
k
.Δx k
y=x2
0
1/2 1
3/2 2
x
m1=f(0)=0
m2=f(1/2)=1/4
m3=f(1)=1
m4=f(3/2)=9/4
n
A(f , P ) m k .Δxk m1 .Δx1 m2 .Δx2 m3 .Δx3 m4 .Δx4
k 1
7
1 1 1
1 9 1
0 1
4
2 4 2
2 4 2
Üst toplamı
n
Ü(f , P) Mk .Δx k
y
k 1
y=x2
M1=f(1/2)=1/4
0
1/2 1
3/2 2
x
M3=f(3/2)=9/4
n
M2=f(1)=1/4
M4=f(2)=4
Ü(f , P) Mk .Δx k M1 .Δx 1 M2 .Δx 2 M3 .Δx 3 M4 .Δx 4
k 1
15
1 1
1 9 1
1
1 4
4
4 2
2 4 2
2
Riemann toplamı:
n
R(f , P) f (t k ).Δx k
y
k 1
y=x2
1/2
0
1
4
t1
1
21
2
4
0
1
3
4
3/2
5
4
2
x k 1 x k
f (t k )
2
x
7
4
1
1
3
t2 2
2
4
t3
3
2 5
2
4
1
3
2
7
t4 2
2
4
n
Ü(f , P) Mk .Δx k M1 .Δx 1 M2 .Δx 2 M3 .Δx 3 M4 .Δx 4
k 1
1
3
5
7
Ü(f , P) f ( ). Δ 1 f ( ). Δx 2 f ( ). Δx 3 f ( ). Δx 4
4
4
4
4
1 1 9 1 25 1 49 1
16 2 16 2 16 2 16 2
21
8
f:[a,b] R sınırlı bir fonksiyon ve [a,b] aralığının bir
bölüntüsü P olsun.
lim A(f , P) lim Ü(f , P) s
P 0
P 0
ise, f fonksiyonu, [a,b] aralığında İNTEGRALLENEBİLİR FONKSİYONDUR. Bu “s” sayısına da, f fonksiyonunun [a,b] aralığındaki BELİRLİ İNTEGRALİ denir.
b
f (x ).dx s
a
P 0 olması ne demektir?
[a,b] aralığının, [xk-1,xk] alt aralıklarının uzunluklarının SIFIRA yaklaşması demektir.
Bu durumda, alt ve üst toplamlarda elde edilen dikdörtgenlerin taban uzunlukları küçülecek ve dolayısı
ile, alt ve üst toplam birbirine yaklaşacaktır.
P parçalanması, düzgün bir
parçalanma olduğundan;
P 0 n
b
lim f (t k ). Δx k f (x ).dx
n
k 1
a
n
ÖRNEK:
3
2
x
dx belirli integralini, tanıma göre hesaplayalım:
0
[0,3] aralığını, n eşit parçaya bölersek;
k{0,1,2,....,n} için,
ba 30 3
P Δx k
n
n
n
t k a k.Δx k olarak seçilirse;
3 3k
tk 0 k .
n
n
3
n
3k 3
2
f (
).
0 x dx lim
P
n n
k 1
n 9k 2 3
27 n 2
lim 2 lim 3 k
P
n P n k 1
k 1 n
27 n.(n 1).(2n 1)
lim 3
P 0 n
6
27.(2n3 3n2 n)
lim
3
n
6n
27.2
9
6
3
x
0
2
dx 9
İNTEGRAL HESABIN TEMEL TEOREMİ
f: [a,b] R fonksiyonu, [a,b] aralığında integrallenebilen bir fonksiyon olsun. F:[a,b] R fonksiyonu
(a,b) aralığında türevli ve x(a,b) için, F’(x)=f(x)
ise,
b
f (x)dx F(x)
a
b
a
F(b) F(a) dır .
ÖRNEK:
2
(3x 4)dx
belirli int egralini bulalım :
1
3x 2
(3x 4)dx 2 4x c
3.2 2
F( 2 )
4.2 14
2
2
3.12
11
F(1)
4.1
2
2
11 17
1 (3x 4)dx F(2) F(1) 14 2 2
f ve g fonksiyonları, [a,b] aralığında integrallenebilir iki fonksiyon ve a,b,c R ise;
b
b
b
a
a
a
[f (x) g( x)]dx f (x)dx g(x)dx
π
π
π
π /2
π /2
π /2
(3. sin x cos x)dx = 3. sin xdx + cos xdx
=
3(-cosx) +
sinx
3(-cosx) +
-3.[(cos - cos(/2)] +
sinx
[sin - sin (/2)]
[-3.((-1)+3.0)] + (0-1)
2
b
c. f ( x)dx
a
b
c. f ( x)dx
a
8
8
3
3
4.ln x.dx 4. ln x.dx
5
5
1
1
3
3
5
.
x
.
dx
5
.
x
.dx
6
2
3 .dx
x
6
dx
3 .
x
2
a
f ( x)dx
0
a
3
ln x.dx 0
3
1
3
x
.dx 0
1
2
dx
2 x 0
b
f ( x)dx
a
a
f ( x)dx
b
5
1
1
5
2
2
3
x
dx
3
x
dx
x3
3.
3
5
5 3 13 125 1 124
1
x3
3.
3
1
5
(13 5 3 ) (1 125) (124) 124
[a,c] aralığında integrallenebilir bir f
fonksiyonu için, a<b<c ise;
c
f (x)dx
a
b
f ( x )dx
a
c
f (x)dx
b