İKİ DEĞİŞKENLİ OLASILIK Rassal bir deneme yapılmakta

İKİ DEĞİŞKENLİ OLASILIK
Rassal bir deneme yapılmakta ve farklı iki olay ile ilgilenilmektedir.
A1, A2,…,Ai olayları bağdaşmaz ve bütünü kapsayıcıdır.
B1, B2,…,Bj olayları bağdaşmaz ve bütünü kapsayıcıdır.
Örnek 1: Bir reklam şirketi bir diziyi izleyen kişi sayısının ne olacağı ve izleyenlerin
bazı özellikleri ile ilgili olabilir.
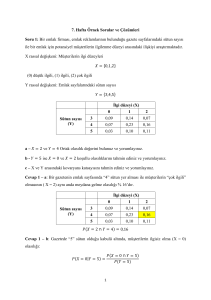
Yapılan alan araştırması sonucunda aşağıdaki sonuçlar elde edilmiştir.
İzlenme
Sıklığı
Düzenli
Ara Sıra
Hiç
Toplam
Gelir Düzeyi
Orta
0.13
0.11
0.17
0.41
Yüksek
0.04
0.10
0.13
0.27
Toplam
Düşük
0.04
0.06
0.22
0.32
0.21
0.27
0.52
1.00
A Olayları: İzleme Sıklığı
B Olayları: Gelir Düzeyi
A1 Olayı: Diziyi Düzenli İzleme
B1 Olayı: Yüksek Gelir Düzeyi
A2 Olayı: Diziyi Ara Sıra İzleme
B2 Olayı: Orta Gelir Düzeyi
A3 Olayı: Diziyi Hiç İzlememe
B3 Olayı: Düşük Gelir Düzeyi
Ai olayı üzerine odaklandığımızı kabul edelim.
,
ve
bağdaşmaz olaylardır. Ai olayının olasılığı, bu üç bağdaşmaz olayın olasılıklarının
birleşimidir.
( )
(
)
(
)
(
)
A2 Olayının olasılığı (Diziyi Ara Sıra İzleme) ile ilgili olduğumuzu düşünelim. Bu
durumda bu olayın gerçekleşme olasılığı (rassal olarak seçilen bir kişinin diziyi ara sıra izliyor
olma olasılığı), aşağıdaki gibi bulunabilir:
(
)
(
)
(
)
(
)
B3 Olayının olasılığı (Düşük Gelir Düzeyi) ile ilgili olduğumuzu düşünelim. Bu
durumda bu olayın gerçekleşme olasılığı (rassal olarak seçilen bir kişinin gelir düzeyinin
düşük çıkma olasılığı), aşağıdaki gibi bulunabilir:
(
)
(
)
(
)
(
)
Bulunan bu olasılıklara Kenar (Marjinal) Olasılıkları adı verilmektedir. A1, A2,…,Ai
olayları ile B1, B2,…,Bj olayları, ayrı ayrı olarak bağdaşmaz ve bütünü kapsayıcı
olduklarından kenar olasılıkları toplamı 1’e eşit olacaktır.
1
Çoğu zaman kenar olasılıklarından ziyade koşullu olasılıklar ile ilgiliyizdir. Örneğin
rassal olarak seçilen bir ailenin gelir düzeyinin yüksek olduğu bilindiğine göre, diziyi sürekli
izleme olasılığı nedir?
Koşullu Olasılık
(
( | )
(
(
)
(
)
|
( )
(
)
)
(
(
)
)
)
(
)
Rassal olarak seçilen bir ailenin gelir düzeyi düşükken diziyi ara sıra izleme olasılığı
nedir?
(
(
)
(
)
|
(
)
)
(
(
)
)
(
)
Diziyi hiç izlememe ile düşük gelir düzeyine sahip olma olayları istatistiksel olarak
birbirinden bağımsız mıdır?
İki olay, ancak ve ancak aşağıdaki koşulun sağlanması halinde istatistiksel olarak
bağımsızdır.
(
)
( ) ( )
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
Bu iki olay istatistiksel olarak bağımlıdırlar.
2
Örnek 2: Bir gazete okurlarına ekonomi sayfasını düzenli olarak okuyup
okumadıklarını ve aynı zamanda düzenli olarak hisse senedi alıp almadıklarını sormuştur.
Hisse Senedi Alımı
Ekonomi Sayfasını Okuma
Düzenli Ara Sıra
Hiç
0.18
0.10
0.04
0.16
0.31
0.21
Evet
Hayır
a – Rassal olarak seçilen bir okurun ekonomi sayfasını hiç okumama olasılığı nedir?
A Olayları: Hisse Senedi Alımı
B Olayları: Ekonomi Sayfasını Okuma
A1 Olayı: Evet, alırım.
B1 Olayı: Düzenli okurum.
A2Olayı: Hayır, almam.
B2 Olayı: Ara Sıra okurum.
B3 Olayı: Hiç okumam.
(
)
(
)
(
)
b – Rassal olarak seçilen bir okurun hisse senedi almış olma olasılığı nedir?
(
)
(
)
(
)
(
)
Gazete okurları arasından rassal olarak seçilen bir kişinin hisse senedi alıyor olma
olasılığı % 32’dir.
c–Ekonomi sayfasını hiç okumayan bir gazete okurunun hisse senedi alma olasılığı
nedir?
(
|
)
(
)
(
)
Ekonomi sayfasını hiç okumayan okurlar arasından rassal olarak seçilen bir kişinin
hisse senedi alıyor olma olasılığı % 16’dır.
d – Hisse senedi alan bir okurun ekonomi sayfasını hiç okumamış olma olasılığı
nedir?
(
|
)
(
)
(
)
Hisse senedi alan okurlar arasından rassal olarak seçilen bir kişinin gazetenin ekonomi
sayfasını hiç okumama olasılığı % 12.5’tir.
e – Hisse senedi almama ile ekonomi sayfasını hiç okumama olayları istatistiksel
olarak bağımsız mıdır?
3
İki olay, ancak ve ancak aşağıdaki koşulun sağlanması halinde istatistiksel olarak
bağımsızdır.
(
)
( ) ( )
(
(
)
(
)
(
)
(
(
)
)
)
(
(
)
)
Bu iki olay istatistiksel olarak bağımlıdırlar.
Konu tekrarı örnekleri: Bir kasabada yapılan IQ testi sonucunda, teste katılan
yetişkinlerin skorları çan eğrisi şeklinde dağılmakta, ortalama skor 100 ve standart sapmada
15 değerini almaktadır.
a – Teste katılan yetişkinlerin yüzde kaçının skoru 55 ve 145 aralığına düşmektedir?
Hatırlanacağı üzere çan eğrisi şeklinde bir dağılım söz konusu olduğunda, bir veri
setinde bulunan gözlem değerlerinin % 68’i, ortalamanın bir standart sapma sağında ve
solunda yer alır. Diğer bir ifadeyle, veri setinde yer alan yetişkinlerin % 68’inin IQ skorları 85
ve 115 aralığındadır.
Veri setinin çan eğrisi şeklinde dağıldığı varsayımı altında, veri setinde yer alan
gözlem değerlerinin % 95’i, ortalamaya 2 standart sapma mesafededir. Yani, veri setinde yer
alan yetişkinlerin % 95’inin IQ skorları 70 ve 130 aralığındadır.
Veri setinin çan eğrisi şeklinde dağıldığı varsayımı altında, veri setinde yer alan
gözlem değerlerinin % 99.7’si, ortalamaya 3 standart sapma mesafededir. Diğer bir ifadeyle,
veri setinde yer alan yetişkinlerin % 99.7’sinin IQ skorları 55 ve 145 aralığındadır.
4
RASSAL DEĞİŞKENLER
Bir rassal denemenin sonuçlarına göre belirlenen sayısal değerleri alan bir değişkendir.
Kesikli (Discrete) Rassal Değişkenler
Bir rassal değişken yalnızca sayılabilir değerler alabiliyorsa kesiklidir.
-
Bir saat içerisinde berbere gelen müşteri sayısı
-
Bir şirketin hesaplarında bulunan hata sayısı
Sürekli (Continuous) Rassal Değişkenler
Bir rassal değişken belirli bir aralıktaki bütün değerleri alabiliyorsa süreklidir.
-
Bir ailenin yıllık geliri
-
Türkiye’nin petrol ithalat miktarı
-
Yeni bir parçanın takılmasıyla bozulması arasında geçen süre
A – Kesikli Rassal Değişkenler ve Olasılık Dağılımları
A – 1 – Kesikli Rassal Değişkenlerin Beklenen Değeri
Kesikli bir rassal değişkenin beklenen değeri, şu şekilde tanımlanır:
( )
∑
(
)
(
)
(
)
(
)
Bir rassal değişkenin ortalamasına beklenen değer denir ve ( ) ile gösterilir.
Ancak buradaki ortalama kavramının ilk derslerde gördüğümüz merkezi eğilim
ölçülerinden olan aritmetik ortalamadan farklı olduğunun altını çizmek gerekmektedir.
Örnek (1): Bir yayınevi basmış olduğu kitaplardaki hata sayısı ile ilgilenmektedir.
Kitapların incelenmesi sonucunda kitap sayfalarının % 81’inde hiç hata olmadığı, % 17’sinde
“1” hata ve % 2’sinde de “2” hata olduğu tespit edilmiştir. Rassal olarak seçilmiş bir
sayfadaki hata sayısını X rassal değişkeni ile gösterirsek, bu rassal değişkenin alabileceği
değerlerin {
(
} olduğu görülür.
)
(
)
(
)
Bir sayfada oluşabilecek yanlış sayısının aritmetik ortalaması “1” olarak elde edilir.
Ancak bu değer, mevcut rassal değişkenin dağılımını tam olarak temsil etmemektedir. Zira
sayfaların % 81’inde hiç hata oluşmamış ve %2’sinde de 2 hata oluşmuştur. Rassal olarak
5
seçilen bir sayfada hata ile karşılaşma olasılığı, ortalama olarak, beklenen değer ile şu şekilde
hesaplanabilir:
( )
(
∑
)
( )(
)
( )(
)
( )(
)
Rassal olarak sayfalar sürekli incelendiğinde sayfa başına ortalama 0.21 hata bulmayı
bekleyebiliriz.
A – 2 – Kesikli Rassal Değişkenin Standart Sapması
Kesikli rassal bir değişkenin varyansı ve standart sapması da hesaplanabilir:
( )) ]
[(
(
(
∑
)
)
(
∑
(
)
( )
)
Kitap sayfalarındaki hata örneğimize geri dönecek olursak, aynı değerler için varyans ve
standart sapmayı hesaplayalım:
(
)
∑
(
)
(
( ) (
)
)
( )
( ) (
(
)
( ) (
)
)
Standart sapma, varyansın pozitif karekökü olacaktır:
√
A – 3 – Ortak Dağılımlı Kesikli Rassal Değişkenler
X ve Y kesikli iki rassal değişken olsun. Bunların Ortak Olasılık Fonksiyonu, X’in
belirli bir x değerini, Y’nin de belirli bir y değerini aynı anda olma olasılığını, x ve y’ni bir
fonksiyonu olarak gösterir.
(
)
(
)
Örnek (2): X rassal değişkeni tüketicilerin belirli bir şehirde yiyecek satan yerlerden
hoşnutluğunu, Y değişkeni de bu şehirde ikamet etme süresini temsil etsin. X rassal değişkeni,
düşük hoşnutluk düzeyinden yüksek hoşnutluk düzeyine doğru {
} değerlerini alsın. Y
rassal değişkeni de, şayet kişi bu şehirde 6 yıldan daha az süredir ikamet ediyorsa “1”, 6
yıldan daha uzun süredir ikamet ediyorsa “2” değerini alsın.
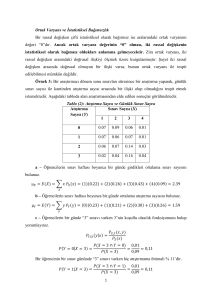
Tablo (1): İkamet Süresi ve Memnuniyet Düzeyi
İkamet
Memnuniyet Düzeyi (X)
Süresi (Y)
1
2
3
4
Toplam
0.04 0.14 0.23 0.07
0.48
1
0.07 0.17 0.23 0.05
0.52
2
0.11 0.31 0.46 0.12
1.00
Toplam
6
Rassal olarak seçilen bir tüketicinin bu şehirde 6 yıldan fazla süredir oturuyor olma ve
lokantalardan hiç memnun olmama olasılığı, aşağıdaki gibi ifade edilebilir:
(
)
(
)
Marjinal Olasılık Fonksiyonu
Rassal değişken X’in olasılık dağılım fonksiyonuna denir ve olanaklı bütün değerlerin
ortak olasılıklarının toplamı ile elde edilir:
( )
(
∑
)
Memnuniyetin “tam” (en yüksek) olma olasılığı, ikamet süresi değişkeni ile kesiştiği iki
değerin toplamı ile elde edilir:
(
)
(
∑
)
(
)
(
)
Rassal olarak seçilen bir kişinin bu şehirde 6 yıldan az süredir oturuyor olma olasılığı da
memnuniyet düzeyi değişkeninin bütün kesişim değerlerinin toplamı ile bulunur:
(
)
(
∑
)
(
)
(
)
(
)
(
)
Koşullu Olasılık Fonksiyonları
X rassal değişkeni için x değeri belirlenmişken, Y rassal değişkeninin y değerini alma
olasılığını y değerinin bir fonksiyonu olarak ifade eder.
|
( | )
(
)
( )
|
( | )
(
)
( )
Tablo (1)’deki verilerden hareketle tüketici hoşnutluğu “2” değerini almışken oturma
süresinin “1” değerini alma olasılığı, aşağıdaki gibi hesaplanabilir:
|
( | )
(
|
(
)
( )
)
(
)
(
)
Tüketicinin oturma süresinin 6 yıldan fazla olduğu bilindiğine göre, hoşnutluk
düzeyinin “4” değerini alma olasılığı nedir?
(
|
)
(
)
( )
(
)
(
)
Bağımsızlık
X ve Y rassal değişkenlerin ortak olasılık fonksiyonları, ancak ve ancak, marjinal
olasılık fonksiyonlarının çarpımına eşitse X ve Y rassal değişkenleri bağımsızdır denir.
(
)
( )
7
( )
A – 4 – Ortak Varyans (Covariance)
X ve Y rassal değişkenlerinin istatistiksel olarak bağımlı iki rassal değişken olduğunu
düşünelim. Bu iki değişken arasındaki ilişkinin gücü ve özellikleri bizim için önemlidir.
Farklı iki rassal değişken arasındaki ilişkiler çok farklı formlarda olabilir (kübik, conveks,
konkav, parabol vs…). Bu durumda basitlik adına, iki rassal değişken arasındaki doğrusal
ilişki ile ilgilenelim. Örneğin X’in düşük bir değeri, ortalama olarak, Y’nin düşük bir değerine;
X’in yüksek bir değeri, Y’nin yüksek bir değerine öyle bir denk gelebilir ki bir serpilme
diyagramı çizilse aralarında bir doğru çizilebilir. Rassal değişken X’in ortalaması
olsun. (
değişken Y’nin ortalaması
ve rassal
) çarpımını ele alalım. Şayet X’in düşük
X)(
değerleri Y’nin düşük değerlerine; X’in yüksek değerleri, Y’nin yüksek değerlerine karşılık
geliyorsa bu çarpım işleminin değerinin pozitif olması beklenir. Tersine X’in düşük değerleri
Y’nin yüksek değerlerine; X’in yüksek değerleri, Y’nin düşük değerlerine karşılık geliyorsa,
bu çarpımın beklenen değeri negatif olur. (
) çarpımının beklenen değeri “0”
X)(
oluyorsa, X ve Y rassal değişkenleri arasında doğrusal bir ilişki yoktur yorumunu yapabiliriz.
Demek ki anakütledeki doğrusal ilişkinin bir ölçüsü olarak (
) çarpımının
X)(
beklenen değerini incelemeliyiz.
(
)
( ))(
(
(
)
( )]
(
∑∑
)
( ) ( )
( ) ( )
Örnek bir uygulama olarak tüketici memnuniyeti ile ikamet süresi arasındaki ortak
varyansı tablo (1)’deki verilerden hareketle hesaplayalım. Öncelikle iki rassal değişkenin
beklenen değerini (ortalamalarını) hesaplayalım:
( )
∑
( )(
∑
∑∑
(
(
)
(
)
( )(
)
( )(
)
( )
( )(
)
( )(
)
( )(
)
)
( )( )(
)
( )( )(
)
( )( )(
)
( )( )(
)
( )( )(
)
( )( )(
)
( )( )(
)
( )( )(
)
)
(
)
( ) ( )
(
)(
)
Ortak varyansın negatif bir değer almasının anlamı, bu şehirde ikamet süresi arttıkça
lokantalardan memnuniyet düzeyinin düşmesidir.
8