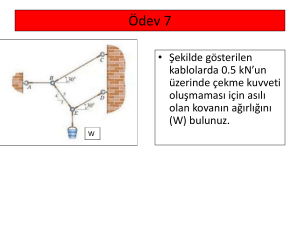
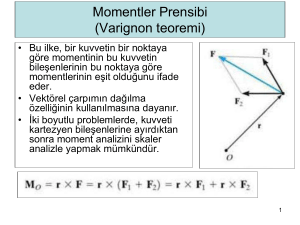
EĞİLME (Kesme ve Moment Diyagramları)

EĞİLME
Köprünün tabyası onun eğilme gerilmesine karşı
koyma dayanımı esas alınarak boyutlandırılır.
EĞİLME
Mühendislikte en önemli yapı ve makine elemanları mil ve kirişlerdir. Bu
bölümde, mil ve kirişlerde eğilmenin sebep olduğu gerilme belirlenecektir.
Öncelikle, kiriş veya mil için kesme ve moment diyagramının nasıl
oluşturulacağı ele alacağız. Normal kuvvet ve tork diyagramları gibi kesme ve
moment diyagramları da elemandaki hem en büyük kesme ve momentin
büyüklüğünü hem de yerinin belirlenmesi için oldukça kullanışlı grafikler sağlar.
Bir kesitteki iç momentin belirlenmesinden sonra eğilme gerilmesi
hesaplanabilir. Öncelikle, simetrik kesitli lineer elastik homojen malzemeden
doğrusal elemanlar ele alınacaktır.
Basit mesnetli kiriş
Konsol kiriş
Basit mesnetli çıkmalı kiriş
EĞİLME
İnce ve boyuna eksenine dik doğrultuda uygulanan yükleri taşıyan yapı
elemanları kiriş olarak adlandırılır. Kirişler, genellikle sabit kesitli doğrusal ve
uzun çubuklar olup çoğu kez mesnet şekillerine göre sınıflandırılırlar. Örneğin,
Şekil görüldüğü üzere basit mesnetli kiriş bir ucundan pim (mafsal) diğer
ucundan kayar mesnetli, konsol kiriş bir ucu sabit diğer ucu serbest ve çıkmalı
kiriş bir ucu pim bağlı diğer ucu veya uçları ise kayıcı mesnet üzerine serbestçe
uzanır. Bütün yapı elemanları arasında en önemlisinin kiriş olduğu söylenir.
Binanın döşemesinde, köprünün tabyasında veya uçak kanadının taşınmasında
kirişler kullanılır. Ayrıca, otomobilin aksı, vincin kolu, vücudumuzdaki
kemiklerin birçoğu kiriş olarak görev yaparlar.
Basit mesnetli kiriş
Konsol kiriş
Basit mesnetli çıkmalı kiriş
EĞİLME (Kesme ve Moment Diyagramları)
Uygulanan yükler sebebiyle kirişlerde genellikle kiriş ekseni boyunca bir
noktadan diğerine değişen iç kesme kuvveti ve eğilme momenti meydana
gelir. Bu yüzden uygun bir kiriş tasarımı için öncelikle kirişteki maksimum
kesme ve eğilme momentinin belirlenmesi gerekir. Bunların elde edilmesinin
bir yöntemi de V (kesme) ve M (moment) nin kiriş ekseni boyunca herhangi
bir x mesafenin fonksiyonu olarak ifade edilmesidir. Elde edilen bu kesme ve
moment fonksiyonlarının grafiği çizilerek diyagram olarak sunulur. Bu
grafiklere kesme ve moment diyagramları denir. V ve M’ nin maksimum
değerleri bu grafiklerden kolayca elde edilir. Ayrıca, bu diyagramlardan
kiriş ekseni boyunca kesme kuvveti ve eğilme momentindeki değişimler
hakkında detaylı bilgi sağladığı için genellikle mühendisler tarafından
kirişin takviye edilmesi gereken yerlerini veya kiriş uzunluğu boyunca farklı
noktalarda kiriş boyutunun nasıl değiştiğini belirlemek için kullanılırlar.
V ve M’ yi x terimiyle formüle etmek için x pozisyonun orijin ve pozitif
yönünün seçimi yapılmalıdır. Seçim keyfi olmakla birlikte, çoğu zaman
orijin kirişin sol ucuna yerleştirilir ve pozitif yön sağa doğru kabul edilir.
EĞİLME (Kesme ve Moment Diyagramları)
Genellikle, x’ e bağlı elde edilen iç kesme ve moment fonksiyonları, yayılı
kuvvetlerinin değişim gösterdiği noktalar ile tekil kuvvet ve momentin
uygulandığı noktalarda süreksiz olacak veya eğimleri süreksiz olacaktır. Bu
yüzden kesme ve moment fonksiyonları kirişteki yüklemenin süreksiz
olduğu iki noktası arasındaki her bir bölge için belirlenir. Örneğin, şekildeki
kiriş uzunluğu boyunca V kesme ve M momentinin değişimini ifade ederken
x1, x2 ve x3 koordinatları kullanılacaktır. Bu koordinatlardan x1 sadece A dan
B ye, x2 B den C ye ve x3 C den D ye kadar olan bölgede geçerlidir.
EĞİLME (Kesme ve Moment Diyagramları)
Kiriş İçin İşaret Kabulü. İşaret kabulünün seçimi keyfi olsa da, biz burada
mühendislik uygulamalarında yaygın olarak tercih edilen ve şekilde görülen
işaret kabulünü kullanacağız. Pozitif yönler şu şekildedir: Yayılı yük, kirişe
yukarı doğru etki eder. İç kesme kuvveti, etki ettiği kiriş parçasının saat
yönünde dönmesine sebep olur. İç moment, kiriş parçasının üst liflerinde
kısalma meydana getirecektir. Böyle eğilen bir kiriş, içinde ‘akışkan
tutabilecek’ şekildedir. Bunlara zıt yönde olan yüklemeler negatif olacaktır.
Pozitif dış yayılı yük
Pozitif iç kesme yükü
Pozitif iç moment
Pozitif İşaret Kabulü
EĞİLME (Kesme ve Moment Diyagramları)
ÖRNEK: Şekilde görülen üniform yayılı yüke maruz basit mesnetli kirişin kesme
ve moment diyagramını çiziniz.
ÇÖZÜM
Mesnet Tepkileri. Mesnet tepkileri hesaplanır.
Kesme ve Moment Fonksiyonları. Kirişin sol parçasının serbest cisim diyagramı
Şekil b de görülmektedir. Bu parça üzerindeki yayılı yükün bileşkesi olan wx
kuvveti sadece serbest cisim diyagramının izole edilmesinde gösterilir. Bu kuvvet,
yayılı yük içeren alanın ağırlık merkezinden ya da kirişin sağ ucundan x/2
mesafeden etki eder. İki denge denkleminin uygulanarak iç kuvvetler elde edilir.
≤ ≤ Aralığında
+↑ ∑
= ;
↶+ ∑
= ;
−
−
+
−
=
+
=
=
( − )
(1)
=
−
(2)
EĞİLME (Kesme ve Moment Diyagramları)
=
=
( − ) Kesme Fonksiyonu
−
Moment Fonksiyonu
Kesme ve Moment Diyagramları.
Kesmenin sıfır olduğu nokta Denklem (1)
den bulunur.
=
2
−
=
2
=0
EĞİLME (Kesme ve Moment Diyagramları)
ÖRNEK: Şekilde görülen kirişin kesme ve moment diyagramını çiziniz.
ÇÖZÜM
Mesnet Tepkileri. Mesnet tepkileri hesaplanır.
Kesme ve Moment Fonksiyonları. Kirişin ortasında hem tekil kuvvet hem de yayılı
yük süreksizliği olduğu için kirişin tamamı için kesme ve moment fonksiyonları
ifade edilirken iki sürekli bölge için x tanımlanır.
EĞİLME (Kesme ve Moment Diyagramları)
≤
≤
(AB aralığı sürekli bölge)
+↑ ∑
.
= ;
− =
↶+ ∑
−
= ;
− .
= .
+
=
=
(1)
.
+
(2)
EĞİLME (Kesme ve Moment Diyagramları)
≤
≤
+↑ ∑
.
= ;
−
↶+ ∑
−
= ;
− .
(BC aralığı sürekli bölge)
−
⁄
+
= − .
−
−
−
+
=
=
⁄
+
.
+
.
.
−
−
(3)
+
(4)
=
EĞİLME (Kesme ve Moment Diyagramları)
≤
≤
(AB aralığı sürekli bölge)
= .
=
(1)
.
+
≤
≤
=
.
= − .
(2)
(BC aralığı sürekli bölge)
−
(3)
+
.
+
.
(4)
NOT: Bu sonuçlar, dV/dx=w ve V=dM/dx den
her bir parça için kontrol edilebilir. Ayrıca
x1=0 iken Denklem (1) ve (2) den V=5.75 kN ve
M=80 kNm elde edilir; x2=10 m iken Denklem
(3) ve (4) den V= –34.25 kN ve M=0 elde edilir.
Bu değerler, serbest cisim diyagramı üzerinde
görülen mesnet tepkileri ile kontrol edilebilir.
EĞİLME (Kesme ve Moment Diyagramları)
Kesme ve Moment Diyagramı Oluşturulmasında Grafik Yöntem: Kirişin birkaç
farklı yüklemeye maruz kaldığı durumda, V kesme ve M moment fonksiyonunun
x uzunluğa bağlı olarak ifade edilip daha sonra bu denklemlerin grafiklerinin
çizilmesi oldukça uzun hatta sıkıcı olabilmektedir. Bu bölümde, kesme ve
moment diyagramını oluşturmak için biri yayılı yük ile kesme kuvveti ve diğeri
kesme kuvveti ile moment arasındaki ilişkiyi, iki diferansiyel bağıntıya
dayandıran basit ve pratik bir yöntem ele alınacaktır.
EĞİLME (Kesme ve Moment Diyagramları)
Yayılı Yük Bölgeleri. Genelleştirme yapmak amacıyla gelişi güzel yüklemeye
maruz Şekil a da görülen kirişi göz önüne alalım. Kirişin x uzunluğundaki çok
küçük parçasının serbest cisim diyagramı Şekil b de görülmektedir. Tekil kuvvet ve
momentin olmadığı x mesafesinde seçilen bu parça için elde edilecek sonuçlar tekil
yük noktaları için uygulanmayacaktır.
x parçasının serbest cisim
diyagramı
EĞİLME (Kesme ve Moment Diyagramları)
Şerit elemana etki eden bütün yüklerin pozitif yönlerde oluşturulduğuna dikkat ediniz.
Bununla birlikte, şerit elemanı dengede tutmak için parçanın sağ yüzüne etki eden hem
bileşke iç kesme hem de moment küçük miktarda değişmelidir. ∆x üzerinde yaklaşık sabit
kabul edilen yayılı yük, sağ yüzeyden 1/2 x mesafeden etki eden w(x)x bileşke kuvvetle
değiştirilebilir. Şerit elemana denge denklemleri uygulanarak kesme ve momentteki
değişim elde edilir.
+↑ ∑
= 0;
−
∆ −
+∆
∆ =−
=0
∆
∆
=− ( )
∆
Kesme diyagramında bir noktanın eğimi = − bir noktadaki yayılı yükün büyüklüğü
+↺ ∑
= 0;
− ∆ −
+
∆
∆
= ∆ −
∆
+
+∆
=0
∆
∆
= ( )
∆
Moment diyagramında bir noktanın eğimi = Bir noktadaki kesme kuvvetinin büyüklüğü
x parçasının serbest
Cisim diyagramı
EĞİLME (Kesme ve Moment Diyagramları)
Tekil Kuvvet ve Moment Bölgesi. Şekilde tekil kuvvetin etki ettiği kiriş
üzerindeki bir noktadan alınan küçük dilim elemanın serbest cisim diyagramı
şekil (a) da gösterilmiştir. Dengede olan bir kiriş üzerinden alınan elemanın da
dengede olması gerektiği için denge denklemleri sağlanmalıdır.
+↑ ∑
= ;
−
−
+∆
=
∆ =−
Kiriş üzerine F kuvvetinin aşağı doğru etki etmesi halinde, ∆
negatif
olacağından kesme kuvveti aşağı yönde sıçrama yapar. Aynı şekilde, F kuvveti
yukarı doğru etki ederse, sıçrama ∆ yukarı doğru olacaktır.
EĞİLME (Kesme ve Moment Diyagramları)
Benzer olarak, Şekil (b) den moment dengesi yazılarak momentteki değişim
belirlenebilir.
+↺ ∑
∆ →
= ;
+∆
olması halinde,
−
−
∆
∆ −
=
=
Bu durumda, eğer
saat ibreleri dönme yönünde uygulanmaktaysa, ∆ pozitif
olacağından moment diyagramı yukarı doğru sıçrama yapar. Aynı şekilde,
saat
ibreleri tersi dönme yönündeyse sıçrama ∆ aşağı doğru olacaktır.
EĞİLME (Kesme ve Moment Diyagramları)
ÖRNEK: Şekilde görülen kirişin kesme kuvveti ve eğilme momenti diyagramını
çiziniz.
ÇÖZÜM:
Mesnet Tepkileri. Basit mesnetli kirişin hesaplanan reaksiyon kuvvetleri şekil (b)
deki serbest cisim diyagramında gösterilmektedir.
EĞİLME (Kesme ve Moment Diyagramları)
Kesme Kuvveti Diyagramı. Başlangıç noktasında, .
kuvvet yukarı doğru etki
etmekte olduğundan
=+ .
dur. ve arasında yayılı yük etki etmediğinden
⁄
= kesme kuvveti sabit kalır.
noktasında,
aşağı doğru olduğundan
kesme kuvveti, + ,
dan − .
’ na aşağı doğru
luk sıçrama yapar. Bu
noktada yine
den ye kesme kuvveti sabit kalır. Kesme kuvveti de, aşağı doğru
bir sıçrama daha yaparak − .
değerine erişir. Sonunda, ve
arasında
yayılı yük olmadığından − .
da sona erişir.
EĞİLME (Kesme ve Moment Diyagramları)
Moment Diyagramı. Kirişin her ucundaki
moment sıfırdır.
Moment diyagramında, dan ye eğim + .
sabittir.
deki momentin değeri,
ile
arasında kesme diyagramının altında kalan
alandan belirlenir. ∆
= .
=
.
dir.
=
olduğundan
=
+∆
veya + .
= .
dir.
Moment diyagramındaki eğim, noktasından
noktasına erişene kadar − . dir.
Momentin büyüklüğü,
den
ye kesme
kuvveti diyagramında altında kalan alandan
bulunur. ∆
=− .
=− .
ve
= .
− .
= .
dir. Bu şekilde devam ederek
deki değere
erişilir ve diyagram kapanır.
EĞİLME (Doğrusal Elemanın Eğilme Deformasyonu)
Bu bölümde, homojen malzemeden doğrusal prizmatik
bir kirişin eğilmeye maruz kalması halinde oluşan
deformasyonlar incelenecektir. Bu inceleme, şekilde
görüldüğü gibi, kesiti bir eksenine göre simetriye sahip ve
eğilme momenti de simetri eksenine dik ( ) ekseni
etrafında etki etmekte olan kirişlerle sınırlı olacaktır.
Kauçuk gibi yüksek deformasyon kabiliyetine sahip malzeme kullanarak düzgün
prizmatik bir elemanın eğilme momentine maruz kalması durumunda, fiziksel olarak
neler olacağı görülebilir.
EĞİLME (Doğrusal Elemanın Eğilme Deformasyonu)
Örneğin, Şekil (a) da enine ve boyuna çizgilerle işaretli kare kesitli deforme olmamış
çubuğu göz önüne alalım. Eğilme momenti uygulandığında, çubuğun üzerindeki bu
çizgiler Şekil (b) de görüldüğü gibi çarpılır. Boyuna çizgiler, eğriye dönüşürken dikey
enine çizgiler, doğrusal kalmakla birlikte dönmeye maruz kalır.
Eğilme momenti çubuğun alt kısmında gerginliğe sebep olurken üst kısmındaki baskıya
sebep olur. Bunun sonucunda, bu iki bölge arasında malzemenin boyuna liflerinin
uzunluklarının değişime maruz kalmadığı tarafsız yüzey denilen nötr bir yüzey olmalıdır.
Yatay çizgiler eğri olur
Dikey çizgiler doğrusal kalmakla birlikte döner
Deformasyondan önce
Deformasyondan sonra
EĞİLME (Doğrusal Elemanın Eğilme Deformasyonu)
Bu gözlemlerden, cismin deformasyonu ile ilgili üç varsayımı yapabiliriz.
Birincisi, tarafsız yüzey boyunca uzanan x ekseninin uzunluğu her hangi bir
değişikliğe uğramaz. Moment, kirişi deforme etme meylinde olduğundan bu çizgi,
x–y simetri düzleminde uzanan bir eğri olur. İkincisi, kirişin bütün kesitleri düzlem
kalırken boyuna eksene de diktirler. Üçüncüsü, kesitin kendi düzlemi içindeki
deformasyon ihmal edilecektir. Kesit düzleminde uzanan ve kesitin etrafında
döndüğü z ekseni, tarafsız eksen olarak adlandırılır.
Tarafsız
eksen
Boyuna
eksen
Tarafsız
yüzey
EĞİLME (Doğrusal Elemanın Eğilme Deformasyonu)
Bu eğilme etkisinin cisimde nasıl bir şekil değişimi meydana getirdiğini göstermek için
kiriş uzunluğu boyunca her hangi bir x mesafedeki x kalınlığa sahip deforme olmamış
kiriş parçasını izole edeceğiz. Kirişten alınan bu elemanın deforme olmamış ve deforme
olmuş durumlarının yan görünüşleri Şekilde görülmektedir.
Deformasyondan önce
Deformasyondan sonra
EĞİLME (Doğrusal Elemanın Eğilme Deformasyonu)
=
=
Bu zorlanmayı, elemanın y konumu ve boyuna
ekseninin eğrilik yarıçapı ρ cinsinden ifade
edelim. Deformasyondan önce, ∆s=∆x dir.
Deformasyondan sonra, ∆x uzunluğunun eğrilik
merkezi O' ve eğrilik yarıçapı ρ olur. Elemanın
kenarları arasındaki açı ∆θ olarak tanımlandığı
için ∆x=∆s=ρ ∆θ dır. Benzer şekilde, ∆s in
deforme olmuş uzunluğu s=(ρ–y)∆θ olur. Bu
değerler, yukardaki denklemde yerine yazılırsa
=
∆
∆
∆ →
−
∆ →
=−
∆
∆
∆ − ∆
∆
EĞİLME (Doğrusal Elemanın Eğilme Deformasyonu)
=−
Bu önemli sonuç, kiriş üzerindeki herhangi bir elemanın boyuna zorlanma
değerinin kesit üzerindeki bir noktanın y konumuna ve boyuna ekseninin eğrilik
yarıçapına bağlı olduğunu gösterir. Bir başka ifadeyle, belirli bir kesit için
boyuna normal zorlanma tarafsız eksenden uzaklık olan y mesafesi ile
lineer değişecektir. Tarafsız eksenin (+y) kadar üzerindeki liflerde kısalma
(–ϵ) zorlanma oluşurken (–y) kadar altındaki liflerde uzama (+ϵ) oluşur.
Zorlanmadaki bu değişim kesit üzerinde görülmektedir. Burada, en büyük
zorlanma tarafsız eksenden y=c mesafede bulunan en dıştaki liflerde
oluşur. ϵmaks=ρ⁄c olduğu için hangi bir noktadaki zorlanma
=−
⁄
⁄
veya
=−
EĞİLME (Doğrusal Elemanın Eğilme Deformasyonu)
Bu normal zorlanma, sadece deformasyonla ilgili kabuller esas alınarak
belirlenmiştir. Kirişe moment uygulandığında sadece boyuna doğrultuda normal
gerilme meydana getirecektir. Diğer bütün normal ve kayma gerilme bileşenleri
sıfır olacaktır. Tek eksenli gerilmeyi ifade eden bu durum ϵx zorlanma bileşeni
oluşmasına sebep olur. Ayrıca, bu deformasyonları burada ihmal etmemize
rağmen, Poisson oranı ile kesit alan düzlemini deforme eden ϵy=–vϵx ve ϵz=–vϵx
zorlanma bileşenleri arasında da ilişki olmalıdır. Bununla birlikte, bunun gibi
deformasyonlar kesitin tarafsız ekseninin alt kısmındaki boyutlarda küçülmeye
sebep olurken tarafsız ekseninin üst kısmındaki boyutlarında büyümeye sebep
olur. Örneğin, kiriş kare kesitli ise, aslında Şekilde görüldüğü gibi deforme
olacaktır.
EĞİLME (Eğilme Formülü)
Şimdi, kiriş kesitine etki eden bileşke iç eğilme momentini kirişteki gerilme
dağılımıyla ilişkilendiren denklemi elde edeceğiz. Bunu yapmak için malzemenin
lineer elastik davrandığını varsayacağız. Şekil (a) da görülen normal zorlanma
değişiminin lineer olması Şekil (b) de de görülen normal gerilme değişiminin de
lineer olması sonucunu doğurur. Bu yüzden, normal zorlanmanın değişimine
benzer olarak σ normal gerilme de elemanın tarafsız ekseninde sıfırdan en uzak
mesafe c ye lineer olarak değişerek maksimum değerini σmaks alır.
Şekil (a). Normal zorlanma değişimi
Şekil (b). Normal gerilme değişimi
EĞİLME (Eğilme Formülü)
Benzer üçgenler veya Hook kanunu σ=Eϵ kullanarak normal gerilme,
=−
Bu denklem, kesitteki gerilme dağılımını tarif eder. Pozitif M momenti +z
yönünde, y nin pozitif değerleri için σ normal gerilme negatif olup negatif x
yönünde etki ettiği için basınç gerilmesidir. Kesitin belirli bir noktasından seçilen
hacim elemana sadece çekme veya basınç gerilmesi etki edecektir. Örneğin, +y
pozisyonundaki bir elemanın gerilme durumu, Şekilde görülmektedir.
EĞİLME (Eğilme Formülü)
Tarafsız eksenin yerini, kesite etki eden gerilme
dağılımının meydana getirdiği bileşke kuvvetin
sıfıra eşit olması gereğini ifade eden uygunluk
şartından buluruz. Şekilde keyfi seçilmiş dA
elemanına etki eden kuvvet dF= σdA olarak
yazarız.
=∑
= ;
=
=
=
=
−
−
⁄ sıfıra eşit olamayacağı için
−
integralin sıfıra eşit olması gerekir.
=
Eleman kesit alanının tarafsız eksen etrafındaki birinci momenti sıfır olmalıdır. Bu şart,
sadece tarafsız eksenin aynı zamanda kesitin yatay ağırlık merkezi ekseni olmasıyla
sağlanabilir. Yani, Kesitinin ağırlık merkezi belirlendiğinde tarafsız eksenin yeri de bilinir.
EĞİLME (Eğilme Formülü)
Kirişteki gerilme, gerilme dağılımının tarafsız eksen etrafında meydana getirdiği
momentin bileşke iç momente eşit olması gereğinden belirlenir. dF nin Şekildeki tarafsız
eksen etrafındaki momenti dM=y dF dir. dF=σ dA olduğundan = −
ifadesi
kullanılarak bütün kesit için moment yazılır.
=∑
;
=
=
=
=
Eşitlikteki integral, kesit alanın tarafsız ekseni etrafındaki atalet momentini temsil eder.
Bunu I ile sembolize edeceğiz. Moment ifadesinden σmaks çekilerek aşağıdaki formda
yazılır.
=
EĞİLME (Eğilme Formülü)
=
Burada
σmaks = elemanın kesiti üzerinde tarafsız eksene en uzak noktada oluşan
maksimum normal gerilme
M = kesim metodu ve denge denklemlerinden belirlenen kesitin tarafsız
ekseni etrafında hesaplanan bileşke iç moment
c = tarafsız eksenden en uzak noktaya olan dik mesafe. Bu nokta, σmaks etki
ettiği yerdir.
I = kesit alanın tarafsız ekseni etrafında hesaplanmış atalet momenti
EĞİLME (Eğilme Formülü)
⁄ = − ⁄ olduğu için her hangi bir y mesafesindeki normal gerilme benzer
σ
formülle belirlenir.
=−
Negatif işaret, oluşturulan x, y, z eksenleriyle işaret uyumu için gereklidir. Sağ el
kuralına göre, hem +z ekseni etrafındaki M hem de yukarı doğru y pozitiftir. Bu
durumda, σ negatif x yönünde etki edeceği için negatif (basınç) olmalıdır.
Yukarıdaki denklemler eğilme formülü olarak anılır. Kesiti bir eksenine göre
simetriye sahip ve momentin de bu eksene dik olarak etki ettiği doğrusal
elemanlarda normal gerilmenin hesaplanması için kullanılır.