Ders Kodu, Adı
T+U/K
Yıl / Yarıyıl
Düzey
Yazılım Şekli
Bölüm
Ön Koşul
Öğretim Yöntemi
Süresi (Hafta-Saat)
Öğretim Dili
Dersin Amacı
Dersin İçeriği
Değerlendirme
Sistemi
AKTS İş Yükü
Tablosu
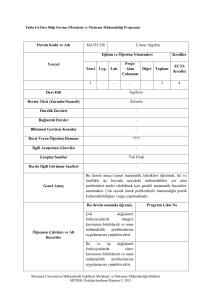
DERS BİLGİ FORMU
MAT 118 MATEMATİK-2
4+0/4
AKTS Kredisi
5
1. Yıl / Güz Dönemi
Lisans
Zorunlu
Gıda Mühendisliği
Yok
Anlatım-sunum
14 hafta-haftada 4 saat teorik
Türkçe
Öğrencilere temel matematik tekniklerini öğretmek, problemleri analiz edebilmek
için gerekli matematik becerileri tanıtmak ve çok sayıda örnek problemlerle
matematiğin pratik kullanımına vurgu yapmaktır.
Matrisler, determinantlar, özdeğerler ve özvektörler, ters matris. Lineer denklem
sistemleri ve eşelon form yardımı ile çözüm ve Crammer yöntemi. Konik kesitleri ve
kuadratik denklemler, kutupsal koordinatlar ve grafik çizimleri, düzlemdeki eğrilerin
parametrizasyonu. Üç boyutlu uzay ve kartezyen koordinatlar. düzlemde ve uzayda
vektörler. Nokta, vektörel ve karma çarpımlar. Üç boyutlu uzayda doğrular ve
düzlemler. Silindirler, koniler ve küre. Silindirik ve küresel koordinatlar. Vektör
değerli fonksiyonlar ve uzayda eğriler, eğrilik, burulma ve TNB çatısı. Çok
değişkenli fonksiyonlar, limit. süreklilik ve kısmi türevler. Zincir kuralı, doğrultu
türevleri, Gradyan, Diverjans, Rotasyonel, ve teğet düzlemler. Ekstrem değerler ve
eyer noktaları, Lagrange çarpanları, Taylor ve Maclaurin serileri. İki katlı integraller,
alan, moment ve ağırlık merkezi. Kutupsal formda iki katlı integraller. Kartezyen
koordinatlarda üç katlı integraller. Üç boyutlu uzayda kütle, moment ve ağırlık
merkezi. Silindirik ve küresel koordinatlarda üç katlı integraller. Çok katlı
integrallerde değişken dönüşümü. Eğrisel integraller, vektör alanları, iş, akı.
Düzlemde Green Teoremi. Yüzey alanı ve yüzey integralleri. Stokes Teoremi,
Diverjans Teoremi ve uygulamaları.
Yarıyıl İçi Çalışmalar
Sayısı
Katkı %
Ara Sınav
1
40
Kısa Sınav
Ödev
Devam
Uygulama
Toplam
1
Yarıyıl İçi Çalışmaların Başarıya Katkısı
40
Yarıyıl Sonu Sınavının Başarıya Katkısı
60
Toplam
100
Etkinlik
Sayısı
Süresi (saat) Toplam İş Yükü (saat)
Ders Süresi
14
4
56
Sınıf Dışı Ders
14
6
84
Çalışma Süresi
Ödevler
Sunum / Seminer
Hazırlama
Ara Sınavlar
1
1
1
Öğrenim Çıktıları
Proje
Yarıyıl Sonu Sınavı
1
2
2
Dersi başarıyla tamamlayan öğrenci;
Toplam İş Yükü (saat)
143
1.Matris ve determinant kavramlarını tanıyıp denklem sistemlerini çözebilir.
Dersin
AKTS
Kredisi
5
2.Konik kesitlerini tanıyarak, kutupsal koordinatlarda ifade edebilir.
3.İki ve üç boyutlu uzayda vektörleri bilir.
4.Çok değişkenli fonksiyon ve özelliklerini kavrar.
5.Çok değişkenli fonksiyonlarda limit ve süreklilik kavramını bilir.
6.Çok değişkenli fonksiyonlarda türev kavramını bilebilir, mühendislik
problemlerine uygulamasını yapar.
7.Çok değişkenli fonksiyonlarda integral kavramını bilebilir, mühendislik
problemlerine uygulamasını yapar.
8.Yüzey integralini mühendislik problemlerine uygular.
Ders Akışı
Hafta
No
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Ön
Hazırlıklar
Matrisler, Determinantlar, Özdeğerler ve Sunum
Özvektörler, Ters Matris
Hazırlama
Lineer Denklem Sistemleri ve Eşelon Form Sunum
Yardımı ile Çözüm ve Crammer Yöntemi.
Hazırlama
Konik Kesitleri ve Kuadratik Denklemler, Sunum
Kutupsal Koordinatlar ve Grafik Çizimleri, Hazırlama
Düzlemdeki Eğrilerin Parametrizasyonu
Üç Boyutlu Uzay ve Kartezyen Koordinatlar, Sunum
Düzlemde ve Uzayda Vektörler, Nokta, Hazırlama
Vektörel ve Karma Çarpımlar
Üç Boyutlu Uzayda Doğrular ve Düzlemler, Sunum
Silindirler, Koniler ve Küre, Silindirik ve Hazırlama
Küresel Koordinatlar
Vektör Değerli Fonksiyonlar ve Uzayda Sunum
Eğriler, Eğrilik, Burulma ve TNB Çatısı.
Hazırlama
Çok Değişkenli Fonksiyonlar, Limit, Sunum
Süreklilik ve Kısmi Türevler
Hazırlama
Ara Sınav
Zincir Kuralı, Doğrultu Türevleri, Gradyan, Sunum
Diverjans, Rotasyonel, ve Teğet Düzlemler Hazırlama
Ekstrem Değerler ve Eyer Noktaları, Sunum
Lagrange Çarpanları, Taylor ve Maclaurin Hazırlama
Serileri
İki Katlı İntegraller, Alan, Moment ve Sunum
Ağırlık Merkezi, Kutupsal Formda İki Katlı Hazırlama
İntegraller, Kartezyen Koordinatlarda Üç
Katlı İntegraller
Üç Boyutlu Uzayda Kütle, Moment ve Sunum
Ağırlık Merkezi, Silindirik ve Küresel Hazırlama
Koordinatlarda Üç Katlı İntegraller, Çok
Katlı İntegrallerde Değişken Dönüşümü.
Konular
Dokümanlar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
13.
14.
15.
Dersin Kaynakları
Dersin Bölüm
Öğrenim
Çıktılarına Katkısı
Dersin Yetkilileri
Eğrisel İntegraller, Vektör Alanları, İş, Akı, Sunum
Düzlemde Green Teoremi.
Hazırlama
Yüzey Alanı ve Yüzey İntegralleri, Stokes Sunum
Teoremi,
Diverjans
Teoremi
ve Hazırlama
Uygulamaları
Stokes Teoremi, Diverjans Teoremi ve Sunum
Uygulamaları.
Hazırlama
Önerilen
Kaynaklar
Önerilen
Kaynaklar
Önerilen
Kaynaklar
1.Thomas, G.B. ve Finney, R.L.,Çev: Korkmaz, R., 2001; Calculus ve Analitik
Geometri, Cilt II, Beta Yayınları, İstanbul.
2.Balcı, M. 2009; Genel Matematik 2, Balcı Yayınları, Ankara.
3.Kolman, B. ve Hill, D.L., Çev Edit: Akın, Ö. 2002 ; Uygulamalı Lineer Cebir,
Palme Yayıncılık, Ankara.
Dersin Öğrenim Çıktıları
Bölüm Öğrenim
Çıktıları
1.Matris ve determinant kavramlarını tanıyıp denklem
1
sistemlerini çözebilir.
2.Konik kesitlerini tanıyarak, kutupsal koordinatlarda ifade
1, 2
edebilir.
3.İki ve üç boyutlu uzayda vektörleri bilir.
1
4.Çok değişkenli fonksiyon ve özelliklerini kavrar.
1
5.Çok değişkenli fonksiyonlarda limit ve süreklilik kavramını
1
bilir.
6.Çok değişkenli fonksiyonlarda türev kavramını bilebilir,
1, 3
mühendislik problemlerine uygulamasını yapar.
7.Çok değişkenli fonksiyonlarda integral kavramını bilebilir,
1
mühendislik problemlerine uygulamasını yapar.
8.Yüzey integralini mühendislik problemlerine uygular.
1, 3
Yrd. Doç. Dr. Mehmet MERDAN