Bileşik Olasılık Dağılım
Fonksiyonları
2
06.12.2016
3
06.12.2016
4
06.12.2016
• Örnek: Bir torbada 3 beyaz, 5 siyah top vardır. İadeli olarak arka arkaya iki top
çekiliyor. X rassal değişkeni birinci ve Y de ikinci çekiliş sonunda elde edilen topların
rengini göstersin.
06.12.2016
Ortak Olasılık Kütle Fonksiyonu
• a) Çekilen topların ortak olasılık fonksiyonunu bulunuz.
• b) Toplam olasılığın bir olduğunu gösteriniz.
5
06.12.2016
Ortak Olasılık Kütle Fonksiyonu
Ortak olasılık kütle fonksiyonu
6
Ortak Olasılık Kütle Fonksiyonu
Çözüm: Örnek uzayımız
S= { TTT, TTY, TYT, TYY, YYY, YYT, YTY, YTT}
Y rassal değişkeni paranın yazı ve tura gelmesini gösterdiğine göre 0,1,2 ve
3 değerlerini alır. X ve Y rassal değişkenlerinin ortak olasılık kütle
fonksiyonu şöyledir;
06.12.2016
Örnek: Bir para üç defa atılıyor. X rassal değişkeni ilk atışta para yazı ise 0
değerini, tura ise 1 değerini alıyor. Y rassal değişkeni ise gelen yazıların
değerini gösteriyor. Ortak olasılık dağılım fonksiyonunu yazınız.
7
06.12.2016
Örnek
8
9
06.12.2016
• Örnek: Bir istatistik enstitüsünde bulunan hesap makinelerinin
%40’ı elektrikli ve sağlam, %20’si elektrikli ama bozuk, %10’u elle
çalışıyor ve sağlam, %30’u elle çalışıyor ama bozuktur.
• a) Ortak olasılık fonksiyonunu oluşturunuz.
• b) Marjinal olasılık fonksiyonlarını bulunuz.
X RD’i elektrikli ise 1
elle çalışıyorsa 0 değerini,
06.12.2016
Marjinal olasılık fonksiyonları
Y RD’i elektrikli ise 1
elle çalışıyorsa 0 değerini,
10
06.12.2016
• b) Satır ve sütun toplamları marjinal olasılık fonksiyonunu
verdiğinden;
11
Marjinal Olasılık
06.12.2016
Örnek:
12
13
06.12.2016
06.12.2016
Örnek:
14
15
06.12.2016
06.12.2016
Sürekli R.D.
16
17
06.12.2016
18
06.12.2016
06.12.2016
Örnek
19
20
06.12.2016
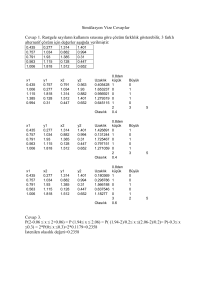
• Örnek: Bir torbada 3 beyaz, 5 siyah top vardır. İadeli olarak arka arkaya iki top
çekiliyor. X rassal değişkeni birinci ve Y de ikinci çekiliş sonunda elde edilen topların
rengini göstersin.
06.12.2016
Ortak Olasılık Kütle Fonksiyonu
• a) Çekilen topların ortak olasılık fonksiyonunu bulunuz.
• b) Toplam olasılığın bir olduğunu gösteriniz.
21
06.12.2016
Ortak Olasılık Kütle Fonksiyonu
Ortak olasılık kütle fonksiyonu
22
Ortak Olasılık Kütle Fonksiyonu
Çözüm: Örnek uzayımız
S= { TTT, TTY, TYT, TYY, YYY, YYT, YTY, YTT}
Y rassal değişkeni paranın yazı ve tura gelmesini gösterdiğine göre 0,1,2 ve
3 değerlerini alır. X ve Y rassal değişkenlerinin ortak olasılık kütle
fonksiyonu şöyledir;
06.12.2016
Örnek: Bir para üç defa atılıyor. X rassal değişkeni ilk atışta para yazı ise 0
değerini, tura ise 1 değerini alıyor. Y rassal değişkeni ise gelen yazıların
değerini gösteriyor. Ortak olasılık dağılım fonksiyonunu yazınız.
23
• Örnek: Bir istatistik enstitüsünde bulunan hesap makinelerinin
%40’ı elektrikli ve sağlam, %20’si elektrikli ama bozuk, %10’u elle
çalışıyor ve sağlam, %30’u elle çalışıyor ama bozuktur.
• a) Ortak olasılık fonksiyonunu oluşturunuz.
• b) Marjinal olasılık fonksiyonlarını bulunuz.
X RD’i elektrikli ise 1
elle çalışıyorsa 0 değerini,
06.12.2016
Marjinal olasılık fonksiyonları
Y RD’i elektrikli ise 1
elle çalışıyorsa 0 değerini,
24
06.12.2016
• b) Satır ve sütun toplamları marjinal olasılık fonksiyonunu
verdiğinden;
25
Marjinal Olasılık
06.12.2016
Örnek:
26
27
06.12.2016
06.12.2016
Örnek:
28
29
06.12.2016
06.12.2016
Örnek:
30
31
06.12.2016
06.12.2016
Örnek:
32