NORMAL OLASILIK DAĞILIMI Yrd. Doç. Dr. Esra KÜRÜM
30.10.2014 Normal olasılık dağılımı • İsta&s&kte en çok kullanılan dağılımdır. • Doğadaki çoğu sürekli rassal değişkenin bu dağılıma sahip olduğu varsayılır. • Çan şeklinde simetrik bir şekli vardır. • Tanım aralığı bütün reel sayılardır, -­‐ ∞<x<+∞. • Normal dağılım için μ=aritme&k ortalama=mod=medyan maNormal olasılık dağılımı mak üzere olasılık dağılım fonk.
erimine
sı µ ve
a sahiptir.
Prof.Dr.A.KARACABEY
σ
Normal olasılık dağılımı • X~N(μ,σ2) random variable is said to have a normal distribution with param
pdf of X is:
1
2
f (x : µ, ) = p
2⇡
as X ⇠ N(µ,
2
).
2
e
(x
µ)2
2 2
,
1<x <1
Standart normal olasılık dağılımı • Normal dağılımın aritme&k ortalaması μ=0 ve varyans σ2=1 ise bu dağılıma standart normal dağılım denir. • Bu dağılımın rassal değişkeni Z ile gösterilir. • Olasılık yoğunluk fonksiyonu, f(z) = Standart normal olasılık dağılımı ormal
fiği μ=0 a
iktir ve
ksene
olarak
ki tüm
ğundan o
sağ ve
an
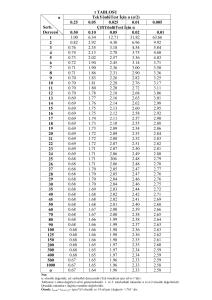
Standart normal tablolarının kullanımı • zα gösterimi • Tablodan z0.05 ve z0.033 değerlerini bulunuz. • P(Z<-­‐1.34) ve Z’nin 0.35’den büyük olma olasılıklarını bulunuz. • Tablodan ayrıca yüzdelikler de bulunabilir: 10. yüzdeliği ve 45. yüzdeliği bulunuz. • Normal dağılımlarda olasılıklar eşitsizlikler
Normal lasılık ddönüştürülerek
ağılımı yardımıylaointegrale
hesaplanır: yani,
Prof.Dr.A.KARACABEY
Doç.Dr.F.GÖKGÖZ
Normal ve Standart Normal Dağılım Normal dağılım gösteren X değişkeni aşağıdaki şekilde standart normal dağılan Z değişkenine dönüştürülmesi: Örnek • X, Türkiye'deki şirketlerin yıllık ithalat miktarını gösteren ortalaması 129 milyon dolar ve standart sapması 19.8 milyon dolar olan normal dağılım gösteren değişkendir. • Rastgele seçilen bir şirke&n yıllık ithalat miktarının 135 milyon dolardan fazla olma olasılığı nedir? • Rastgele seçilen bir şirke&n yıllık ithalat miktarının 120 milyon dolardan az olma olasılığı nedir? • Yapılan yıllık ithalat miktarının 90. ve 25. yüzdeliklerini hesaplayınız. Örnek • X~N(3,0.16) dağılıyorsa aşağıdaki olasılıkları hesaplayınız: • P(X>3) • P(2.8 ≤ X ≤ 3.1) • X’in 98. yüzdeliğini bulunuz. • c sayısını bulunuz: P(3-­‐c < X < 3+c) = 0.90. Örnek • Bir işletmede üre&len vidaların çaplarının uzunluğunun ortalaması 10 mm ve standart sapması 2 mm olan normal dağılıma uygun olduğu bilinmektedir. Buna göre rastgele seçilen bir vidanın uzunluğunun 8.9mm’den az olmasının olasılığını hesaplayınız.